The Weighted Path Order for Termination of Term Rewriting

 プログラムが暴走するというのは，もっとも典型的な不具合のひとつである．

 そこで，任意の入力に対して暴走せず出力を返すこと，すなわちプログラムの「停止性」を保障することが重要である．特に，関数型プログラムのモデルとされる「項書換え系」において，停止性を保障する研究が進んでいる．これまでに多くの停止性自動証明ツールが開発され，毎年国際競技会が開催されているほどである．近年では，C, Java, Haskell，Prologなど，実用的なプログラミング言語を項書換え系に変換して停止性証明を行う研究がなされ，実用規模のプログラムの検証に耐えるスケーラブルな停止性証明ツールが以前にも増して求められるようになっている．

 そこで本研究は，項書換え系の強力な停止性証明法の提案とその効率的な実装に取り組んだ．

 項書換え系の停止性証明の基本は，書換えが起こるたびに減少する「順序」を発見することである．1970年初頭から現在に至るまで，このような順序が数多く提案されてきた．これらはそれぞれ異なる論理によって正当性が示され，それぞれ異なる実装を必要としていた．本研究では，既存手法に共通する本質を抜き出し，新たな停止性証明法である「重み付き経路順序」を提案した．

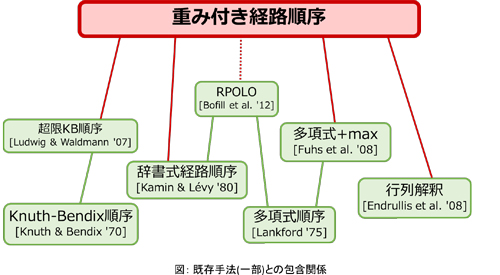
 提案手法は，多くの既存手法を実装可能な形で包含し，また真に強力になっていることを理論・実験両面から示した．これにより，登場以来およそ40年間統合されることのなかった，Knuth-Bendix順序，多項式順序，辞書式経路順序などの著名な既存手法を統合することに成功した．

 また近年の停止性証明ツールは上記基本手法を適用する際，引数の「切り落とし」および「並び替え」を行っている．本研究ではこれらを融合し，従来手法では切り落とされていた引数の情報（重み）を用いることで停止性証明能力が有意に向上することを示した．

 提案手法の実装法として，算術論理上の充足可能性（SMT）ソルバを効率的に用いた手法を提案し，停止性証明ツール Nagoya Termination Tool（NaTT）として実装した．停止性証明ツールの世界競技会 Termination Competition 2014 に参加し，NaTTは項書換え系（standard）カテゴリにて出場5ツール中2位の証明能力を示し，効率面においては他のツールの約5倍の効率化を実現した．またNaTTはこれまで停止性が判明していなかったベンチマーク159問のうち，36問の停止性（及び1問の非停止性）を明らかにした．