GPU Parallelization of Cryptographic Primitives using Multivariate Quadratic Polynomials and its Security Evaluation

 ストリーム暗号はメッセージの暗号化に用いる鍵に疑似乱数の結果を利用する暗号方式である．この暗号方式で利用する疑似乱数は，通常，処理時間が短く，かつ，軽量であり，撹拌性能が高いものが選択される．また，メッセージの暗号化においても，メッセージと鍵との排他的論理和で暗号化を行うため，高速，かつ，軽量である．従って，ストリーム暗号は他の方式と比較して，高速で軽量な暗号方式であることが知られている．一方で，ストリーム暗号の安全性は，主に，既知の攻撃手法に対して評価されており，それらの攻撃に対して，安全であることは保証されているものの，将来的には，その暗号に対して効率的に解読可能な手法が開発されることによって安全性が急激に低下する可能性が存在する．そこで，公開鍵暗号方式と同様に，安全性の根拠に既知の解決困難な数学の問題を利用する種類のストリーム暗号の開発が行われている．この種の暗号では，暗号解読の困難性，すなわち，暗号の安全性を，対象の暗号が利用する数学問題の解決困難性に帰着することを証明できる．すなわち，これらの数学問題を解決するために必要な計算時間を，利用している暗号の解読に必要な計算時間の指標とすることが可能である．そのため，将来的な安全性の推移を評価することが可能である．

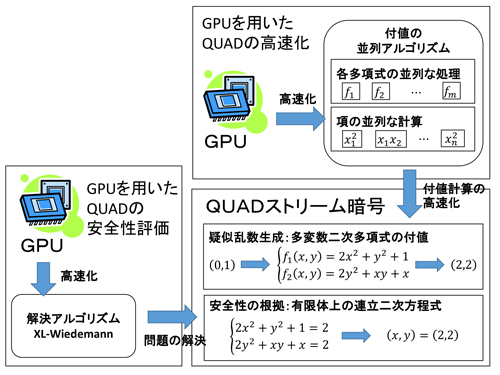
 本研究では，QUADと呼ばれる安全性の証明可能なストリーム暗号を実用化するために，QUADに関連するアルゴリズムをGPUを用いて並列化し，高速化を図った．QUADは，疑似乱数の生成に有限体上の多変数二次多項式の付値を利用しており，安全性の根拠として，有限体上の連立二次方程式の求解問題（MQ問題）の解決困難性を利用した暗号である．QUADの課題点は大きく3つ存在する．（1）疑似乱数の生成に多変数二次多項式の付値を利用しているため，多数の加算及び乗算の処理が必要となり，他のストリーム暗号と比較して計算コストが大きい．（2）多変数二次多項式内 のすべての係数を保存しなければならないため，大量のメモリ領域を必要としている．（3）QUADの将来的な安全性に関して，十分に評価されているとは言えない．本研究ではこれらの課題点の内，（1）及び（3）の解決を図った．

 具体的な本研究の貢献は，以下の通りである．