(邦訳:線形相補性問題:計算複雑度と整数性)
| 澄田 範奈 国立情報学研究所 特任研究員 |
[背景]数理計画法における線形相補性問題の理論的・実用的重要性
[問題]線形相補性問題の計算複雑度の解析と整数解の存在性
[貢献]線形相補性問題の疎性に関する計算複雑度の分類と,整数性を議論する枠組みの提案
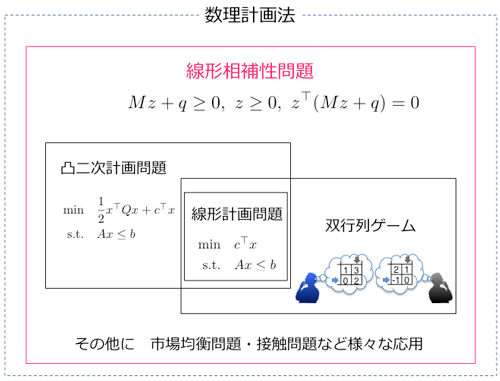
数理計画法では,数理モデル上で何らかの条件を満たす解を効率良く計算する方法が研究課題である.たとえば,現在地から目的地まで行く最短の経路や,予算内で栄養基準を満たす献立を計算する問題を扱う.この分野は1950年代から,計算機の性能向上とともに急速に発展してきた.基本的な問題である線形計画問題(線形不等式系を満たす中で線形関数を最大・最小にするベクトルを求める問題)や凸二次計画問題は特によく研究され,効率の良いアルゴリズムをもつことが知られている.1960年代には,これらの問題と,ゲーム理論で基本的なモデルである双行列ゲームを一般化した問題として,線形相補性問題と呼ばれる問題が導入された.線形相補性問題は,線形不等式系と相補性条件を満たすベクトルを求める問題である.相補性条件をもつことにより,線形相補性問題は経済学の市場均衡問題や力学の接触問題などさまざまな問題を表現できる.そのため,線形相補性問題は応用・実用上も重要な問題である.
本研究では,線形相補性問題の計算複雑度(計算にかかるコストの理論的評価)と整数性(整数ベクトルの解の存在性)の研究を以下のように行った.
(1)計算複雑度
線形相補性問題はNP困難と呼ばれる難しい問題であることが知られている.その一方で,応用上現れる線形相補性問題は係数行列に何らかの性質をもつことが多いため,行列の性質を仮定した上で計算複雑度の解析が盛んに行われている.
本研究では,係数行列の各行がもつ非ゼロ要素数,つまりある種の疎性に応じた計算複雑度の分類を行った.多項式時間可解,すなわち効率良く解けるクラスには,現状で最速のアルゴリズムを与えた.問題のもつ疎性は,線形相補性問題の特殊ケースである線形不等式系や双行列ゲームのアルゴリズムでも利用されている.
さらに,係数行列や解ベクトルの疎性をパラメータとして,線形相補性問題のパラメータ化計算量の解析も行った.また,線形相補性問題の解の中で特定の形のものを見つける「方向つき線形相補性問題」を導入し,行列クラスによる計算複雑度を解析した.
(2)整数性
線形相補性問題に整数解が存在するための十分条件には,係数行列の主単模性がかかわることが知られている.一方,線形計画問題では,整数最適解が存在するための十分条件として,係数行列の完全単模性と,これを弱めた概念である線形不等式系の完全双対整数性が知られている.本研究では,上で触れた方向つき線形相補性問題を用いて線形相補性問題の「双対性」を定義し,線形計画問題との類推により線形相補性問題の完全双対整数性を導入した.その上で,線形計画問題で知られている結果と類似の結果を示した.
(2015年6月15日受付)

