秘密計算を用いた顔認証の構成について
A Study on Privacy-Preserving Face Authentication with Secure Computation
1. 序論
1.1 背景
近年,深層ニューラルネットワークを用いた画像認識性能の向上に伴い,顔画像を利用した認証の精度が上がり,多くの場面で活用されるようになってきた.たとえば,アミューズメント施設やイベント会場への入場時の本人確認などに顔認証が利用されており,非接触な認証として利用が広まっている[1].しかし,顔画像は生体情報の一種で個人を特定するのに十分な情報であり,また,生涯不変な情報であることから,漏えいしたときに大きな被害をもたらす可能性がある[2].このため,情報が漏えいしたとしても利用者への被害を抑えられるように,システム内においても秘匿されることが望ましい[3].
一般に,被認証者が顔認証システムを利用する際にはあらかじめシステムのデータベースに顔画像を保存しておき,認証する際に入力された顔画像と機械学習を用いて比較し,認証する[4].認証結果として,入力された顔画像の人物がシステムに登録されているか否か出力される.このとき,認証に際して入力された顔画像やデータベース内に登録されている顔画像から被認証者の情報が洩れることに加え,認証結果から誰がシステムに登録されているかが分かってしまう.したがって,被認証者の顔画像をシステムのデータベースと認証の際の入出力双方の観点から秘匿する必要がある.そのような高い安全性をもつ顔認証は,データを秘匿化した状態で任意の関数を評価する秘密計算を用いることで実現が期待できる.このような顔認証を本稿では秘匿顔認証と呼称する.このとき,前述したとおり,入力された顔画像,顔画像データベース,および,認証結果が認証者と被認証者以外(DBサーバの管理者,認証システム提供者など)から秘匿化される.
本稿では,顔画像の比較に機械学習,顔画像の秘匿に秘密計算を用いた1対1秘匿顔認証を設計する.ここでいう1対1とは,被認証者が顔画像を入力する際に自らのIDを提示することで,本当にそのIDを持つ人物の顔画像か確認する設定である.大まかには機械学習により顔画像の特徴量を抽出し,その特徴量を秘密計算で秘匿した状態で,データベース上に保存された特徴量との統計的距離を計算する.
本稿における貢献は,上述した設定において,秘密計算に適した特徴量の形式および特徴量間の統計的距離の計算方法を,計算時間と認証精度双方の観点から実験的に明らかにすることである.一般的な機械学習では浮動小数点演算を用いる一方,秘密計算を用いた推論処理の既存研究[5]–[16]では秘密計算の剰余演算により計算結果に誤差が生じること[17]に加え,計算時間の大幅な増加が起こりえる[10].このため,上述した既存研究では精度と計算時間を改善するために,入力を固定小数点に変換していた.これに対し,本稿では特徴量の抽出にArcFace [18],秘密計算にEzPC [19], ABY3 [11]のいずれかを用いてそれぞれ実装し,特徴量の形式を浮動小数点あるいは固定小数点として実験を行った.その結果として,主な貢献として3つの知見を得た.
まず1つ目の知見として,認証にかかる計算時間と認証精度の双方の観点から最も優れた設定は,特徴量の形式が整数値かつ特徴量間の統計的距離の計算方法がコサイン類似度であることを確認した.実装した設定としては,特徴量の形式が実数値あるいは整数値のときに特徴量間の統計的距離の計算方法としてコサイン類似度あるいはユークリッド距離のそれぞれを用いた4とおりの設定と,特徴量の形式がバイナリ値のときに統計的距離の計算方法としてハミング距離を用いた.このとき,特徴量の形式がバイナリ値の場合,整数シェアに加えてバイナリシェアを用いることが考えられることから,それぞれのシェアを用いてハミング距離を計算するため2とおりの設定を実装した.したがって,この知見は計6とおりの設定を実装して,それぞれの認証にかかる計算時間と認証精度を測定して得られた知見である.
次に2つ目の知見として,1対1秘匿顔認証においては特徴量の形式として浮動小数点を用いたとしても,既存の秘密計算ライブラリであるEzPC [20]を用いることで,(秘密計算を用いない)従来の顔認証と比べて精度の劣化なく,実用十分に高速な構成が可能なことを確認したことである.従来の顔認証では特徴量の形式として実数値,かつ,特徴量間の統計的距離の計算方法としてコサイン類似度を用いていた.一方,上述したとおり,秘密計算を用いた生体認証では特徴量を固定小数点化することが前提であり,主に秘密計算ライブラリの内部処理を通じて固定小数点化されていた[11].このため,筆者の知る限り,従来の顔認証と厳密に同じ設定は,秘匿顔認証では利用されてこなかった.これに対し,特徴量の形式を浮動小数点のまま秘密計算を実行するEzPCを用いたところ,95%以上の認証精度かつ0.2秒以内の認証計算時間を達成した.直観的には,これまで有効な設定として用いられてた入力の固定小数点への変換が,秘匿顔認証における精度と計算時間の改善に必ずしも必要ではないことが確認できたことを意味している.
3つ目の知見として,入力となる特徴量の形式の固定小数点への変換においては,特徴量をバイナリ値にするより,整数値にすることで精度が高く,かつ,認証計算時間が短くなることを示したことである.とくに特徴量の次元数を増やしたときに,本稿で用いたいずれの秘密計算ライブラリ[11], [20]においても,この傾向は顕著だった.これはバイナリ値を論理演算可能なシェアにした場合,計算の過程でシェアの変換が必要であり,次元数を増やしたことで相対的に計算量が増加したためである.上述した知見は,特徴量の形式を固定小数点に変換した際の,秘匿顔認証の精度と認証計算時間への影響を詳細に分析した点に価値がある.
本稿の貢献を要約すると,以下のとおりである:
- ・1対1秘匿顔認証を設計し,秘密計算に適した特徴量の形式および特徴量間の統計的距離の計算方法を実験評価したところ,認証にかかる時間と認証精度の双方の観点から最も優れていた設定は,特徴量の形式が整数値かつ統計的距離の計算方法がコサイン類似度のときであった.
- ・秘密計算の設定には固定小数点が好ましいとされていたが,特徴量の形式として浮動小数点を用いたとしても,実用上充分に高速な1対1秘匿顔認証構成が可能である.浮動小数点を用いることは,従来の1対1顔認証と同じ設定である.
- ・特徴量の形式を固定小数点に変換する際は,バイナリ値よりも整数値のほうが精度が高く,かつ,高速に計算可能である.
2. 関連研究
本章では関連研究として,秘匿顔認証,秘匿生体認証,および一般的な秘匿推論について紹介する.
2.1 秘匿顔認証
秘匿顔認証は入力となる画像レベルで加工する手法と,秘密計算を通じて顔画像の表現自体を変換する手法に大別される[21].以下にそれぞれ詳細を述べる.
まず画像レベルでの加工処理には顔の部分に対するマスキング[22]–[24],顔のフィルタリング[25]–[27],および顔画像へのモザイクなど画像変換[28]–[30]する方法が知られている.しかし,これらの方法では理論的な安全性の保証を与えることは難しい.差分プライバシーに基づく顔認証[31]–[33]は理論的な安全性の保証もできるが,差分プライバシーは一般に推論時の秘匿が不十分である[5].このため,秘密計算を用いた手法が望ましいといえる.
秘密計算を通じて顔画像の表現自体を変換する手法は準同型暗号を用いた手法が主流である[34]–[36].また,準同型暗号とガーブル回路[37]を組み合わせた手法もある[38], [39].これらの方式の主な動機はデータベースに保存された顔画像テンプレートの保護である[34].近年では準同型暗号の導入に向けて特徴量を整数化する手法が議論されている[40], [41].一方,計算量の削減としてはバイナリ値とハミング距離が注目されていた[35].とくに近年では深層学習とハミング距離を組み合わせた手法もある[4].しかし,一般に準同型暗号では計算時間の観点で秘密分散に劣る[42].このため,本稿では秘密分散を用いた手法を検討する.近年ではキャンセラブルバイオメトリクスと秘密分散を融合した方式[43]も知られており,本稿ではこの方式と比較検討を行う.
2.2 秘匿生体認証
生体認証の秘匿化は一般にキャンセラブルバイオメトリクスと秘密計算を用いた認証に大別される[44].キャンセラブルバイオメトリクスでは生体情報の特徴量に対して不可逆の変換を施すことで,生体情報が秘匿化できる[2].しかし,不可逆変換ゆえに元となる生体情報が欠落した際に修復不可能であるという課題が指摘されている[45].秘密計算を用いた手法では準同型暗号[46]を用いた指紋認証方式が提案されている[47], [48].一般には顔画像のほうがソーシャルネットワークにおいて利用されるなど,ユースケースが豊富かつプライバシーの懸念が指摘されている[21].
2.3 秘匿推論
秘密計算を用いた汎用的な推論処理[5]において,推論処理に加え機械学習モデルも保護するプロトコルが知られている[6]–[16].データベースをモデルとして考えた際に,これらのプロトコルは本稿の議論に近い技術といえる.上述したプロトコルは任意のタスクを想定した汎用的な秘匿推論処理を議論する一方,顔認証のように複雑な特徴量を高速に処理するアプリケーションにはしばしば不向きであることが予想される.これに対し,本稿では顔認証に特化したプロトコルを設計することで,上述したプロトコルよりも高速な処理が期待できる.なお,多くの秘匿推論の既存研究[5], [49]–[60]はモデルの保護(本稿におけるデータベースに相当)を対象としていない.
3. 秘匿顔認証
本稿では秘匿顔認証のうち,1対1顔認証と呼ばれるものを提案する.以下では1対1顔認証を導入したのち,秘匿顔認証のための要件を整理する.それから,本稿の問題設定を述べる.
3.1 顔認証
顔認証は大まかに特徴量抽出器とデータベースという2種類のエンティティから構成される.特徴量抽出器とは,与えられた顔画像からその特徴量を求め出力することで,顔認証の入力インタフェースとしての役割を果たす.データベースには顔画像の特徴量が登録されており,特徴量抽出器から受け取った特徴量を登録されている特徴量と突合し,認証を行う.データベースはサーバ上に実装されるものであるが,一般にサーバが複数存在することが考えられる.これにはデータベースに冗長性を持たせる,あるいは,データを分割してセキュリティを高めるなど様々な目的が考えられるが,いずれにせよこのような場合はサーバ間で通信を行うことが必要となる.
顔認証の処理は通常,登録と認証の2段階に分けられる.登録段階では認証したい人物の顔画像の特徴量を抽出し,データベースに登録する.認証段階では,特徴量抽出器から受け取った特徴量とデータベースに登録されている特徴量とを比較し,この被認証者が登録されているかどうかを判定する.最後に認証結果が被認証者に送付され,実行完了となる.
本稿ではとくに1対1顔認証を扱う.1対1顔認証とは,認証に被認証者ごとに固有のIDを用いる方式である.登録段階では顔画像のみならず該当する人物の被認証者IDを登録し,これらを紐づける.認証の際には被認証者の顔画像と被認証者IDを入力する.与えられた被認証者IDを基に,このIDと紐づけて登録されている顔画像と今入力されている顔画像とを比較し,同一人物であるか判定を行う.このように登録されている全ての顔画像と比較するのでなく,被認証者IDによってデータベースの探索範囲があらかじめ限定されている点が1対1顔認証の特徴である.なお,他方で被認証者IDのような紐付け用の情報を用いずに,データベースに登録された複数の候補と認証用の顔画像を比較して認証を行う手法を1対N顔認証と呼ぶ.1対N認証は今後の課題である.
3.2 秘匿顔認証の要件
3.2.1 守るべき情報
まず秘匿顔認証で守るべき情報は何かを述べる.1.1節で述べたとおり,秘匿顔認証では被認証者のプライバシ情報である顔画像とその特徴量を含む情報を認証者と被認証者以外(DBサーバの管理者,認証システム提供者など)から秘匿することを目的とする.特に本稿では,データベースサーバが汚染されるような状況を想定し,そのような場合であっても安全な秘匿顔認証を考える.したがって,秘匿化する必要があるものは,顔画像を含む入力情報と,データベースに登録されている情報である.さらに,認証した人物や認証結果の記録が必要な場合は,出力の認証結果も秘匿されるべきである.そのようなアプリケーションの例として入退室管理が挙げられる.入退室管理などでは誰が利用したかを記録する必要があるので,認証結果には認証の可否に加え,認証された人物の情報,被認証者のIDまたは顔画像が含まれる.このため,認証結果も秘匿することを考える.
3.2.2 攻撃者のモデル
本稿では複数存在するデータベースサーバが結託したとしても上述の情報を秘匿できる秘匿顔認証方式を提案する.ただしすべてのサーバが結託した場合情報を秘匿することは原理的に困難であるため,少なくとも1台のサーバは正常な状態であるとする.また,本稿では顔認証のうち特に認証段階における攻撃を考える.したがって顔画像の登録は正常に行われるものとする.
冗長性を持たせるために複数台のサーバが存在する場合は,すべてのサーバでデータが同期されているため1台でもサーバが汚染されると情報漏洩の恐れがある.したがって,本稿で考える攻撃者のモデルは,セキュリティを高めるために複数のサーバが用意されている場合を前提としている.
3.3 秘匿顔認証の概要
秘匿顔認証の構成に関しては既存研究[4]に従うものとする.具体的には,顔画像を取得するカメラに特徴量抽出器を搭載し,特徴量抽出を行う.そして,得られた特徴量を各サーバに送信する.このとき,特徴量抽出器を秘匿化すると特徴量抽出に時間がかかってしまうことから,特徴量抽出器は秘匿していない.カメラで得られる顔画像とその特徴量はカメラに保存しないことで,カメラからの情報漏洩を防ぐ.ここで使用するカメラは被認証者もしくは認証者の管理下にあるものとする.顔画像から特徴量抽出の際には,顔画像・特徴量を保存しないためカメラはいずれの管理下でも安全性には影響しない.その概念図を図1に示す.
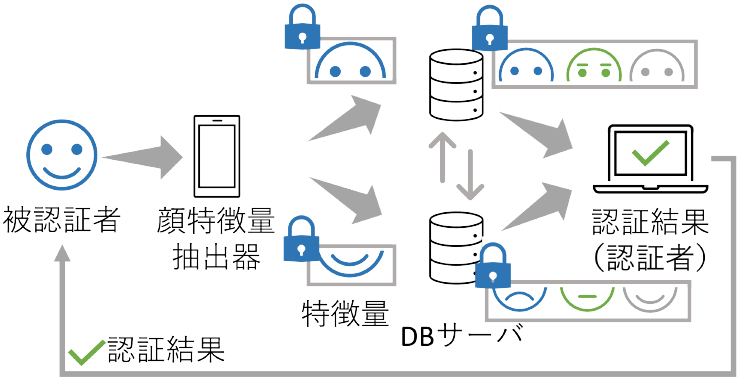
Fig. 1 System configuration.
また,特にサーバが汚染された場合でも顔画像が漏洩しない秘匿顔認証アルゴリズムの構築を目標とし,公開された通信路を流れる入出力情報の保護は考慮しないものとする.なぜならば,これらの情報はTLSなどの暗号化通信技術を用いることで保護することが可能なためである.なお,機械学習モデルへの攻撃としては学習データを推論出力を通じて復元する攻撃[61]や,機械学習モデルそのものを得る攻撃[62]が考えられるが,これらの攻撃は本稿の対象外とする.これらの攻撃は学習時における差分プライバシーの適用[63], [64],あるいは機械学習モデルへの電子透かし[65]が有効である.これらの手法は,後述する提案手法と平行して運用が可能である.
3.4 本稿の問題設定
本稿では秘密分散ベース秘密計算と機械学習を組み合わせた秘匿顔認証を提案する.その特徴は,入力される顔画像,顔画像データベース,および認証結果を秘匿可能な点である.表1に示すとおり,入力される顔画像,顔画像データベース,認証結果すべてを秘匿する手法は提案手法のみである.なお,提案手法の特徴量と統計的距離に表記されている“★”は,様々な設定を許容することを意味する.
Table 1 Settings of existing privacy-preserving face authentication.
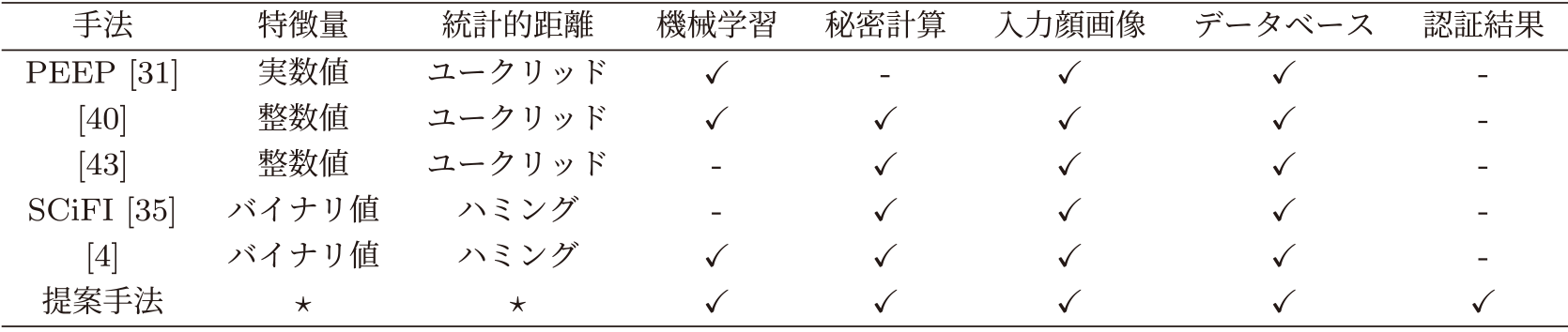
本稿の主な問題設定は,提案手法を実装することで,機械学習として以下に述べるような秘匿顔認証に適した設定を明らかにする.また,その実行速度が実用的であるかについても実験的に明らかにする.(実験の詳細は5章,その考察は6章を参照されたい.)ここで言う機械学習の設定とは,特徴量としてのベクトルの設定(実数値・整数値・バイナリ値)と,特徴量を比較する際の統計的距離の形式(コサイン類似度・ユークリッド距離・ハミング距離)を意味する.これらはいずれも機械学習において広く用いられている設定であるが,筆者らの知る限り,秘匿顔認証においてこれらの設定を調査した既存研究は存在しない.表1に機械学習あるいは秘密計算を用いた秘匿顔認証に関する各文献の設定を示す.特筆すべき点として,特徴量間の統計的距離の計算方法としてコサイン類似度を用いることは機械学習において一般的であるものの,筆者らの知る限り,既存の秘匿顔認証の文脈でそのような構成を用いているものは示されてこなかった.このため,上述した特徴量間の形式および特徴量間の統計的距離の計算方法を,秘匿顔認証の実装評価を通じて包括的に検討する.これにより,秘匿顔認証に適した設定を明らかにする.なお,秘密計算の実装については広く用いられているライブラリであるABY3 [11], EzPC [20]をそれぞれ用いることで,これらの違いが秘匿顔認証の実行速度にどのように影響するかを明らかにする.
4. 提案手法
本章では提案手法を述べる.まずは構成要素を含む全体像を述べたのち,アルゴリズムの詳細,ならびに,実装を含めた実際の構成を述べる.
4.1 全体像
本稿で提案する秘匿顔認証は顔認証アルゴリズムと秘密分散ベース秘密計算を構成要素とする.これらの構成要素を用いて,秘匿顔認証における顔画像登録,特徴量抽出,顔認証の各機能を実現する.本節ではこれらの構成要素を説明したのち,提案する秘匿顔認証の全体像を示す.
4.1.1 構成要素の説明
以下ではあるアルゴリズム$X$のサブルーチン$A$を$X.A$と表すことにする.まず提案方式の前提として,(秘匿化されていない)顔認証アルゴリズム$FR$はサブルーチンとして顔登録機能$FR.Reg$,特徴量抽出器$FR.FtrExt$,顔認証機能$FR.FaceRcg$が存在するものとする*1.データベースに顔画像を登録する際には,$FR.FtrExt$で抽出した特徴量が用いられる.顔認証の際は入力された顔画像から特徴量を抽出したのちデータベースと照合し,認証成功/失敗を判定する.
次に,本稿で扱う秘密分散ベース秘密計算$SC$はサブルーチンとしてシェア生成機能$SC.Share$と評価関数$SC.Eval$を持つ[66], [67].シェアとは秘匿したい情報を何らかの形で分割したものである.ある定められた組み合わせを集めると元の情報が復元できる一方,シェア単体からは情報が復元できないという性質を持つ.評価関数は複数のシェアを入力したときに,シェアが定められた条件を満たすならば元の秘匿したい情報を明かすことなく所望する計算を行えるという性質を持つ.現在の秘密分散ベース秘密計算では任意の演算に対する秘密計算が可能である[68]–[70].また,本稿では特に秘密計算の性質として秘匿推論を求める.すなわち,秘密計算に参加した各エンティティには計算結果のシェアのみが出力として与えられるとする.
4.1.2 全体像の説明
本稿で提案する秘匿顔認証では,一人の被認証者(クライアント)とn台のサーバの間で顔認証を行う.サーバにはあらかじめ顔画像の特徴量(と被認証者ID)を登録しておく必要があるが,顔画像の特徴量はn個のシェアに分割されており,各サーバには被認証者IDに紐づく1つのシェアが与えられている.顔認証の際には特徴量抽出器に被認証者IDと顔画像を入力として与える.その結果として得られる特徴量はn個のシェアとして分割され,各サーバに分配される.各サーバはあらかじめ登録されたシェアと分配されたシェアを用いてサーバ間で秘密計算を行う.この際の秘密計算は分配されたシェアと登録されたシェア間の統計的距離の計算を行い,あるしきい値d以上の値が得られた場合は認証成功を,そうでなければ認証失敗を出力する.認証結果は各サーバにシェアとして分配され,各サーバから被認証者へ出力結果のシェアを送付する.以上のように各サーバに与えられる情報は(被認証者IDと)シェアのみであるため,各サーバが顔情報や認証結果を復元することはできず,秘匿顔認証が実現できる.
4.2 アルゴリズムの詳細
秘匿顔認証のアルゴリズムの詳細を以下に示す.まず,(秘匿化されない)顔認証アルゴリズム$FR = (Reg,FtrExt,FaceRcg)$と秘密分散ベース秘密計算$SC = (Share,Eval)$を用いた秘匿顔認証アルゴリズム$SFR = (Reg,FtrExt,FaceRcg)$の構成を図2に示す.ここで,サーバはn台あるものとする.以下に各機能の詳細を述べる.

Fig. 2 Configuration of privacy-preserving face authentication algorithm SFR.
顔登録機能$SFR.Reg$は識別子idと顔画像Pictを入力とし,以下のように動作する.初めにPictを特徴量抽出器$FR.FtrExt$に入力し,特徴量Xidを得る.一般に特徴量はベクトルとして表現される点に留意されたい.さらにXidに対するシェアをシェア生成機能$SC.Share$を用いて求め,シェア$X_1^{id}$, …, $X_n^{id}$を得る.最後にi = 1, …, nに対して$DB_i^{id}: = (id,X_i^{id})$とし,これらを出力する.ここで$DB_i^{id}$はサーバiに保存される,識別子idとそれに紐づく顔画像の特徴量に関するシェアである.
特徴量抽出器$SFR.FtrExt$は$SFR.Reg$と非常によく似た動作をする.識別子idと顔画像Faceを与えられると,$SFR.FtrExt$同様シェアx1, …, xnを求め,idとともに出力する.ここでxiはサーバiに分配されるシェアである.
顔認証$SFR.FaceRcg$は入力としてid, ${\{ DB_i^{id}\} _{i \in [n]}}$, ${\{ {x_i}\} _{i \in [n]}}$が与えられる.これは各サーバがそれぞれの入力を用いて計算を実行するという意味であり,1つのアルゴリズムに全てのシェアが入力として与えられるわけではないことに注意されたい*2秘密計算${\{ {y_i}\} _{i \in [n]}}$←$SC.Eval$$({({x_i})_{i \in [n]}},{(X_i^{id})_{i \in [n]}})$を実行し,その結果を出力する.ここで,yiは各サーバが得る認証結果のシェアであり,各サーバがそれぞれのシェアをクライアントに送付することで,クライアントのみが最終的な顔認証の結果を得られる.
4.3 実際の構成
本稿の秘匿顔認証の実装について以下に示す.実装は1台の特徴量抽出器と2台のデータサーバを用いる.つまり,n = 2の場合で実験を行っている.特徴量抽出器は機械学習としてArcFace [18]を用いて実装している.また,特徴量の形式として実数値,整数値,バイナリ値(ハッシュ値)をそれぞれを用いることが可能である.秘密計算にはEzPC [20], ABY3 [11]を用いている.秘密計算における特徴量間の統計的距離の計算にはコサイン類似度,ハミング距離,あるいはユークリッド距離のいずれかを用いる.
5. 実験
本章では提案手法について,実験評価の内容を述べる.まず実験目的を述べたのち,データセットとベースラインを含む実験設定を述べる.次に,計算時間と認証精度に関する実験結果を示す.
5.1 実験目的
本実験では前述した秘匿顔認証について,その計算時間と認証精度の観点から,秘密計算に適した特徴量の形式と統計的距離の計算方法を明らかにする.特に,実際の利用を考えた際にはモデルの訓練として用いるデータセットに顔画像が含まれていないような被認証者のシステムも考えられることから,訓練データを持たないような被認証者の認証についても確認する必要がある.なお,本稿では機械学習の設定の違いとして以下に述べる2つの観点,すなわち特徴量の形式と特徴量間の統計的距離の計算に着目して検討する.
まず特徴量の形式について,特徴量には浮動小数点として実数値,固定小数点として整数値とバイナリ値をそれぞれ用いる.実数値は一般に精度を得やすく機械学習で良く用いられる一方,整数値は剰余演算を伴う秘密計算との親和性が高い[8], [71].バイナリ値は値域を極小化した整数値であり,機械学習では次元削減[72]や計算速度の改善[73]に用いられるほか,秘密計算への応用も知られている[10], [56], [59].
次に,特徴量間の統計的距離の計算にはコサイン類似度,ハミング距離,あるいはユークリッド距離のいずれかを用いる.それぞれの計算方法は5.2.3節で述べるが,コサイン類似度はArcFace [18]をはじめ機械学習による画像認識で広く用いられている[72], [74].一方,ハミング距離は秘密計算を用いた顔認証において,計算量削減に用いられている[35].ユークリッド距離は機械学習と秘密計算いずれにもよらないような一般的な統計距離として用いる.上述した特徴量と統計的距離の計算から,秘匿顔認証における計算時間と認証精度を議論する.
5.2 実験設定
5.2.1 実装環境
各実装は4.3節で述べたとおり,特徴量抽出器にはArcFace [18],秘密計算の実装にはABY3 [11], EzPC [20]を用いて行った.秘匿顔認証全体はPyTorch [75]で実装している.特徴量抽出器のネットワークにはResNet50 [76]を使用している.それぞれのライブラリの情報を表2に,特徴量抽出器とデータベースサーバそれぞれの実装環境を表3と表4に記す.なお,ArcFace, ABY3とEzPCは開発者がバージョン管理を明示的に行っていないため,GitHubのURLのみ脚注に記載する*3,*4,*5. 4.3節で述べたとおりデータベースサーバ2台の構成を考えており,これらは同じ地域にある同種のAWSインスタンスを2つ用いることで実装されている.
Table 2 Software libraries used in implementation.
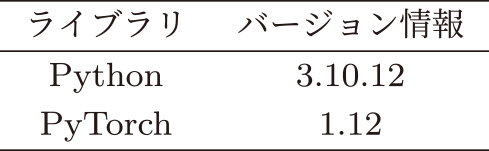
Table 3 Implementation environment of feature extractor.

Table 4 Implementation environment of database server.

5.2.2 データセットとベースライン
本実験では特徴量抽出器の訓練とモデルの評価にそれぞれ異なるデータセットを利用する.これは訓練データが十分にないような被認証者の顔画像も正確に認証できるか評価するためである.
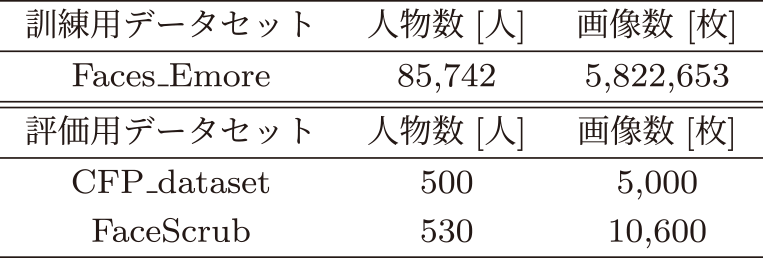
表5に訓練用データセットと評価用データセットを記す.特徴量抽出器の訓練には,Faces_Emoreデータセットを利用した.評価用データセットには,CFP_dataset [77]とFaceScrub [78]を用いている.具体的には,各人物の画像がCFP_datasetには10枚ずつ,FaceScrubには20枚ずつあることから,それらのうち3割の画像をしきい値の計算,残りの7割を精度と計算時間の評価にそれぞれ用いた.なお,ベースラインには秘匿化していないArcFace [18]を用いる.その目的関数は以下である.\[L = - \frac{1}{N}\sum\limits_{i = 1}^N {\log } \frac{{{e^{s(cos({\theta _{{y_i}}} + m))}}}}{{{e^{s(cos({\theta _{{y_i}}} + m))}} + \sum\limits\textstyle_{j = 1,j \ne {y_i}}^n {{e^{s\ \cos {\theta _j}}}} }}\]
Table 5 Datasets.
5.2.3 特徴量の形式と統計的距離の計算
本稿の実験では,特徴量は128次元,256次元,512次元のベクトルで表される.このとき,特徴量の形式を実数値,整数値,バイナリ値とした場合それぞれについて検討する.ここで,実数値はPyTorchライブラリの標準的な型である$float32$型で表現される値である.一方,整数値とバイナリ値はこの$float32$型の値を,それぞれ26倍してから−1した値の整数部だけを取り出すこと,あるいは,2で割った商を計算することで表現される.これらの計算について表6に示す.ここで,表中のxは実数値における特徴量(すなわち$float32$の値に相当)を意味する.ベースラインでは特徴量の形式を実数値とするモデルを用いる.なお,ABY3, EzPCにより生成されるシェアには整数シェアとバイナリシェアの2種類があるため,それぞれに合わせて特徴量の形式を整数値にしたモデルとバイナリ値にしたモデルを作成している.ここでいうバイナリシェアとは論理演算が可能なシェアであり,以降でバイナリ値の特徴量を論理演算するためにシェアにしたものをバイナリシェアと呼ぶ.前述したとおり,認証の際の特徴量間の統計的距離の計算ではコサイン類似度,ハミング距離,ユークリッド距離を比較する.コサイン類似度は2つのベクトルがどれほど似ているかを表す尺度であり,2つのベクトルがなす角のコサイン値で表現される.ハミング距離は,2つのベクトル間で値が異なる要素の数を示す値である.ユークリッド距離は,2つのベクトルを点と捉えたときの直線距離を表す尺度であり,ベクトル間の差の二乗和で表現される.
Table 6 Calculation methods in each feature format.

特徴量の抽出と特徴量間の統計的距離の計算において,ハミング距離は特徴量の形式がバイナリ値の場合のみ計算できる.一方ユークリッド距離をバイナリ値で計算すると,その計算方法から結果がハミング距離に一致する.また,バイナリ値でコサイン類似度を計算する場合,割り算が必要となる.しかし,一般に割り算は逆元が必要となり,計算負荷が高くなることから,割り算は避けることが望ましい.以上を踏まえ,実数値と整数値ではコサイン類似度とユークリッド距離を,バイナリ値ではハミング距離をそれぞれ計算する.バイナリ値ではシェアを整数シェアとバイナリシェアのそれぞれを用いてハミング距離を計算する.計算時間と認証精度は5,000回の試行の平均を測定した.なお,計算時間については,特徴量の抽出と認証における統計的距離の計算をそれぞれ計測する.
5.3 実験結果
本提案手法では,大きく2つの計算が行われるため,それぞれの計算にかかる時間を測定する.1つ目が特徴量抽出器から特徴量を得る部分(すなわち図2の特徴量抽出器$SFR.FtrExt$のうち,x ←$FR.FtrExt$(Face) の部分)で,2つ目が特徴量をシェアにして統計的距離の計算を秘密計算で行う部分(すなわち図2の特徴量抽出器$SFR.FtrExt$のうち(x1, …, xn)←$SC.Share(x)$から顔認証機能$FR.FtrExt$全体)である.
実装した秘匿顔認証において,特徴量の形式ごとに関する顔画像の特徴量の抽出にかかる時間を表7に,特徴量間の統計的距離の計算の時間と精度を図3,4と表8にそれぞれ示す.以降では各結果についてそれぞれ説明する.
Table 7 Feature extraction time in face images.
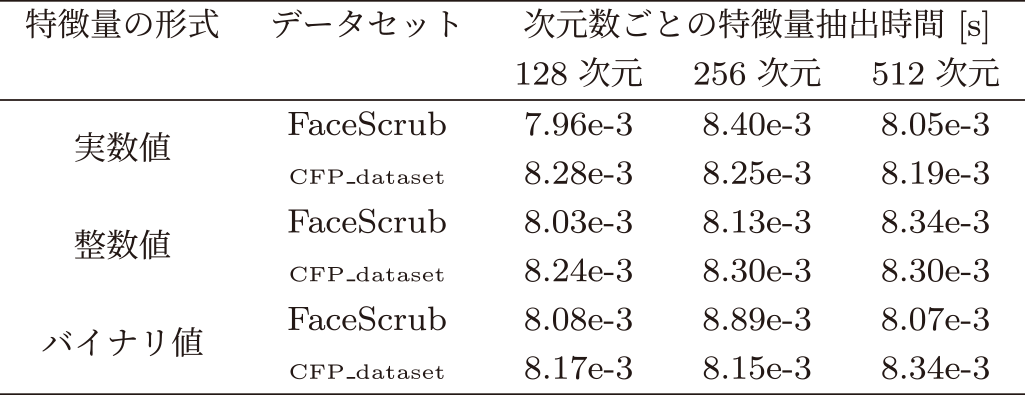
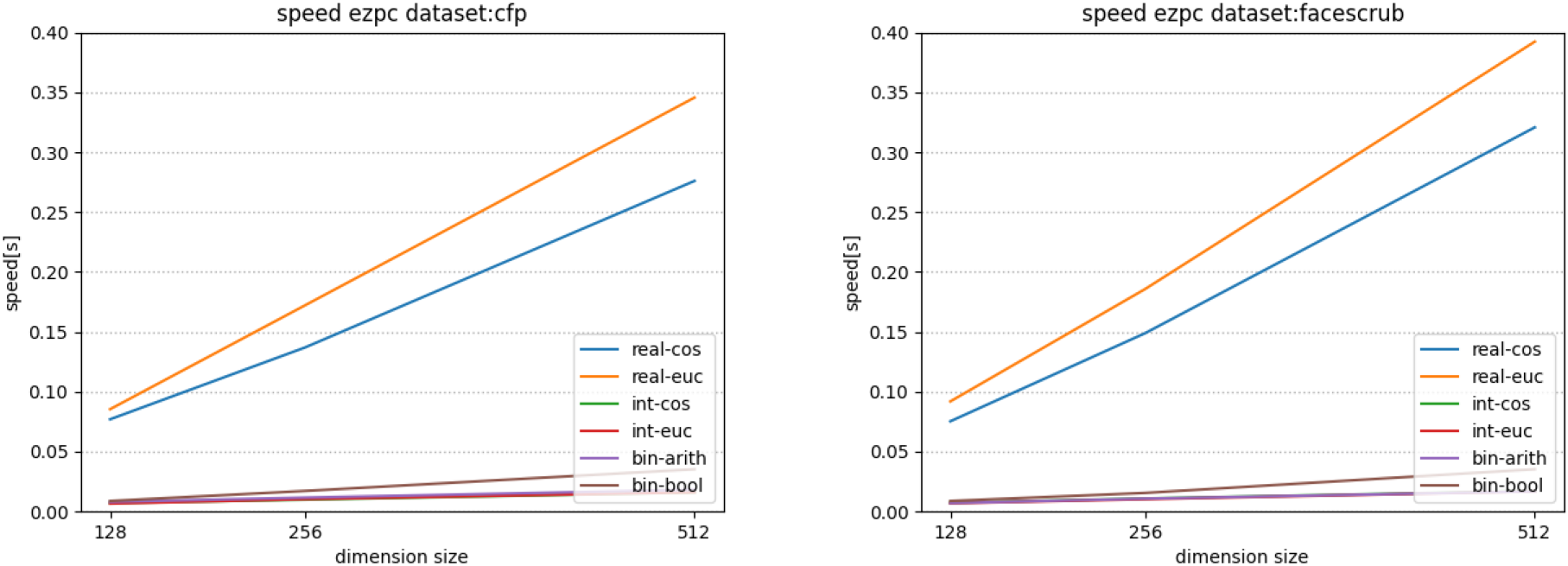
Fig. 3 EzPC: Execution time per authentication.
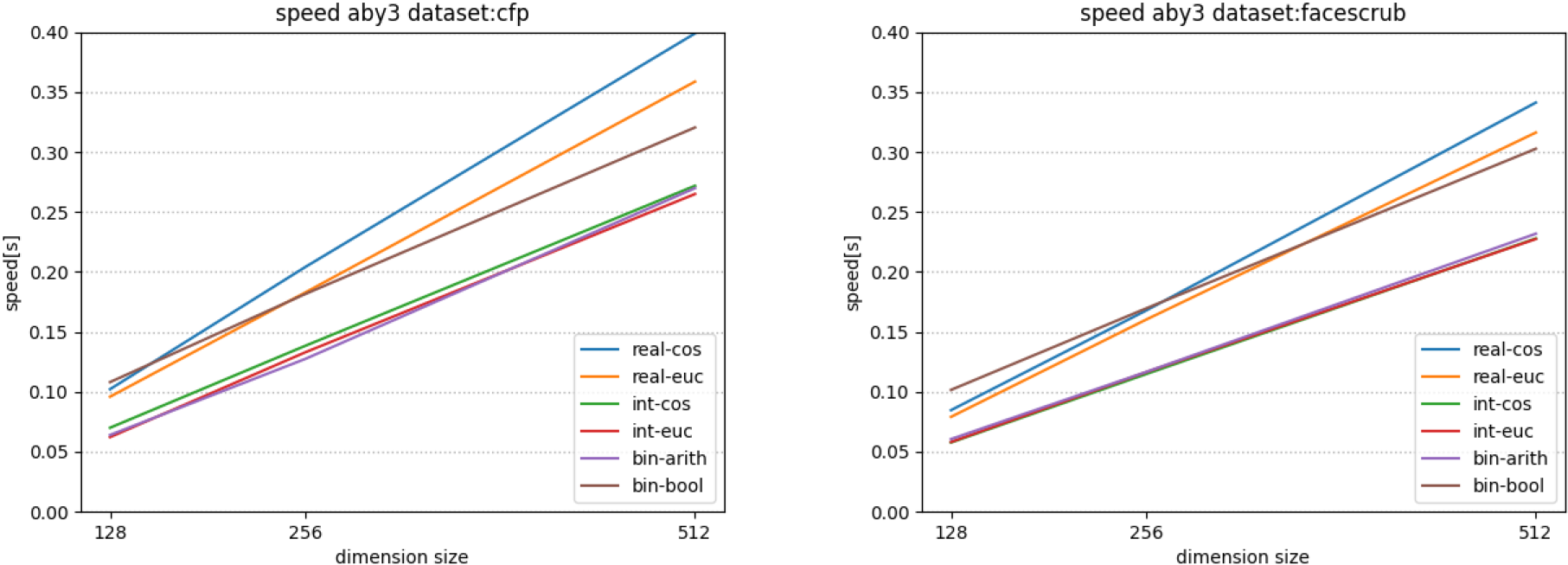
Fig. 4 ABY3: Execution time per authentication.
Table 8 Accuracy of face authentication using secure computation.

5.3.1 特徴量の形式ごとにおける顔画像の特徴量の抽出
本節では,1つ目の特徴量抽出の計算にかかる時間について述べる.特徴量抽出にかかる時間,つまり図2の特徴量抽出器$SFR.FtrExt$のうち,x ←$FR.FtrExt$(Face) の部分に関する時間を表7に示す.これらの時間は,機械学習モデルに顔画像を入力として与え,特徴量を得るまでの時間を表す.
ただし,整数値は実数値で得た特徴量を整数値へ変換する処理を含めたものである.表7に示すように各特徴量の形式と次元数によらない結果となった.実数値をベースラインとすると,整数値とバイナリ値を得る際の各変換処理による影響は十分に小さく,実験の計算機環境を考えると,これらの差は誤差程度であると考えられる.すなわち,どの特徴量の形式を用いるかは,認証における特徴量間の統計的距離の計算に従って決めることが望ましいといえる.提案する構成としてはここで得られた特徴量をシェアとしてサーバに送信し計算が行われる.
5.3.2 特徴量間の統計的距離の計算
5.3.2.1 計算時間
認証における特徴量間の統計的距離の計算時間について,図3,4に示す.これらの図は,特徴量をシェアにして統計的距離の計算を秘密計算で行う部分(すなわち図2の特徴量抽出器$SFR.FtrExt$のうち(x1, …, xn)←$SC.Share(x)$の部分と顔認証機能$SFR.FaceRcg$全体の計算時間を表す.
各図は各秘密計算ライブラリを用いて,各データセットにおける実数値,整数値,バイナリ値での計算時間を示している.図中では実数値を$real$,整数値を$int,$バイナリ値を$bin$,コサイン類似度を$cos$,ユークリッド距離を$euc$として表す.なお,バイナリ値においては,整数シェアのみを用いた場合を$arith$,バイナリシェアと整数シェアを用いた場合を$bool$として表す.
図3,4から,浮動小数点に対応しているEzPCを用いて実数値で計算した場合でも,ABY3の固定小数点の実数値と同程度の速さであることを確認できた.これらの処理は,1秒以内におさまっていることから1対1顔認証においては充分に高速であるといえる.
一方で,図3で実数値と整数値の計算時間に差がある.これはEzPCでは整数値,バイナリ値ではABY3にもとづく計算をしていることに対し,実数値では浮動小数点に対応するためにガーブル回路にもとづくアルゴリズムを用いているからだと考えられる.ABY3では,実数値を固定小数点として整数に変換したのちに整数シェアとして扱っているため整数値と実数値との計算の差がEzPCに比べると小さい.また,想定どおり,いずれの結果でも次元数の増加により計算時間が増加している.
いずれのライブラリを用いても,固定小数点である整数値を用いた際にそれぞれのライブラリで最も高速な結果となった.なかでも最も高速なのは特徴量の形式に整数値を用いた際に,cfpデータセットで次元数が128次元でユークリッド距離をEzPCを用いて計算したときで,1回の認証にかかる計算時間が6.0ミリ秒となった.同様に整数値を用いた際に,cfpデータセット,次元数128次元,EzPCでコサイン類似度を計算した場合,1回の認証にかかる計算時間は6.4ミリ秒となり大きな差がなかった.さらに,図3,4のFaceScrubデータセットの評価を見ると,実数値と整数値それぞれにおいて,コサイン類似度とユークリッド距離の計算時間に大きな変化が見受けられなかった.この理由については,実数値と整数値でのユークリッド距離とコサイン類似度の関係に依存すると考えられる.具体的には,実数値と整数値での計算において,特徴量を正規化した後のユークリッド距離を計算した場合,その結果はコサイン類似度と等しくなる.そのため,コサイン類似度とユークリッド距離の計算時間に大きな差が見受けられなかった.
次に,図3,4において,計算時間を短くするために,バイナリ値を用いたが計算時間の短縮には繋がらなかった.ハミング距離は,バイナリシェアで計算するよりも整数シェアで計算するほうが早く計算できる結果となった.つまり,バイナリ値でバイナリシェアを用いた場合,整数シェアを用いた場合よりも計算に時間を要している.この理由については,バイナリシェアを用いた場合,ハミング距離を求めるためにXORの計算の後で整数シェアに変換する必要があることが挙げられる.このシェア変換に時間がかかるため[10], [68],始めから整数シェアとして計算したほうが計算時間が短くなっている.
5.3.2.2 認証精度
秘匿顔認証の精度を表8に示す.この表の精度はABY3, EzPCいずれを用いた場合でも同じ結果となる.秘密計算時に誤差が生じるためユークリッド距離とコサイン類似度での精度が一致していない箇所も存在するが,秘密計算による誤差が小さいことが確認できる.
実数値をベースとしたときに,特徴量の違いによる精度の変化について述べる.特徴量を整数値にするモデルの精度は,平文の状態では認証精度に大きな誤差が生じないことが知られている[79], [40].本実験でも特徴量の形式が実数値と整数値である違いによる精度の差が小さいことが確認できる.また,特徴量の形式をバイナリ値にするモデルでは実数値のモデルと比べて,情報量の削減により精度が落ちている一方,ハミング距離の計算では誤差が生じることがなく,精度劣化は見受けられなかった.これらの認証精度の結果と5.3.2.1の認証にかかる計算時間より,1対1秘匿顔認証に最も適している設定は特徴量の形式が整数値,統計的距離の計算方法がコサイン類似度といえる.
次に,次元数が減少すると情報量の削減により精度が落ちる一方で,図3, 図4に示すように次元数が減少すると計算時間が短くなるというトレードオフの関係となっている.
6. 考察
本章では,5章で得た実験結果のうち,特に秘匿化した場合の計算時間と精度にそれぞれ着目し,考察を行う.
6.1 計算時間
実験結果の図3,4においてバイナリシェアを用いた場合に,整数シェアを用いた場合よりも計算時間が増加した理由について考察する.バイナリ値をバイナリシェアにして使用する場合でも,計算の過程でバイナリシェアから整数シェアに変換する必要があるため,単純な計算以上の動作が要求されている.具体的には,バイナリシェアを用いてハミング距離を計算する際,XORは早く計算することができるが総和をとるために整数シェアに変換する必要がある.また,実数値とバイナリ値それぞれをシェアにしたとき,それぞれのシェアの大きさが変わらない.つまり,64ビットの実数値を1ビットのバイナリ値にするという情報量の削減を行ったが,シェアの大きさが変わらないため,情報量の削減が計算量の削減に影響していない.計算量を削減するためには,各ライブラリで1ビットのバイナリ値に適したシェアを実装する必要がある.このような事由により,バイナリシェアを用いると整数シェアを用いたときよりも計算に時間がかかる結果になったと考えられる.また,実数値と整数値を用いた際にユークリッド距離とコサイン類似度の計算時間に大きな差がなかった理由について考察する.ユークリッド距離の計算において,通常であれば2つのベクトルの差の二乗和の平方根を計算する.しかし秘密計算において計算量を削減するために平方根は取らず,差の二乗和をユークリッド距離として扱っている.そして,コサイン類似度は,特徴量を正規化した後のユークリッド距離を計算した場合,その結果はコサイン類似度と等しくなるため,コサイン類似度にかかる計算時間は正規化処理時間とユークリッド距離計算時間の和となる.正規化処理時間はユークリッド距離計算時間に比べると小さいため,ユークリッド距離とコサイン類似度の計算時間に大きな差が生じなかったと考えられる.
6.2 精度
表8より最も高い精度が出たのは,特徴量の形式と特徴量間の統計的距離の計算方法がそれぞれ実数値・コサイン類似度の場合である.特徴量の形式と特徴量間の統計的距離の計算方法に実数値・コサイン類似度を用いるのは顔認証における一般的な設定と一致する結果となった.ただし,5.3.2.1に示したとおり,この設定は整数値の設定とも大きな変化がみられないことから,計算時間を加味すると,整数値かつコサイン類似度が秘匿顔認証においても有効といえる.
なお,バイナリ値の場合が,実数値や整数値の場合と比べてやや精度が劣るのは特徴量の形式をバイナリ値にした際に情報が落ちたことが原因だと考えられる.考えられる原因として,本稿で用いた機械学習の構成が考えられる.本稿では,機械学習としてArcFace [18],バイナリ化手法としてHashNet [72]を用いている.そのため,他の一般的な機械学習モデル[74], [80], [81]や他のバイナリ化した機械学習モデル[73], [82]で検討することで,バイナリ値と統計的距離の関係がより明らかになると考えられる.
6.3 今後の課題
本稿における妥当性への懸念事項として,今後の課題について三点述べる.1つ目は,6.2節で述べたとおり,様々な学習モデルでも同様の実験を用いることが求められる.また,特徴量の形式をバイナリ値にした際の精度について,本稿の結果は用いた機械学習の構成に依存している可能性がある.そのため,6.2節で述べたとおり機械学習の構成に応じて精度が変化していることも考えられることから,他の機械学習モデル[74], [80], [81],とくにバイナリ値にした機械学習モデル[82]を用いた検討が求められる.
2つ目は,各秘密計算のライブラリで,シェアの大きさがバイナリ値と実数値で変わらない.そのため,1ビットのバイナリ値に適したシェアの作成等,バイナリ値での計算を最適化する実装の検討が求められる.
3つ目は,より想定する問題設定に近い環境での実装実験も検討する.本稿の評価は推論処理のみ評価しているが,実際の顔認証では顔の検出や顔画像の特徴量抽出など更なる処理が求められる.このため,実際に特徴量抽出器を,携帯などのカメラ機能を持つ機器に搭載した場合の特徴量抽出に要する時間を含めた評価が求められる.これらの検討を通じて,実用化に向けてどの程度の計算機の性能が必要なのかを明らかにする.
7. 結論
本稿では秘密計算により入力となる顔画像と顔画像データベースおよび認証結果を秘匿する1対1秘匿顔認証を提案した.とくにその設計において,秘密計算に適した顔画像の特徴量の形式および特徴量間の統計的距離の計算方法を実験を通じて明らかにした.計算時間と認証精度の双方の観点から,特徴量の形式が整数値,統計的距離の計算方法としてコサイン類似度を用いることが適している.関連して得られた知見として,まず従来秘密計算には固定小数点が好ましいとされていたが,顔画像の特徴量として浮動小数点からなる実数値を用いたとしても,実用上充分に高速な構成が可能であることを確認した.浮動小数点を用いることは,従来の1対1顔認証と同じ設定である.また,特徴量を浮動小数点から固定小数点に変換することで秘密計算による精度と計算時間への影響を抑えることが既存研究で知られているが,とくに整数値への変換によりバイナリ値よりも精度が高く,かつ,高速に計算可能であることを確認した.これらの知見を通じて,1対1秘匿顔認証における効率的な設定を示すことができた.今後の課題としては他の機械学習モデル[74], [80], [81]での実装,および,バイナリ値を用いた際の各ライブラリの最適化を行うことで,より実用的な構成を実装実験を通じて明らかにすることが挙げられる.
謝辞 本研究の一部はJST CREST(JPMJCR21M5),JSTさきがけ(JPMJPR23P6),および,科研費JP23H00479, JP22H03591の支援を受けたものである.
実験用コード 本稿の実験用コードは,実験の再現性の担保および更なる発展研究の促進のために,読者の要求に応じて共有を検討している.
参考文献
- [1] Bschoff, P. and Moody, G.: Facial recognition technology (FRT): 100 countries analyzed (2021).
- [2] Murakami, T., Fujita, R., Ohki, T., Kaga, Y., Fujio, M. and Takahashi, K.: Cancelable Permutation-Based Indexing for Secure and Efficient Biometric Identification, IEEE Access, Vol.7, pp.45563–45582 (2019).
- [3] 27, I. J. S.: ISO/IEC 24745: 2011, information technology - security techniques - biometric information protection (2011).
- [4] Ma, Y., Wu, L., Gu, X., He, J. and Yang, Z.: A Secure Face-Verification Scheme Based on Homomorphic Encryption and Deep Neural Networks, IEEE Access, Vol.5, pp.16532–16538 (2017).
- [5] Dowlin, N., Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K., Naehrig, M. and Wernsing, J.: CryptoNets: Applying Neural Networks to Encrypted Data with High Throughput and Accuracy, Proc. of ICML 2016, pp.201–210 (2016).
- [6] Byali, M., Chaudhari, H., Patra, A. and Suresh, A.: FLASH: Fast and Robust Framework for Privacypreserving Machine Learning, Proceedings on Privacy Enhancing Technologies, Vol.2, pp.459–480 (2020).
- [7] Chaudhari, H., Rachuri, R. and Suresh, A.: Trident: Efficient 4PC Framework for Privacy Preserving Machine Learning, Proc. of NDSS 2020, The Internet Society (2020).
- [8] Dalskov, A. P. K., Escudero, D. and Keller, M.: Secure Evaluation of Quantized Neural Networks, CoRR, Vol.abs/1910.12435 (2019).
- [9] Jiang, X., Kim, M., Lauter, K. E. and Song, Y.: Secure Outsourced Matrix Computation and Application to Neural Networks, Proc. of CCS 2018, ACM, pp.1209–1222 (2018).
- [10] Kitai, H., Cruz, J. P., Yanai, N., Nishida, N., Oba, T., Unagami, Y., Teruya, T., Attrapadung, N., Matsuda, T. and Hanaoka, G.: MOBIUS: Model-Oblivious Binarized Neural Networks, IEEE Access, Vol.7, pp.139021–139034 (2019).
- [11] Mohassel, P. and Rindal, P.: ABY3: A Mixed Protocol Framework for Machine Learning, Proc. of CCS 2018, ACM, pp.35–52 (2018).
- [12] Mohassel, P. and Zhang, Y.: SecureML: A System for Scalable Privacy-Preserving Machine Learning, Proc. of IEEE S&P 2017, IEEE, pp.19–38 (2017).
- [13] Patra, A. and Suresh, A.: BLAZE: Blazing Fast Privacy-Preserving Machine Learning, Proc. of NDSS 2020, The Internet Society (2020).
- [14] Sav, S., Pyrgelis, A., Troncoso-Pastoriza, J. R., Froelicher, D., Bossuat, J., Sousa, J. S. and Hubaux, J.: POSEIDON: Privacy-Preserving Federated Neural Network Learning, Proc. of NDSS 2021, Internet Society (2021).
- [15] Wagh, S., Gupta, D. and Chandran, N.: SecureNN: 3-Party Secure Computation for Neural Network Training, Proceedings on Privacy Enhancing Technologies, Vol.2019, No.3, pp.26 – 49 (2019).
- [16] Kitai, H., Yanai, N., Iwahana, K., Tatsumi, M. and Cruz, J. P.: MOTUS: How Quantized Parameters Improve Protection of Model and Its Inference Input, Proc. of SECITC 2022, LNCS, Vol.13809, Springer, pp.184–202 (2022).
- [17] Iwahana, K., Yanai, N., Cruz, J. P. and Fujiwara, T.: SPGC: Integration of Secure Multiparty Computation and Differential Privacy for Gradient Computation on Collaborative Learning, Journal of Information Processing, Vol.30, pp.209–225 (2022).
- [18] Deng, J., Guo, J., Xue, N. and Zafeiriou, S.: ArcFace: Additive Angular Margin Loss for Deep Face Recognition, Proc. of CVPR 2019, IEEE, pp.4690–4699 (2019).
- [19] Kumar, N., Rathee, M., Chandran, N., Gupta, D., Rastogi, A. and Sharma, R.: CrypTFlow: Secure Tensor-Flow Inference, Proc. of IEEE S&P 2020, IEEE, pp.1646–1663 (2020).
- [20] Chandran, N., Gupta, D., Rastogi, A., Sharma, R. and Tripathi, S.: EzPC: Programmable and Efficient Secure Two-Party Computation for Machine Learning, Proc. of IEEE EuroS&P 2019, IEEE, pp.496–511 (2019).
- [21] Meden, B., Rot, P., Terh¨orst, P., Damer, N., Kuijper, A., Scheirer, W. J., Ross, A., Peer, P. and ˇStruc, V.: Privacy-Enhancing Face Biometrics: A Comprehensive Survey, IEEE Transactions on Information Forensics and Security, Vol.16, pp.4147–4183 (2021).
- [22] Das, A., Degeling, M., Wang, X., Wang, J., Sadeh, N. and Satyanarayanan, M.: Assisting Users in a World Full of Cameras: A Privacy-Aware Infrastructure for Computer Vision Applications, Proc. of CVPRW 2017, IEEE, pp.1387–1396 (2017).
- [23] Zhang, Y., Lu, Y., Nagahara, H. and Taniguchi, R.-i.: Anonymous Camera for Privacy Protection, Proc. of ICPR 2014, IEEE, pp.4170–4175 (2014).
- [24] Yuan, L. and Ebrahimi, T.: Image privacy protection with secure JPEG transmorphing, IET Signal Process., Vol.11, No.9, pp.1031–1038 (2017).
- [25] Erdélyi, Á., Barat, T., Valet, P., Winkler, T. and Rinner, B.: Adaptive cartooning for privacy protection in camera networks, Proc. of AVSS 2014, IEEE, pp.44–49 (2014).
- [26] Fradi, H., Eiselein, V., Keller, I., Dugelay, J.-L. and Sikora, T.: Crowd context-dependent privacy protection filters, Proc. of DSP 2013, IEEE, pp.1–6 (2013).
- [27] Winkler, T. and Rinner, B.: TrustCAM: Security and Privacy-Protection for an Embedded Smart Camera Based on Trusted Computing, Proc. of AVSS 2010, IEEE, pp.593–600 (2010).
- [28] Ruchaud, N. and Dugelay, J.-L.: ASePPI: Robust Privacy Protection Against De-Anonymization Attacks, Proc. of CVPRW 2017, IEEE, pp.1352–1359 (2017).
- [29] Kobayashi, K., Iwamura, K., Kaneda, K. and Echizen, I.: Surveillance Camera System to Achieve Privacy Protection and Crime Prevention, Proc. of IIH-MSP 2014, IEEE, pp.463–466 (2014).
- [30] Korshunov, P. and Ebrahimi, T.: Using face morphing to protect privacy, Proc. of AVSS 2013, IEEE, pp.208–213 (2013).
- [31] Chamikara, M. A. P., Bertok, P., Khalil, I., Liu, D. and Camtepe, S.: Privacy Preserving Face Recognition Utilizing Differential Privacy, Computers&Security, Vol.97, p.101951 (2020).
- [32] Fan, L.: Image Pixelization with Differential Privacy, Proc. of DBSec 2018, LNCS, Vol.10980, Springer, pp.148–162 (2018).
- [33] Fan, L.: Practical Image Obfuscation with Provable Privacy, Proc. of ICME 2019, IEEE, pp.784–789 (2019).
- [34] Boddeti, V. N.: Secure Face Matching Using Fully Homomorphic Encryption, Proc. of BTAS 2018, pp.1–10 (2018).
- [35] Osadchy, M., Pinkas, B., Jarrous, A. and Moskovich, B.: SCiFI - A System for Secure Face Identification, Proc. of IEEE S&P 2010, IEEE, pp.239–254 (2010).
- [36] Erkin, Z., Franz, M., Guajardo, J., Katzenbeisser, S., Lagendijk, I. and Toft, T.: Privacy-Preserving Face Recognition, Proc. of PETS 2009, LNCS, Vol.5672, Springer, pp.235–253 (2009).
- [37] Yao, A. C.: How to Generate and Exchange Secrets (Extended Abstract), Proc. of IEEE FOCS 1986, IEEE, pp.162–167 (1986).
- [38] Sadeghi, A.-R., Schneider, T. and Wehrenberg, I.: Efficient Privacy-Preserving Face Recognition, Proc. of ICISC 2009, LNSC, Vol.5984, Springer, pp.229–244 (2010).
- [39] Blanton, M. and Gasti, P.: Secure and Efficient Protocols for Iris and Fingerprint Identification, Proc. of ESORICS 2011, LNCS, Vol.6879, Springer, pp.190–209 (2011).
- [40] Tamiya, H., Isshiki, T., Mori, K., Obana, S. and Ohki, T.: Improved Post-quantum-secure Face Template Protection System Based on Packed Homomorphic Encryption, Proc. of BIOSIG 2021, LNI, Vol.P-315, Gesellschaft f¨ur Informatik e.V., pp.91–100 (2021).
- [41] Drozdowski, P., Buchmann, N., Rathgeb, C., Margraf, M. and Busch, C.: On the Application of Homomorphic Encryption to Face Identification, Proc. of BIOSIG 2019, IEEE, pp.1–5 (2019).
- [42] 菊池 亮,五十嵐大:秘密計算の発展,電子情報通信学会基礎・境界ソサイエティFundamentals Review, Vol.12, No.1, pp.12–20 (2018).
- [43] Kaur, H. and Khanna, P.: Privacy Preserving Remote Multi-Server Biometric Authentication Using Cancelable Biometrics and Secret Sharing, Future Generation Computer Systems, Vol.102, No.C, pp.30–41 (2020).
- [44] Gomez-Barrero, M., Maiorana, E., Galbally, J., Campisi, P. and Fierrez, J.: Multi-biometric template protection based on Homomorphic Encryption, Pattern Recognition, Vol.67, pp.149–163 (2017).
- [45] Rathgeb, C. and Uhl, A.: A Survey on Biometric Cryptosystems and Cancelable Biometrics, Eurasip Journal on Information Security, Vol.2011, No.1, pp.1–25 (2011).
- [46] Gentry, C.: Fully homomorphic encryption using ideal lattices, In Proc. of STOC 2009, ACM, pp.169–178 (2009).
- [47] Barni, M., Bianchi, T., Catalano, D., Di Raimondo, M., Labati, R. D., Failla, P., Fiore, D., Lazzeretti, R., Piuri, V., Piva, A. and Scotti, F.: A privacy-compliant fingerprint recognition system based on homomorphic encryption and Fingercode templates, Proc. of BTAS 2010, pp.1–7 (2010).
- [48] Bianchi, T., Turchi, S., Piva, A., Donida Labati, R., Piuri, V. and Scotti, F.: Implementing FingerCode-based identity matching in the encrypted domain, Proc. of BIMS 2010, IEEE, pp.15–21 (2010).
- [49] Barni, M., Orlandi, C. and Piva, A.: A privacypreserving protocol for neural-network-based computation, Proc. of MM&Sec 2006, ACM, pp.146–151 (2006).
- [50] Bost, R., Popa, R. A., Tu, S. and Goldwasser, S.: Machine Learning Classification over Encrypted Data, Proc. of NDSS 2015, Internet Society (2015).
- [51] Dathathri, R., Saarikivi, O., Chen, H., Laine, K., Lauter, K., Maleki, S., Musuvathi, M. and Mytkowicz, T.: CHET: An Optimizing Compiler for Fully-Homomorphic Neural-Network Inferencing, Proc. of PLDI 2019, ACM, pp.142–156 (2019).
- [52] Juvekar, C., Vaikuntanathan, V. and Chandrakasan, A.: GAZELLE: A Low Latency Framework for Secure Neural Network Inference, Proc. of USENIX Security 2018, USENIX Association, pp.1651–1668 (2018).
- [53] Liu, J., Juuti, M., Lu, Y. and Asokan, N.: Oblivious Neural Network Predictions via MiniONN transformations, Proc. of CCS 2017, ACM, pp.619–631 (2017).
- [54] Lou, Q., Bian, S. and Jiang, L.: AutoPrivacy: Automated Layer-wise Parameter Selection for Secure Neural Network Inference, Proc. of NeurIPS 2020, Vol.33, Curran Associates, Inc., pp.8638–8647 (2020).
- [55] Orlandi, C., Piva, A. and Barni, M.: Oblivious Neural Network Computing via Homomorphic Encryption, EURASIP Journal on Information Security, Vol.2007, No.1 (2007).
- [56] Riazi, M. S., Samragh, M., Chen, H., Laine, K., Lauter, K. E. and Koushanfar, F.: XONN: XNOR-based Oblivious Deep Neural Network Inference, Proc. of USENIX Security 2019, USENIX Association, pp.1501–1518 (2019).
- [57] Riazi, M. S., Weinert, C., Tkachenko, O., Songhori, E. M., Schneider, T. and Koushanfar, F.: Chameleon: A Hybrid Secure Computation Framework for Machine Learning Applications, Proc. of ASIACCS 2018, ACM, pp.707–721 (2018).
- [58] Rouhani, B. D., Riazi, M. S. and Koushanfar, F.: Deepsecure: scalable provably-secure deep learning, Proc. of DAC 2018, ACM, pp.2: 1–2: 6 (2018).
- [59] Samragh, M., Hussain, S., Zhang, X., Huang, K. and Koushanfar, F.: On the Application of Binary Neural Networks in Oblivious Inference, Proc. of CVPRW 2021, IEEE, pp.4630–4639 (2021).
- [60] Zhang, Q., Xin, C. and Wu, H.: GALA: Greedy ComputAtion for Linear Algebra in Privacy-Preserved Neural Networks, Proc. of NDSS 2021, Internet Society (2021).
- [61] Fredrikson, M., Lantz, E., Jha, S., Lin, S., Page, D. and Ristenpart, T.: Privacy in Pharmacogenetics: An End-to-End Case Study of Personalized Warfarin Dosing, Proc. of USENIX Security 2014, USENIX Association, pp.17–32 (2014).
- [62] Tramèr, F., Zhang, F., Juels, A., Reiter, M. K. and Ristenpart, T.: Stealing Machine Learning Models via Prediction APIs, Proc. of USENIX Security 2016, USENIX Association, pp.601–618 (2016).
- [63] Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I., Talwar, K. and Zhang, L.: Deep learning with differential privacy, Proc. of SIGSAC 2016, ACM, pp.308–318 (2016).
- [64] Yeom, S., Giacomelli, I., Fredrikson, M. and Jha, S.: Privacy Risk in Machine Learning: Analyzing the Connection to Overfitting, Proc. of CSF 2018, IEEE, pp.268–282 (2018).
- [65] Szyller, S., Atli, B. G., Marchal, S. and Asokan, N.: DAWN: Dynamic Adversarial Watermarking of Neural Networks, Proc. of MM 2021, ACM, pp.4417–4425 (2021).
- [66] Goldreich, O., Micali, S. and Wigderson, A.: How to Play ANY Mental Game, Proc. of STOC 1987, ACM, pp.218–229 (1987).
- [67] Ben-Or, M., Goldwasser, S. and Wigderson, A.: Completeness Theorems for Non-Cryptographic Fault-Tolerant Distributed Computation, Proc. of STOC 1988, ACM, pp.1–10 (1988).
- [68] Demmler, D., Schneider, T. and Zohner, M.: ABY - A Framework for Efficient Mixed-Protocol Secure Two-Party Computation, Proc. of NDSS 2015, The Internet Society (2015).
- [69] Knott, B., Venkataraman, S., Hannun, A. Y., Sengupta, S., Ibrahim, M. and van der Maaten, L.: CrypTen: Secure Multi-Party Computation Meets Machine Learning, Proc. of NeurIPS 2021, Vol.34, Curran Associates, Inc., pp.4961–4973 (2021).
- [70] Patra, A., Schneider, T., Suresh, A. and Yalame, H.: ABY2.0: Improved Mixed-Protocol Secure Two-Party Computation, Proc. of USENIX Security 2021, USENIX Association, pp.2165–2182 (2021).
- [71] Bourse, F., Minelli, M., Minihold, M. and Paillier, P.: Fast Homomorphic Evaluation of Deep Discretized Neural Networks, Proc. of CRYPTO 2018, LNCS, Vol.10993, Springer, pp.483–512 (2018).
- [72] Cao, Z., Long, M., Wang, J. and Yu, P. S.: HashNet: Deep Learning to Hash by Continuation, Proc. of ICCV 2017, IEEE, pp.5609–5618 (2017).
- [73] Courbariaux, M., Hubara, I., Soudry, D., El-Yaniv, R. and Bengio, Y.: Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1, CoRR, Vol.abs/1602.02830 (2016).
- [74] Wang, H., Wang, Y., Zhou, Z., Ji, X., Gong, D., Zhou, J., Li, Z. and Liu, W.: CosFace: Large Margin Cosine Loss for Deep Face Recognition, Proc. of CVPR 2018, IEEE, pp.5265–5274 (2018).
- [75] Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J. and Chintala, S.: PyTorch: An Imperative Style, High-Performance Deep Learning Library, Proc. of NeurIPS 2019, Vol.32, Curran Associates, Inc., pp.8024–8035 (2019).
- [76] Cao, Q., Shen, L., Xie, W., Parkhi, O. M. and Zisserman, A.: VGGFace2: A Dataset for Recognising Faces across Pose and Age, Proc. of IEEE FG 2018, IEEE, pp.67–74 (2018).
- [77] Sengupta, S., Chen, J., Castillo, C. D., Patel, V. M., Chellappa, R. and Jacobs, D. W.: Frontal to profile face verification in the wild, Proc. of WACV 2016, IEEE, pp.1–9 (2016).
- [78] Ng, H.-W. and Winkler, S.: A data-driven approach to cleaning large face datasets, Proc. of IEEE ICIP 2014, IEEE, pp.343–347 (2014).
- [79] Kitai, H., Cruz, J. P., Yanai, N., Nishida, N., Oba, T., Unagami, Y., Teruya, T., Attrapadung, N., Matsuda, T. and Hanaoka, G.: MOBIUS: Model-Oblivious Binarized Neural Networks, IEEE Access, Vol.7, pp.139021–139034 (2019).
- [80] Duan, Y., Lu, J. and Zhou, J.: UniformFace: Learning Deep Equidistributed Representation for Face Recognition, Proc. of CVPR 2019, pp.3415–3424 (2019).
- [81] Meng, Q., Zhao, S., Huang, Z. and Zhou, F.: MagFace: A Universal Representation for Face Recognition and Quality Assessment, Proc. of CVPR 2021, IEEE, pp.14220–14229 (2021).
- [82] Kang, R., Cao, Y., Long, M., Wang, J. and Yu, P. S.: Maximum-Margin Hamming Hashing, Proc. of ICCV 2019, IEEE, pp.8251–8260 (2019).
脚注
- *1 一般の顔認証アルゴリズムではこれらの他に顔認識機能が求められるが,本稿の提案アルゴリズムでこれを用いることはないため説明は割愛する.
- *2 さもなくばシェアから元の特徴量を求めることが可能になる.
- *3 https://github.com/deepinsight/insightface/tree/master/recognition/arcface_torch.
- *4 https://github.com/ladnir/aby3.
- *5 https://github.com/mpc-msri/EzPC.
2024年大阪大学大学院情報科学研究科博士前期課程修了.修士(情報科学).在学中,機械学習と暗号理論の研究に従事.

2021年京都大学大学院情報学研究科博士後期課程修了.2023年大阪大学着任,現在に至る.大阪大学大学院情報科学研究科助教.公開鍵暗号系を中心とする暗号理論の研究に従事.博士(情報学).

2009年一関高専・生産工学専攻修了.2011年筑波大・大学院システム情報工学研究科博士前期課程了.2014年同大学院博士後期課程了.2014年大阪大・大学院情報科学研究科・助教,2021年同大学院・准教授,現在に至る.博士(工学).電子情報通信学会,情報処理学会各会員.

2000年大阪大学基礎工学部情報科学科卒業.2002年同大学大学院基礎工学研究科博士前期課程修了.2005年同博士後期課程修了.博士(情報科学).2005年大阪大学サイバーメディアセンター特任助手.2007年同特任助教.2008年同大学大学院情報科学研究科特任助教.2008年10月奈良工業高等専門学校情報工学科助教.2011年同講師.2013年同准教授.2024年同教授.暗号プロトコルとサイバーセキュリティの研究に従事.電子情報通信学会,電気学会,IEEE,IACR各会員.
採録日 2024年5月20日