A study on learning algorithms of value and policy functions in Hex

 ボードゲームをプレイするコンピュータプレイヤの開発に関する研究は，ゲーム情報学と呼ばれる研究分野に分類される研究です．ゲーム情報学では，様々なゲームを対象に探索手法，データベース，機械学習，心理学など幅広い分野にまたがって研究が行われています．その中でも，人間を超えるコンピュータプレイヤを開発することはグランドチャレンジの1つとして捉えられ，強いコンピュータプレイヤを開発するための研究が数多く行われています．優れたコンピュータプレイヤを開発するためには，現在の局面から起こり得る全局面という膨大な探索空間から，コンピュータプレイヤにとって最良な手を効率的に探索する手法が必要となります．こういった手法の開発過程で得られる探索アルゴリズムや機械学習アルゴリズムは，人工知能の分野等への応用が期待されています．

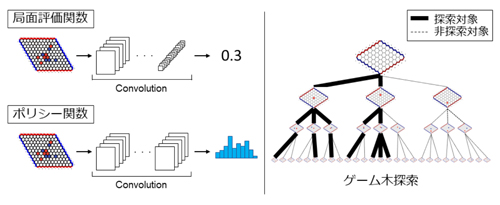
 本研究では，Hexと呼ばれるボードゲームを対象に，より強いコンピュータプレイヤを開発するための機械学習アルゴリズムの提案を行いました．Hexは数学者のPiet HeinやJohn Nashらに開発された二人用ボードゲームであり，チェスや将棋や囲碁と同様に二人零和有限確定完全情報ゲームに分類されるボードゲームです．二人用ボードゲームをプレイするコンピュータプレイヤを開発するためには，現在の局面の形勢を定量化する局面評価関数と候補手の有望性を定量化するポリシー関数が必要となります．そして，高精度な2つの評価関数を使用することで，より良い手を探索することが可能になり，より強いコンピュータプレイヤの開発に繋がります．先行研究では，高精度な評価関数を作成するために，人間のプロ棋士の手を打つように評価関数を学習させる機械学習アルゴリズムや，自己対戦を通した強化学習アルゴリズムなどが提案されてきました．特に，自己対戦を利用した強化学習アルゴリズムは人間のプロ棋士を超えるコンピュータプレイヤの開発に繋がると期待され，近年では強化学習アルゴリズムによって作成されたコンピュータプレイヤが囲碁のトッププロ棋士を破っています．一方で，人間のトッププロ棋士に勝つレベルのコンピュータプレイヤを開発するためには，非常に大きな計算リソースが必要となることが知られています．そこで，私は従来手法に比べ低コストで高精度な評価関数を作成し得る手法であり，自己対戦を通して局面評価関数とポリシー関数を作成する強化学習アルゴリズムを提案しました．既存のコンピュータプレイヤや，他の学習アルゴリズムとの比較を通して，提案手法によって高精度な局面評価関数とポリシー関数が作成可能であることを示しました．