A Novel Catadioptric Ray-Pixel Camera Model and its Application to 3D Reconstruction

 コンピュータにおける視覚情報処理を研究対象とするコンピュータビジョン分野において，撮影画像から対象物体の３次元形状を復元することは重要な課題である．人が視覚によって色・動き・位置・形といった外界の多くの情報を得ているように，コンピュータビジョンはそのような視覚情報を撮影画像から得ることを考える．中でも３次元形状は外界に働きかけるための主要な情報の1つであり，その獲得技術はこれまで文化財等の記録保存や，自分の周囲の地図作成，手術ナビゲーション，製品検査をはじめとしてさまざまなものに応用されている．

 そして，コンピュータにとっての目となるカメラ自体も，レンズや鏡を利用して拡大率や視点を変化させることでさまざまな用途に応用されている．たとえば，レンズによる屈折は顕微鏡や望遠鏡のように拡大率を変化させることができ，鏡による反射は車のバックミラーのように視点を変化させることができる．このように反射および屈折を利用した撮像システムは反射屈折撮像系と呼ばれ，曲面鏡を使った全方位撮影など，人がそのまま見るためではなくコンピュータの計算処理を前提とした撮像システムも存在する．

 しかしながら，このような反射屈折撮像系に対しては，従来の3次元形状復元の技術をそのまま適用することができない．なぜなら従来の3次元位置の計算手法のほとんどにおいて，対象物体からカメラへと向かう光の方向が屈折や反射で変化することを想定していなかったからである．

 本研究は，屈折や反射を考慮した3次元位置の計算手法を対象とした研究分野に位置づけられる．このような分野において，3次元位置の計算の根幹となるのはカメラモデルと呼ばれるものであり，これは3次元シーンと2次元画像のそれぞれの位置を結びつける物理的な光の投影経路の計算モデルである．反射屈折撮像系のためのカメラモデルとしては大きく分けて2種類のものがすでに提案されている．1つ目は屈折層の形や鏡の位置を推定した上で，画像上の位置に対応する光路を解析的に計算する方法である．2つ目はどのように反射・屈折したかは計算せずに，あらかじめ画像上の位置に対応する光路を記憶しておく方法である．ただし，これらの方法はどちらの場合においても，画像上の位置から対応するシーンの光線は直ちに得られるが，3次元シーンのある位置から対応する光線を得るためには高い計算コストが要求されることが知られている．

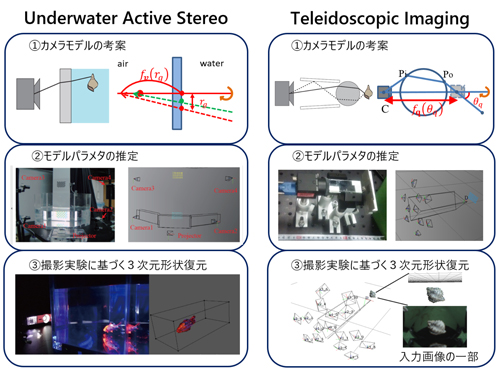
 これに対し本研究のアイディアは，シーンからカメラ画像上のすべての位置へと投影される光線全体を見たときに，その光線同士の大小関係や向きの分布に着目することによって，3次元シーンのある位置からの光線の計算を効率的に行うことである．さらにその具体的な応用として，屈折を考慮した水中物体の3次元形状復元（左図）および，鏡とレンズの配置の工夫による微小な物体の3次元形状復元（右図）をそれぞれ実環境での撮影実験により行い，復元精度および計算コストの評価によって提案手法の有効性を示した．