モンテカルロ木探索の改善に関する研究

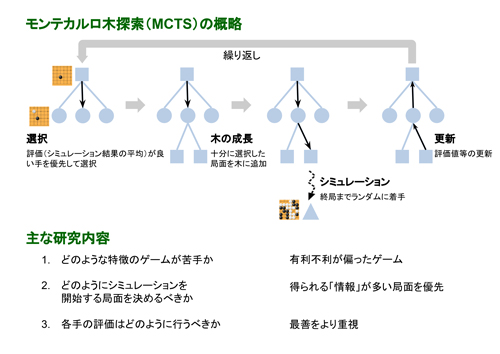
 モンテカルロ木探索（MCTS）は，木探索アルゴリズムの一種であり，シミュレーションを繰り返し，その平均的な結果が良い候補手を優先的に探索するアルゴリズムである．MCTSは汎用なアルゴリズムであり，囲碁やHexといったさまざまなゲームで有効性が確認されてきた．特に囲碁では，初めてプロ棋士に勝ったプログラムAlphaGoでの探索に採用され，その勝利に貢献した．

 しかし，MCTS は常に優れた性能を発揮できるわけではなく，比較的苦手なゲームがあることが知られている．また，代表的なMCTSではシミュレーションを開始する節点を選ぶことを多腕バンディット問題（MAB）とみなして，MABのアルゴリズムを用いているが，MABと木探索では異なる点があり，MABの性質は成り立たない．本研究では，MCTSについて，ゲームの種類とそこでの性能，妥当な理論的な仮定といった観点から多角的に議論し，既存手法の問題点を指摘し，その改善策を提示した．より具体的には，3点に着目して研究を行った．

 第1点目は，ゲームとの相性である．MCTSには比較的苦手なゲームがあると知られている．本研究では，苦手なゲームの特徴の一つとして，新たに「最善手を選び損ねた場合の不利益の偏り」という特徴に着目し，分析した．この特徴は，囲碁の中でも，MCTSが比較的苦手とされる攻め合いの局面の特徴と共通している．加えて，従来通りMABとみなした場合での理論的な分析に基づき，不利益の偏りを動的に調整する改善策を提案した．

 第2点目は，探索資源の割り振りである．本来，探索の目的は最善手を判別することであり，これはMABでの単純リグレット（最終的な選択による損失）の最小化に相当する．しかしながら，探索において，MABのアルゴリズムを使い，単純リグレットを直接最小化することは難しいため，累積リグレット（探索中の選択による累積損失）の最小化のための手法がMCTSに応用されてきた．本研究では，探索での直接的な単純リグレットの最小化を目指し，分布を使ったMCTSを提案した．提案手法は，扱う分布を勝敗の主観確率の分布と仮定すると，最善手の判別のために，探索資源の割り振りが効果的になされると期待できる手法である．

 第3点目は，評価の仕方である．最善手の判別のためには，最善を尽くした場合の評価が重要である．しかしながら，一般的なMCTSでは，シミュレーション結果の平均的な良さによって，各候補手を評価している．平均による評価では，悪手の影響を少なからず受ける．本研究では，部分的に最善を尽くした場合の勝ち負けが明らかになった場合や，一部の手がはっきりと悪い場合で，より最善を重視する評価方法を提案した．

 

（2018年5月31日受付）