(邦訳:決定グラフに基づく順列集合処理に関する研究)
| 井上 祐馬 グーグル合同会社 ソフトウェアエンジニア |
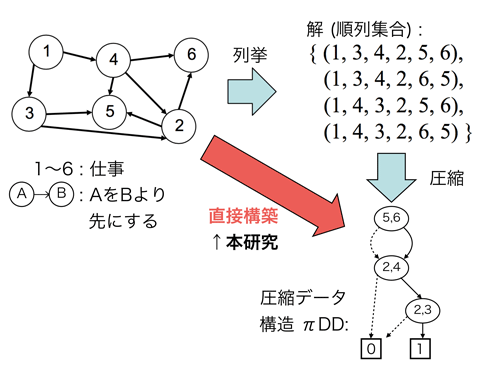
[背景]ランキングなど,条件を満たす順序の全列挙
[問題]解となる順序の数の膨大さ
[貢献]全解を圧縮表現するデータ構造,構築法の提案
[問題]解となる順序の数の膨大さ
[貢献]全解を圧縮表現するデータ構造,構築法の提案
日常生活の中でよく,人はモノに順序を付けることが必要になる.たとえば,いくつかの仕事を順に処理したり, Web検索の結果に順位を付けて表示したり,行きたい名所を順々に巡ったり,などは適切なモノの順序を決めたい場面の例である.数学の用語では,このような順序付けのことを順列と呼ぶ.数学的には,順列は集合上の全単射関数として定義されるため,ほかにも離散関数やマッチングなどを表現する場面でも現れる.
答えを順列で表せるような種々の問題に対し,“よい”順列を1つ見つけてくるような手法は,盛んに研究されてきた.たとえば,巡回セールスマン問題は“最短”で移動できるような都市の訪問順列を求める問題であり,単一機械スケジューリング問題は“最小”ペナルティとなる仕事の処理順列を求める問題である.一方で,条件を満たす順列の列挙を行うことにより,1つの順列を見つける問題を包含した,このような問題に対してより幅広い応用が期待できる.すべての解の中から最適な順列を1つとってくることもできるし,条件を満たす解の個数を数える,ランダムサンプリングを行う,追加の条件で絞り込んだものをさらに取り出す,といったことも可能となる.さまざまな条件に対し,その条件を満たす順列を列挙する研究も数多く行われてきた.これらは列挙する解の個数に依存した計算時間を要するが,解になり得る順列の個数は階乗のオーダで多くなるため,それほど大きくないモノの順列を列挙することも現実的ではなくなってしまうという問題があった.
この組合せ爆発を回避するためのアイディアとして,保存・索引化に圧縮データ構造を利用することが考えられる.本研究では,湊によって2011年に提案された,順列決定グラフ(πDD)と呼ばれるデータ構造に着目する.このデータ構造は順列の集合を圧縮して省スペースで表現できるのみならず,順列集合間の二項演算をサポートしている.さらに,保存している順列に対する書き換え操作や条件絞り込み操作などが圧縮サイズにのみ依存した時間で行える.すなわち,順列集合がπDDとしてコンパクトに圧縮されていれば,πDD上での操作も高速に行えることが期待できる.
本研究の貢献は以下に要約される.
(1)種々の順列問題に対するπDD構築アルゴリズムの提案
本研究では,さまざまな順列問題に対しπDD構築アルゴリズムを与えた.具体的には,
答えを順列で表せるような種々の問題に対し,“よい”順列を1つ見つけてくるような手法は,盛んに研究されてきた.たとえば,巡回セールスマン問題は“最短”で移動できるような都市の訪問順列を求める問題であり,単一機械スケジューリング問題は“最小”ペナルティとなる仕事の処理順列を求める問題である.一方で,条件を満たす順列の列挙を行うことにより,1つの順列を見つける問題を包含した,このような問題に対してより幅広い応用が期待できる.すべての解の中から最適な順列を1つとってくることもできるし,条件を満たす解の個数を数える,ランダムサンプリングを行う,追加の条件で絞り込んだものをさらに取り出す,といったことも可能となる.さまざまな条件に対し,その条件を満たす順列を列挙する研究も数多く行われてきた.これらは列挙する解の個数に依存した計算時間を要するが,解になり得る順列の個数は階乗のオーダで多くなるため,それほど大きくないモノの順列を列挙することも現実的ではなくなってしまうという問題があった.
この組合せ爆発を回避するためのアイディアとして,保存・索引化に圧縮データ構造を利用することが考えられる.本研究では,湊によって2011年に提案された,順列決定グラフ(πDD)と呼ばれるデータ構造に着目する.このデータ構造は順列の集合を圧縮して省スペースで表現できるのみならず,順列集合間の二項演算をサポートしている.さらに,保存している順列に対する書き換え操作や条件絞り込み操作などが圧縮サイズにのみ依存した時間で行える.すなわち,順列集合がπDDとしてコンパクトに圧縮されていれば,πDD上での操作も高速に行えることが期待できる.
本研究の貢献は以下に要約される.
(1)種々の順列問題に対するπDD構築アルゴリズムの提案
本研究では,さまざまな順列問題に対しπDD構築アルゴリズムを与えた.具体的には,
- 可逆論理回路デバッグ問題への適用
- サイクルタイプ同値類分割への応用
- オイラー路/ハミルトン路の列挙
- トポロジカル順序の列挙
- パターン回避順列の列挙
が挙げられる.これらの問題に対し,πDDを適用することで既存の手法よりも効率的な解法が得られた.具体的な問題の定義や提案手法などは本博士論文を参照されたい.
(2)πDDに変更を加えた新たなデータ構造の提案と応用
πDDの構造に変更を加えたRot-πDDというデータ構造を提案した.上述の問題のうち3つの問題において,Rot-πDDを用いることで効率が向上した.また,各々のデータ構造の効率に影響を与える順列問題の特徴について考察し,使い分けの指針を与えた.
(2)πDDに変更を加えた新たなデータ構造の提案と応用
πDDの構造に変更を加えたRot-πDDというデータ構造を提案した.上述の問題のうち3つの問題において,Rot-πDDを用いることで効率が向上した.また,各々のデータ構造の効率に影響を与える順列問題の特徴について考察し,使い分けの指針を与えた.
(2017年5月21日受付)

