Analyses of Deterministic Processes Analogous to Finite Markov Chains

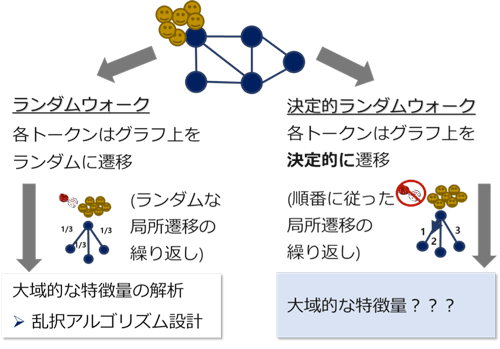
 マルコフ連鎖（ランダムウォーク）は数理モデリングや解析技法として理論計算機科学を含む多くの分野で用いられている単純かつ重要な確率過程である．たとえば，ランダムウォークはその簡素さ，局所性，構造の変化に対する耐故障性からネットワーク探索への有望なアプローチとして研究が進んでおり，またマルコフ連鎖モンテカルロ法（MCMC法）は乱択近似数え上げアルゴリズム設計の汎用手法として確立されている．これらの乱択アルゴリズムの性能はマルコフ連鎖の混交時間, 全訪問時間といった特徴量に依存しており，これまでに多くのこれらの特徴量の解析手法が開発され，確率的計算理論の基礎を為している．

 近年，ランダムウォークの代替として, 決定性ランダムウォーク（deterministic random walk）と呼ばれるマルコフ連鎖を類似する決定性過程について，ネットワークの決定的探索, 物理現象の決定的シミュレーションなど複数の文脈で研究が為されている．特に，ロータールーターモデルと呼ばれる単純ランダムウォークに対応する決定性ランダムウォークについて研究が進んでおり，超立方体，整数格子，正則グラフなどの上でその混交性, 全訪問時間の解析が与えられている．

 しかし，マルコフ連鎖に対しこれまで培われてきた研究に比べると，決定性ランダムウォークの研究はまだ黎明期であり，たとえば，単純ランダムウォークを超えた一般の遷移確率に対応する決定性過程に関する研究はほとんど為されていない．本研究では，確率的計算と決定性計算のギャップ解明を目指し，決定性ランダムウォーク解析の一般的な枠組み構築を行った．具体的には，一般の有限マルコフ連鎖に対応する決定性ランダムウォークの混交性と全訪問時間の解析を行い，本質的に大きく以下の3つの結果を与えた.

 まず，マルコフ連鎖によるトークンの期待配置と, 対応する決定性ランダムウォークにおけるトークン配置の単一頂点誤差の解析を行い, 一般の遷移確率に対応するモデルの設計と単一頂点誤差の上界を導出した．この上界は未解決であった多項式時間収束するマルコフ連鎖と対応する決定性過程との単一頂点誤差の多項式サイズ上界について肯定的な解決を与えるものである．

 次にMCMC法の脱乱択化を動機として，MCMC法に基づく乱択アルゴリズム設計において重要な指標である，総変動誤差の解析を与えた．ここでは総変動誤差に対する初の上界を与えた一方，入力の指数サイズ程度となる下界の例を与え，これはMCMC法の脱乱択化には対象の構造活用の必要性があることを示唆している．

 最後に，上記の解析が位相平均にあたるトークン分布の解析であるのに対し，時間平均に当たる訪問頻度の誤差・決定性ランダムウォークの全訪問時間の上界が与えた．この成果からエキスパンダーグラフ上の複数トークンロータールーターモデルに対し単純ランダムウォークの高速化比と同様の成果が得られ，決定性過程により確率過程と遜色ない高速化が実現できる例を示している．