(邦訳:連続ウェーブレット変換領域におけるソースフィルタ表現と位相推定によるモノラル音楽音響信号加工の研究)
| 中村 友彦 セコム(株) IS研究所 |
[背景]既存の音楽を視聴者が自由に加工して楽しむ時代の到来
[問題]音楽音響信号加工のための高精度なモノラル音源分離
[貢献]連続ウェーブレット変換領域での音源分離フレームワークの構築
本研究では,音楽音響信号を音高や楽器などの単位に分解し,分解成分を個別に加工することを可能にする音響信号分離および合成手法を提案する.これは,ユーザによる音楽制作や既存楽曲の加工支援システム,楽音を加工し聴取可能な音楽プレイヤー,計算機による自動編曲システムなどの音楽アプリケーションに応用可能である.
音響信号加工の性能は音源分離の精度に大きく依存するため,加工の前段で高精度な分離を行うことが重要である.一般に高精度な分離のためには解を適切に限定するための手がかりが必要となる.時間周波数表現(スペクトログラム)領域では調波性などの音源分離に有用な手がかりを利用できるが,適切な周波数解像度のスペクトログラムを選択するためには対象がどのような音響信号であるかを考慮することが重要である.また,そのスペクトログラム上で対象の音響信号をどのように表現できるかという点も考慮する必要がある.したがって,時間周波数表現を意識したアプローチをとるべきである.
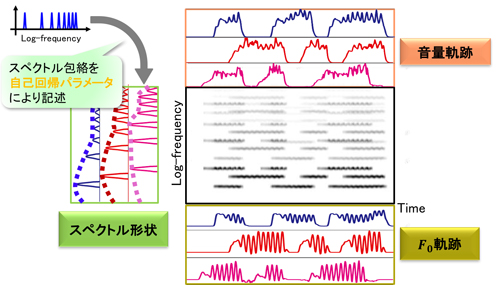
そこで,本論文では以下の3つの方針を考えこれらを同時に考慮した手法を提案した.まず第1の方針として(i)対数周波数解像度を与える連続ウェーブレット変換(continuous wavelet transform; CWT)によるスペクトログラムを利用する.これは平均律での各音高の基本周波数F0は対数尺度で均等に並ぶ性質があるからである.次に,第2の方針として(ii)楽音の生成過程モデルを活用する.ソースフィルタ理論によると楽音の生成過程は楽器の振動体と共鳴体に分離して考えることができ,楽音のスペクトルに関する仮定が見通しよく立てられるためである.第3の方針として(iii)スペクトル漏れを考慮する.実際に観測されるスペクトルが取ることを許される形状には制約があり,もしスペクトル漏れの具体的な形状や関数が分かっていれば,近接した異なる音源のF0成分や高調波成分を分離する手がかりとなるからである.これら3つの方針を同時に考慮したアプローチを実現するためには,スペクトログラム領域とソースフィルタモデルなどの時間信号領域のモデルとの対応関係を得る必要がある.しかし,CWTの基底波形は互いに直交しないためどのように対応関係を得るべきかは必ずしも知られていない.
本論文では,まず方針(i),(ii)を同時に考慮した音源分離手法,方針(i),(iii)を同時に考慮した音源分離手法をそれぞれ提案しその有効性を確認した.これら2つの手法を足がかりとして時間信号領域とCWT領域のモデルの対応関係を導出し,全方針を満たす音源分離手法を提案した.
また,分離後に加工された振幅スペクトログラムを時間信号に変換するために,振幅スペクトログラムからの高速位相推定法も提案した.スペクトログラムが信号の冗長な表現であることに着目し,時間領域信号に対応する複素スペクトログラムが満たす条件を導出した.その条件を元に位相推定問題が最適化問題として定式化し,効率的な反復アルゴリズムが導出できることを示した.著者のwebページ(http://tomohikonakamura.github.io/Tomohiko-Nakamura/demo/HTFD.html)で提案法を用いて加工した例を聴取可能である.
音響信号加工の性能は音源分離の精度に大きく依存するため,加工の前段で高精度な分離を行うことが重要である.一般に高精度な分離のためには解を適切に限定するための手がかりが必要となる.時間周波数表現(スペクトログラム)領域では調波性などの音源分離に有用な手がかりを利用できるが,適切な周波数解像度のスペクトログラムを選択するためには対象がどのような音響信号であるかを考慮することが重要である.また,そのスペクトログラム上で対象の音響信号をどのように表現できるかという点も考慮する必要がある.したがって,時間周波数表現を意識したアプローチをとるべきである.
そこで,本論文では以下の3つの方針を考えこれらを同時に考慮した手法を提案した.まず第1の方針として(i)対数周波数解像度を与える連続ウェーブレット変換(continuous wavelet transform; CWT)によるスペクトログラムを利用する.これは平均律での各音高の基本周波数F0は対数尺度で均等に並ぶ性質があるからである.次に,第2の方針として(ii)楽音の生成過程モデルを活用する.ソースフィルタ理論によると楽音の生成過程は楽器の振動体と共鳴体に分離して考えることができ,楽音のスペクトルに関する仮定が見通しよく立てられるためである.第3の方針として(iii)スペクトル漏れを考慮する.実際に観測されるスペクトルが取ることを許される形状には制約があり,もしスペクトル漏れの具体的な形状や関数が分かっていれば,近接した異なる音源のF0成分や高調波成分を分離する手がかりとなるからである.これら3つの方針を同時に考慮したアプローチを実現するためには,スペクトログラム領域とソースフィルタモデルなどの時間信号領域のモデルとの対応関係を得る必要がある.しかし,CWTの基底波形は互いに直交しないためどのように対応関係を得るべきかは必ずしも知られていない.
本論文では,まず方針(i),(ii)を同時に考慮した音源分離手法,方針(i),(iii)を同時に考慮した音源分離手法をそれぞれ提案しその有効性を確認した.これら2つの手法を足がかりとして時間信号領域とCWT領域のモデルの対応関係を導出し,全方針を満たす音源分離手法を提案した.
また,分離後に加工された振幅スペクトログラムを時間信号に変換するために,振幅スペクトログラムからの高速位相推定法も提案した.スペクトログラムが信号の冗長な表現であることに着目し,時間領域信号に対応する複素スペクトログラムが満たす条件を導出した.その条件を元に位相推定問題が最適化問題として定式化し,効率的な反復アルゴリズムが導出できることを示した.著者のwebページ(http://tomohikonakamura.github.io/Tomohiko-Nakamura/demo/HTFD.html)で提案法を用いて加工した例を聴取可能である.
(2016年6月10日受付)

