Combinatorial Optimization on Group-Labeled Graphs

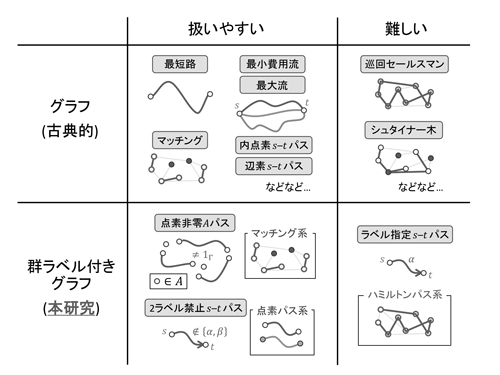
 「最短経路探索」に代表されるように，グラフにおいて指定した条件を満たす構造のうち最適なものを見つけたい，という要求は，いたるところにさまざまな形で現れる．そのような問題は「グラフにおける組合せ最適化問題」と呼ばれ，さまざまな問題に対し，その性質や解法が盛んに研究されてきた．それらの問題は，大きく分けて，入力の大きさに対してほどほどの手間（多項式時間）で解ける「扱いやすい問題」と，そうでない「難しい問題」の2種類に分類することができる．「どのような問題が扱いやすいのか」，また，「その扱いやすさは何に起因するのか」，といったことを解明することは，組合せ最適化の分野における1つの中心的なテーマである．

 本研究では，群という良い代数構造を取り入れた，ある種の一般化されたグラフにおける組合せ最適化問題に対し，そのような「扱いやすさ」の解明を目指している．今回扱った問題は以下の2つである．

（1）点素非零Aパスの詰め込み
 Mader（1978）は，グラフにおける最大マッチングとパス詰め込みという，一見大きく異なる2つの古典的な組合せ最適化問題を，「内点素Aパス詰め込み」として共通に一般化し，組合せ的な双対性による良い特徴付けを与えた．さらにLovász（1980）は，「マトロイド・マッチング問題」への帰着を通じてこの問題が効率的に解けることを示した．

 群ラベル付きグラフにおける「非零Aパス詰め込み」は，上記の「内点素Aパス詰め込み」を含む問題であり，曲面上に埋め込まれたグラフにおける縮約不能閉路の詰め込みなど，理論的に興味深い問題を共通に一般化している．この問題はChudnovsky ら（2006）によって導入され，同論文でその良い特徴付けが，Chudnovskyら（2008）により効率的な組合せ的アルゴリズムが提案されていた．

 本研究では，組合せ最適化の分野におけるこの問題の位置づけを明らかにすべく，Lovász（1980）の結果を拡張する形で「マトロイド・マッチング問題」への帰着を与え，既知の良い性質がその帰着を通じて理解できることを示した（Tanigawa-Yamaguchi 2016）．さらに，マトロイド・マッチングの中でもとりわけ性質の良い特殊ケースである「線形マトロイド・パリティ問題」への帰着を通じて高速に解けるための，群に対する必要十分条件を明らかにし，実際に多くの群がその条件を満たしていることを示した（Yamaguchi 2016）．

（2）2ラベル禁止パスの発見
 （1）で明らかになった非零パス（1つのラベルを禁止する制約）の扱いやすさを受け，任意の2つのラベルを禁止して2点間のパスを発見する問題を導入し，その問題に対する多項式時間アルゴリズムを提案した（Kawase-Kobayashi-Yamaguchi 2015）．この問題は，無向グラフにおける「2点素パス問題」を一般化しており，非常に難しい問題であると予想されたが，Seymour（1980）による2点素パスの存在に関するグラフの幾何的な特徴付けをうまく利用・拡張することで，上記の結果を得た．