(邦訳:暗号プロトコルに対する現実的な解析)
| 竹部 裕俊 金沢大学 博士研究員 |
[背景]共通鍵暗号方式に対する暗号文改ざん攻撃の存在
[問題]暗号化鍵を何度も繰り返して使う現実的状況の設定
[貢献]現実的状況での改ざん耐性の定義と暗号方式の提案
このような攻撃を防ぐために暗号方式に求められる性質が「暗号文改ざん耐性」である.ただし,ここでは「復号結果を操作する改ざん攻撃」のみを考慮し,それに対する耐性を暗号文改ざん耐性と呼ぶことにする.共通鍵暗号方式の暗号文改ざん耐性に関しては,さまざまな攻撃者を想定した定義の提案とこれらの分類がされてきているが,本研究では攻撃者の計算能力を制限しない場合の定義に着目する.
共通鍵暗号方式の場合,暗号化と復号に使う鍵は送信者と受信者だけの秘密にしなければならない.したがって事前に鍵をお互いに共有し,場合によってはその鍵を更新(再共有)する必要がある.鍵の共有にはコストや手間がかかるため,現実的な視点からすれば,鍵を一度共有したらそれを何度も繰り返し使える方が効率の面で望ましいと考えられる.このような状況下で先ほどの暗号文改ざん攻撃を行う場合,攻撃者が同じ鍵で暗号化された暗号文を複数手に入れられることになるが,従来の暗号文改ざん耐性の定義は鍵を一度だけしか使わない場合を想定したものであるため,それが満たされたからといって今回の状況下での暗号文改ざん耐性を保証することができない.
そこで本研究では,より現実的な状況下での暗号文改ざん耐性を新たに定式化する.具体的には,暗号化鍵を何度も繰り返して使う場合を想定し,従来の定義を拡張して暗号文改ざん耐性の定義を行う.また,この拡張した暗号文改ざん耐性を満たす暗号方式を具体的に構成する.さらに本研究では,この拡張した暗号文改ざん耐性を満たすための鍵長の下界を求める.鍵の長さは暗号化および復号の計算時間に直接関わってくるため,暗号方式を構成する上で非常に重要な考察であるといえる.
[問題]暗号化鍵を何度も繰り返して使う現実的状況の設定
[貢献]現実的状況での改ざん耐性の定義と暗号方式の提案
この研究は,共通鍵暗号方式における「暗号文改ざん耐性(=頑強性)」について深く考察したものである.
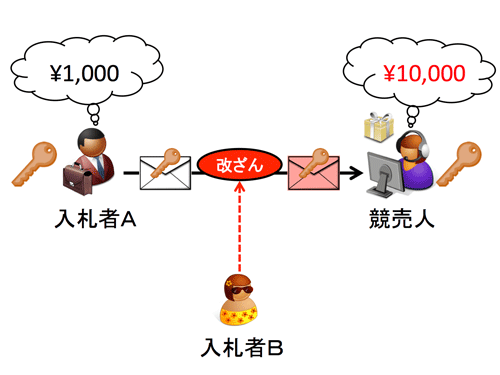
暗号方式にとって,暗号文から元の平文の情報が得られないこと(=秘匿性)は必須条件ともいえる重要な性質であるが,それだけ十分ではないことがよく知られている.たとえばインターネットオークションにおいて,入札者が入札額を暗号化して競売人に送る状況を考える.このとき,暗号方式が秘匿性を持っていれば,悪意を持った入札者Bは他の入札者Aの入札額の暗号文から元の入札額を知ることはできないであろう.しかしながら,この入札者Bはその暗号文を改ざんすることで,復号結果(=競売人に伝わる入札者Aの入札額)を操作できてしまうかもしれない.
暗号方式にとって,暗号文から元の平文の情報が得られないこと(=秘匿性)は必須条件ともいえる重要な性質であるが,それだけ十分ではないことがよく知られている.たとえばインターネットオークションにおいて,入札者が入札額を暗号化して競売人に送る状況を考える.このとき,暗号方式が秘匿性を持っていれば,悪意を持った入札者Bは他の入札者Aの入札額の暗号文から元の入札額を知ることはできないであろう.しかしながら,この入札者Bはその暗号文を改ざんすることで,復号結果(=競売人に伝わる入札者Aの入札額)を操作できてしまうかもしれない.

このような攻撃を防ぐために暗号方式に求められる性質が「暗号文改ざん耐性」である.ただし,ここでは「復号結果を操作する改ざん攻撃」のみを考慮し,それに対する耐性を暗号文改ざん耐性と呼ぶことにする.共通鍵暗号方式の暗号文改ざん耐性に関しては,さまざまな攻撃者を想定した定義の提案とこれらの分類がされてきているが,本研究では攻撃者の計算能力を制限しない場合の定義に着目する.
共通鍵暗号方式の場合,暗号化と復号に使う鍵は送信者と受信者だけの秘密にしなければならない.したがって事前に鍵をお互いに共有し,場合によってはその鍵を更新(再共有)する必要がある.鍵の共有にはコストや手間がかかるため,現実的な視点からすれば,鍵を一度共有したらそれを何度も繰り返し使える方が効率の面で望ましいと考えられる.このような状況下で先ほどの暗号文改ざん攻撃を行う場合,攻撃者が同じ鍵で暗号化された暗号文を複数手に入れられることになるが,従来の暗号文改ざん耐性の定義は鍵を一度だけしか使わない場合を想定したものであるため,それが満たされたからといって今回の状況下での暗号文改ざん耐性を保証することができない.
そこで本研究では,より現実的な状況下での暗号文改ざん耐性を新たに定式化する.具体的には,暗号化鍵を何度も繰り返して使う場合を想定し,従来の定義を拡張して暗号文改ざん耐性の定義を行う.また,この拡張した暗号文改ざん耐性を満たす暗号方式を具体的に構成する.さらに本研究では,この拡張した暗号文改ざん耐性を満たすための鍵長の下界を求める.鍵の長さは暗号化および復号の計算時間に直接関わってくるため,暗号方式を構成する上で非常に重要な考察であるといえる.
(2013年6月13日受付)

