災害時支援物資配送計画へのCMOSアニーリングの適用
1.CMOS アニーリングとは
CMOSアニーリングは,大規模な組合せ最適化問題を効率良く解くために日立が開発を進めている最適化技術である[1,2,3,4].CMOSアニーリングは,従来のノイマン型コンピュータとは異なり,磁性体のモデルの1つであるイジングモデルにおいてエネルギー関数であるハミルトニアンが最小となる状態(基底状態)を探索することで最適化計算を行う.イジングモデルの基底状態が組合せ最適化問題の最適解に対応する.図1はイジングモデルとその概念図である.青と赤の矢印はそれぞれ上向きスピン,下向きスピンを表しており,式中のに対応している.それはすなわち最適化問題におけるバイナリ変数に対応している.丸を互いに繋ぐ黒い線は変数間の結合(式の和の取り方で決まる)を意味しており,その強度が式の第一項の\( J_{ij} \)に対応している.第二項はイジングモデルにおいて外部磁場の作用を表し,他の変数とのかかわりを考慮しなくてもよい項である.第二項のみで構成されるモデルであれば,線形計画問題の手法で解くことが可能である.一見すると単純なモデルだが,問題に応じて係数値を適切に設定することで,さまざまな問題に展開することが可能である.
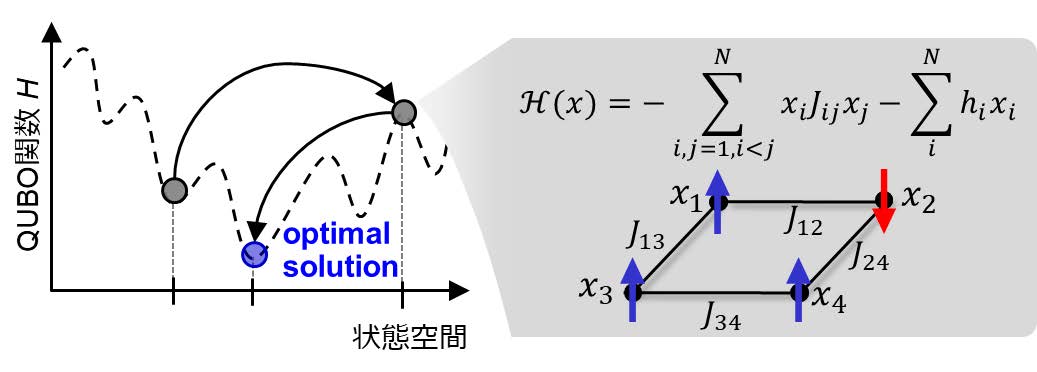
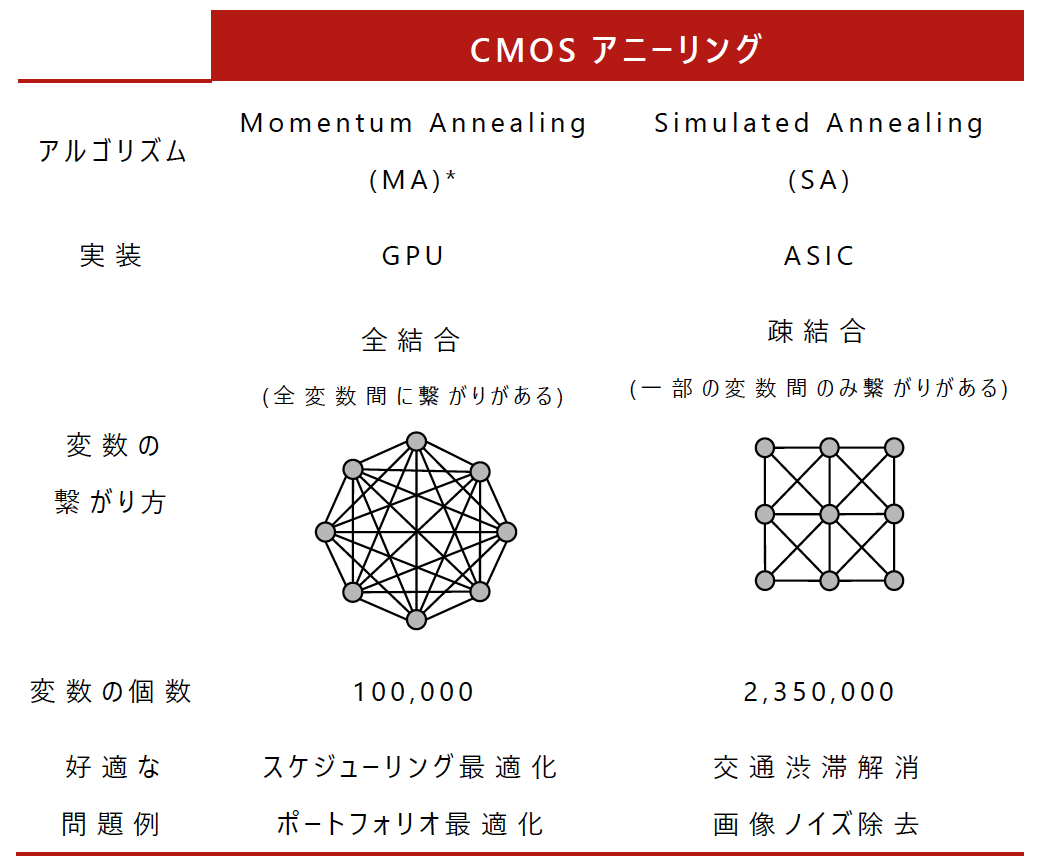
CMOSアニーリングの実装形態は2種類あり,GPUに日立独自のアルゴリズムであるMomentum Annealing[1]を実装したタイプと,専用ハードにSimulated Annealingを実装したタイプ[2,3,4]が存在する.表1に2つの実装形態をまとめた.問題に応じて適した実装形態を使い分けることが可能である.専用ハードのCMOSアニーリングは,図1のように,2つの変数間の結合が互いに隣接する場合を想定した実装となっている.モデルの形状が限定される反面,隣接のみという特徴を活かした規模の拡張が容易であり,235万変数の問題を取り扱い可能である.一方,GPUタイプのCMOSアニーリングは2変数間であればどのような結合の形態でも受け入れ可能な全結合タイプになっている.こちらはGPUのメモリ容量で取り扱い可能な問題規模が決定され,たとえばNVIDIA-V100では約10万変数となる.次章で示すとおり,本研究で取り扱う救援物資配送計画の数理モデルは集合被覆問題であり,ほかの実問題[5]で取り扱われるモデル同様,隣接スピン間の相互作用のみでは記述できない密結合のモデルであるため,GPUタイプを選択した.
2.支援物資配送計画へのCMOSアニーリング適用
本章では,救援物資配送計画問題の概要を説明する.次にCMOSアニーリングで本問題を解くための候補生成および定式化を説明する.
2.1 問題設定
本輸送計画プログラムで対象とする計算条件の概略を図2に示す.図2のST0,ST1はそれぞれ被災地の供給拠点であり,被災地外から輸送された支援物資が備蓄されているものとする.供給拠点ST0およびST1から各避難所\( \{ \text{ST}2, \text{ST}3, \dots, \text{ST}{82} \} \)に輸送機材を用いて支援物資を輸送する計画を立案した.求められる条件および要件に関して,以下の各節に記述する.
![図2 救援物資配送計画における交通網の概念図[6]](../62/DP62-S05/image/S05-fig02.jpg)
2.1.1 インフラ網(道路ネットワーク)と輸送拠点等
拠点の種類は,供給拠点と避難所の2種類として,インフラ網上のノードとして規定される.なお,各輸送機材の初期位置は供給拠点と同一とするが,2カ所ある供給拠点のどちらに輸送機材を設置するのかは,輸送機材ごとに設定可能とする.また,輸送のインフラ網(道路ネットワーク)は所与とし,各拠点等間の移動時間(距離)は所与とする.
2.1.2 輸送機材
輸送機材(輸送機材)の最大積載重量を輸送機材ごとに設定可能とする.輸送機材の総数は10台とし,本研究ではすべての輸送機材は2トントラックとした.輸送機材は初期位置である供給拠点で物資を積載し,避難所へのミルクラン方式での配送を経て,初期位置に戻らないものとする.ミルクランとは,1台の車両で複数の調達先を巡回する集荷方法を指すが,本稿では供給拠点で積載した物資を複数の避難所を巡回し配送することを指すものとする.なお,一度配送を終えた輸送機材は,再度,配送は行わないものとする.
2.1.3 救援物資
避難所が要請する対象物資の総量は,前節で示した全輸送機材が1回のミルクランでは賄えないほど大きな需要であることを前提とする.ただし,ミルクランによる輸送を行うため,各避難所の要請量は輸送機材の最大積載量に満たない要請量とする.本研究では,要請量到達まで0.5トンのところまではすでに配送済みであるとした.
- 個別の輸送機材に対して物資の載荷量は最大積載重量を上限とする.
- 出荷元となる供給拠点には,物資が無限量,備蓄されているものとする.
2.1.4 評価値
本件で最適化の対象となる評価値は,「輸送距離」と,「避難所の平等性」とする.「輸送距離」は,各輸送機材が供給拠点から出発し,ミルクランの最後の避難所で荷降ろしを終了するまでの輸送距離を対象とし,全輸送機材の総和とする.以下,「避難所の平等性」について説明する.平等性とは,基礎自治体(市区町村)間の平等性を対象とする.すなわち,各基礎自治体の充足率を揃えることを意味し,各基礎自治体の充足率 \( Y^c \)は,要請量 \( W_\text{demand}^c\ \)に対する供給済み量 \( W_\text{supplied}^c \) と供給量 \( W^c \) の和で定義される.なお,避難所は,1つの基礎自治体に属し,基礎自治体の要請量,供給量は,所属する避難所の要請量,供給量の総和で求められる.以下は,平等性を示す指標である充足率の標準偏差 \( \sigma \) の例である.
\[ \sigma = \sqrt{\frac{1}{N_{\text{city}}} \sum_{c} \left( Y^c - \frac{\sum_{c} Y_c}{N} \right)^2}, \quad Y^c := \frac{W_{\text{supplied}}^c + W^c}{W_{\text{demand}}^c} \]
ここで, \( N_\text{city} \) は基礎自治体の総数である.基礎自治体間の平等性が増すと, \( \sigma \) は小さな値となり,平等性が完全に満たされる場合 \( \sigma=0 \) となる.
2.2 手法および定式化
本研究で用いた手法の大枠は次のようになる.
Step1)制約を考慮して経路候補を生成する(2.2.1項)
Step2)生成された経路候補の中から,最適な経路の組合せを選択する(2.2.2項)
2.2.1 経路候補生成
本項では,経路候補生成の計算の概要について説明する.経路候補生成はCMOSアニーリングの前処理部分にあたり,次節で説明するCMOSアニーリングで計算する数理モデルの係数を算出する部分である.経路候補生成は,アニーリング型計算機に限らず,数理最適化ソルバを効率的に使いこなすための前処理として,鉄道計画などの複雑な制約条件を持つ問題でたびたび用いられている[7].経路候補生成の処理は,CMOSアニーリングに限らず,アニーリング型計算機が苦手とする制約条件や,そもそも数式で表現できない制約条件等を効率的に取り込むために有効である.また,アニーリング型計算機が扱うことができる問題規模には限りがあり,計算機のメモリサイズに合わせて問題規模を事前に削減することは,そもそもの計算を成り立たせること,計算速度向上の両面で有効である.この前処理部ではドメイン知識やグラフ解析の知見等を活かした問題削減を行うことで,問題サイズを調整することも可能である.本研究では,図2に示すような供給拠点および避難所間の道路の接続をグラフ化した道路ネットワーク上で,輸送機材1台あたりの経路のパターンを探索し,その輸送機材の経路候補として列挙した.その際に,解として妥当でない非常に長距離の経路および,非効率な順序で避難所を訪問するルートを事前に削除することで変数を削減した.本研究で扱う道路は,すべての避難所および供給拠点が接続されており平常時に近いものであるが,災害時に道路が寸断されるなどして通行不可能な道路が発生した際は,入力データで道路のつながりがないように書き換えることで対応できる.
各経路候補 \( {j} \) で供給拠点 \( {k} \) から出発する場合は \( {P}_{\ {kj}}=\mathbf{1} \) ,そうでなければ \( {P}_{\ {kj}}=\mathbf{0} \) ,避難所 \( {i} \) を訪問する場合は \( {A}_{\ {ij}}=\mathbf{1} \) ,そうでなければ \( {A}_{\ {ij}}=\mathbf{0} \) として列挙すると,図3のような形で候補が列挙される.経路候補列挙の際は,CMOSアニーリングの数式で用いる移動距離(図3の \( {D_j} \) ) や供給量(図3の \( {W_j^c} \) )を算出する.経路候補算出の時点では単独の経路についてしか考慮できないため,複数の輸送機材にまたがる制約やKPIを考慮するには次節で説明するCMOSアニーリングによって組合せ問題を解く.
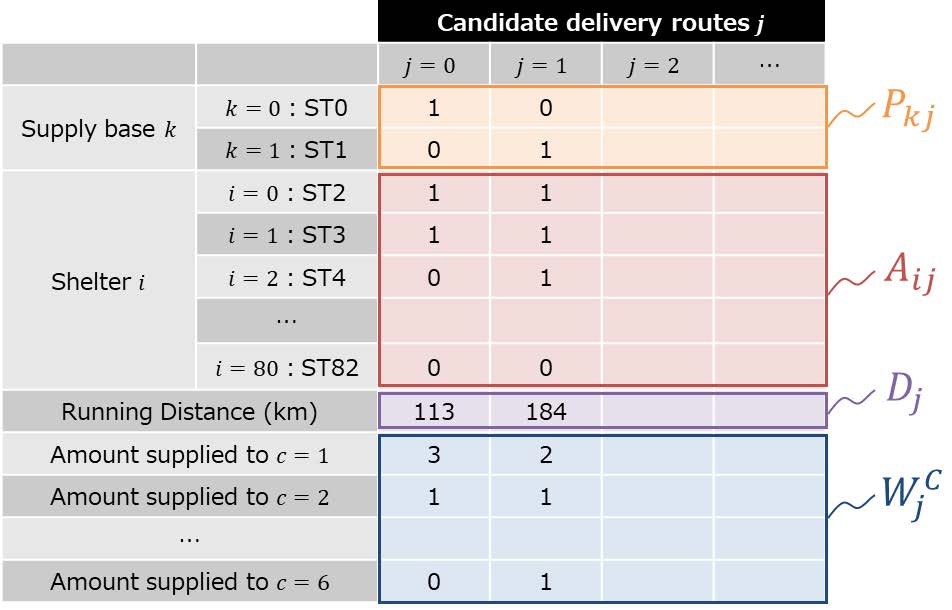
表2には経路候補生成に要する計算時間と問題規模の目安を示す.3章で示す結果データとは異なるスピン数であるが,同程度のスピン規模であれば計算時間に差はないことを確認できている.この処理にかかる時間は次節で示されるアニーリング時間と比較しても十分に小さいので,計算フロー全体で評価しても経路候補生成の処理はボトルネックとはならない.

2.2.2 定式化
前節で生成した経路候補表から最適な経路を求める問題は,物資の不足量を表す式(2.1),輸送機材の総走行距離を表す式(2.2),基礎自治体間の物資不足量平準化を表す式(2.3)を目的関数に持ち,式(2.4)で表される輸送機材制約および式(2.5)の訪問回数制約を制約条件に持つ集合分割問題として定式化した.
\[\left(\sum_{c} W_\text{demand}^c-\sum_{c} W_\text{supplied}^c\right)-\sum_{c}\sum_{j}{W_j^c x_j}\] | (2.1) |
\[\sum_{j}{D_jx_j}\] | (2.2) |
\[\sigma=\sqrt{\frac{1}{N_\text{city}}\sum_{c}\left(Y^c-\frac{\sum_{c} Y_c}{N_\text{city}}\right)^2}, \quad Y^c := \frac{W_\text{supplied}^c+W^c}{W_\text{demand}^c}\] | (2.3) |
\[\sum_{j} P_j x_j = N_{\text{truck}}^k\] | (2.4) |
\[\sum_{j} A_{ij} x_j \leq 1\] | (2.5) |
\( A_{ij} \) は経路候補表で与えられる 0/1 の定数値であり,添え字 \( i,j \) はそれぞれ行番号,列番号である.変数 \( x_j \) は \( \ j \) 番目の割当候補を選択するか否かを表しており,選択する場合は \( x_j=1 \) ,しない場合は \( x_j=0 \) となる.今回の定式化では避難所の所在地ごとにグループを作成し基礎自治体とした. \(N_\text{city}\) は総基礎自治体数を表す.式(2.1)における \(W_\text{demand}^c\) は基礎自治体 \(c\) の物資の総要求量である. \(W_\text{supplied}^c\) は基礎自治体 \(c\) の避難所に供給済みである物資の総量である.すなわち, \(W_\text{demand}^c-W_\text{supplied}^c\) が基礎自治体 \(c\) の物資の不足量である. \(W_j^c\) は供給経路候補 \(j\) を選択した際の基礎自治体 \(c\) への物資供給量である.式(2.1)は,全体の物資の不足量と物資の供給量の差を表す.式(2.2)中の \(D_j\) はそれぞれ供給経路候補 \( j\) を選択した場合の輸送機材の走行距離である.式(2.2)はすべての輸送機材の総走行距離を表す. \(Y^c\) は式(2.3)の定義のとおり,基礎自治体 \(c\) の物資要求量に対する物資不足量の比率(充足率)である.式(2.3)は基礎自治体ごとの充足率の分散を表す.
式(2.4)は輸送機材数制約である. \(N_\text{truck}^k\) は供給拠点 \(k\) から出発可能な輸送機材数であり,等式が成立するとき,解は実際に運用可能である.この制約条件を満たし,式(2.5)を満たさない解を「実行可能解」と呼ぶ.式(2.5)は訪問回数制約である.各避難所への訪問回数が2回以上とならないことを表す.この制約を満たさない場合でも運用は可能であるため,式(2.4)よりも弱い制約である.式(2.4)を満たし,かつ式(2.5)を満たす解を「制約充足解」と呼ぶ.この最適化問題をCMOSアニーリングによって求解する方法を示す.CMOSアニーリングでは,目的関数を最小化する最適化問題を,イジングモデルの最低エネルギー状態探索に当てはめる.集合分割問題を解くためのモデルのハミルトニアン(エネルギー関数)は,次のようになる.
\( \mathcal{H} = -\alpha_1 \sum_c \sum_j W_j^c x_j + \alpha_2 \sum_j D_j x_j + \alpha_3 \sum_c \left( Y^c - \frac{\sum_c Y_c}{\text{N}_{\text{city}}} \right)^2 \\ \hspace{6em} + \alpha_4 \left( \sum_j P_j x_j - N_{\text{truck}}^k \right)^2 + \alpha_5 \sum_i \left( \sum_j A_{ij} x_j \right) \left( \sum_j A_{ij} x_j - 1 \right) (2.6)\)
前述の式(2.1)〜(2.5)と同じ変数 \(x_j\) はCMOSアニーリングにおけるビットである「スピン」に対応する.スピン数は経路候補数を表し,その数は訪問回数と避難所数のみに依存する.訪問回数や避難所数が増えるとスピン数も増加する.式(2.6)中の第一項は式(2.1)の物資の不足量最小化(供給量最大化)の目的関数にあたる.同様に,式(2.6)中の第二項は総走行距離の最小化,第三項は充足率の分散最小化の目的関数にあたる.式(2.6)中の第四項,第五項はそれぞれ輸送機材数制約,訪問回数制約にあたる.第四項では,拠点 \(k\) から出発する輸送機材数が前提条件と同数である場合は0,異なる場合は正の有限値をとる.第五項では,避難所 \(i\) への訪問回数が0回のとき, \( \sum_{j}{A_{ij}x_j} \) が0となり,訪問回数が1回のとき, \( \sum_{j}\left(A_{ij}x_j-1\right) \) が0となる.避難所 \(i\) への訪問回数が1回より多い場合は正の有限値をとる.そのため,制約条件が満たされない場合はエネルギーが高くなり,最適解から離れる.各項の係数 \(\alpha_1,\alpha_2,\alpha_3,\alpha_4,\alpha_5\) はハイパーパラメータであり,各項に重み付けを行うことによって,どのコストを優先すべきかをユーザ定義で与えられるように用いた.
3.実験結果
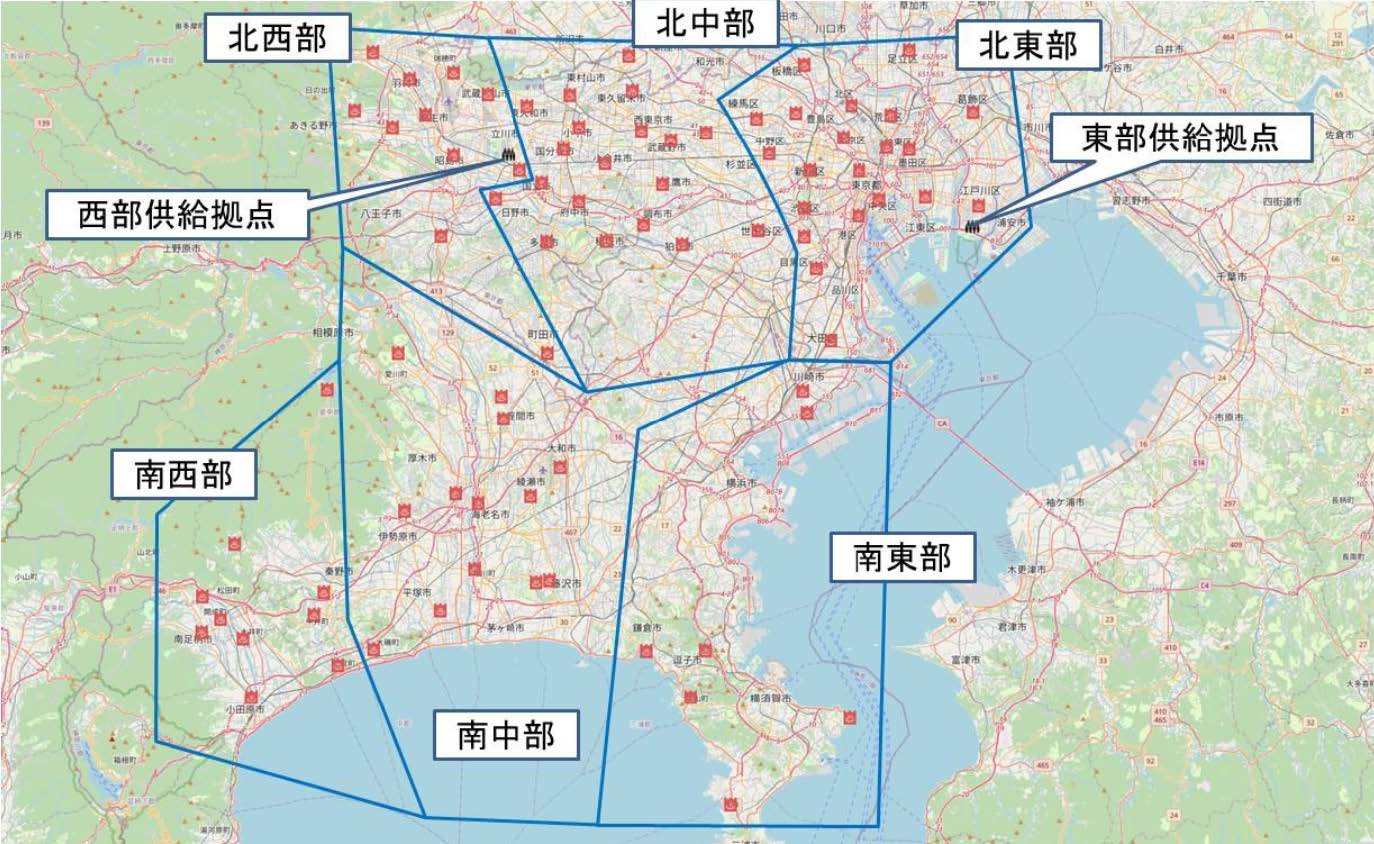
本章では,東京都江戸川区の東部供給拠点と東京都立川市の西部供給拠点の2カ所の供給拠点から,各輸送機材が東京都および神奈川県の81の避難所を複数巡回し配送する方式での救援物資配送計画を立案した結果を述べる.81の避難所は6つの基礎自治体(北東部,北中部,北西部,南東部,南中部)に属すると仮定し,東部供給拠点と西部供給拠点から5台ずつ,計10台の2トントラックが各避難所に0.5トンずつ救援物資を配送するとした.本研究で対象とした避難所と基礎自治体の区分を図4に示す.各2トントラックが2,3,4カ所の避難所を訪問する場合についてそれぞれ経路候補生成を行い,表3に示すCMOSアニーリングの入力データを作成した.表3の探索打ち切り幅は経路候補生成処理で用いた各探索での打ち切り幅を意味する.そのため,打ち切り幅が大きいものほど,スピン規模が大きくなっている.
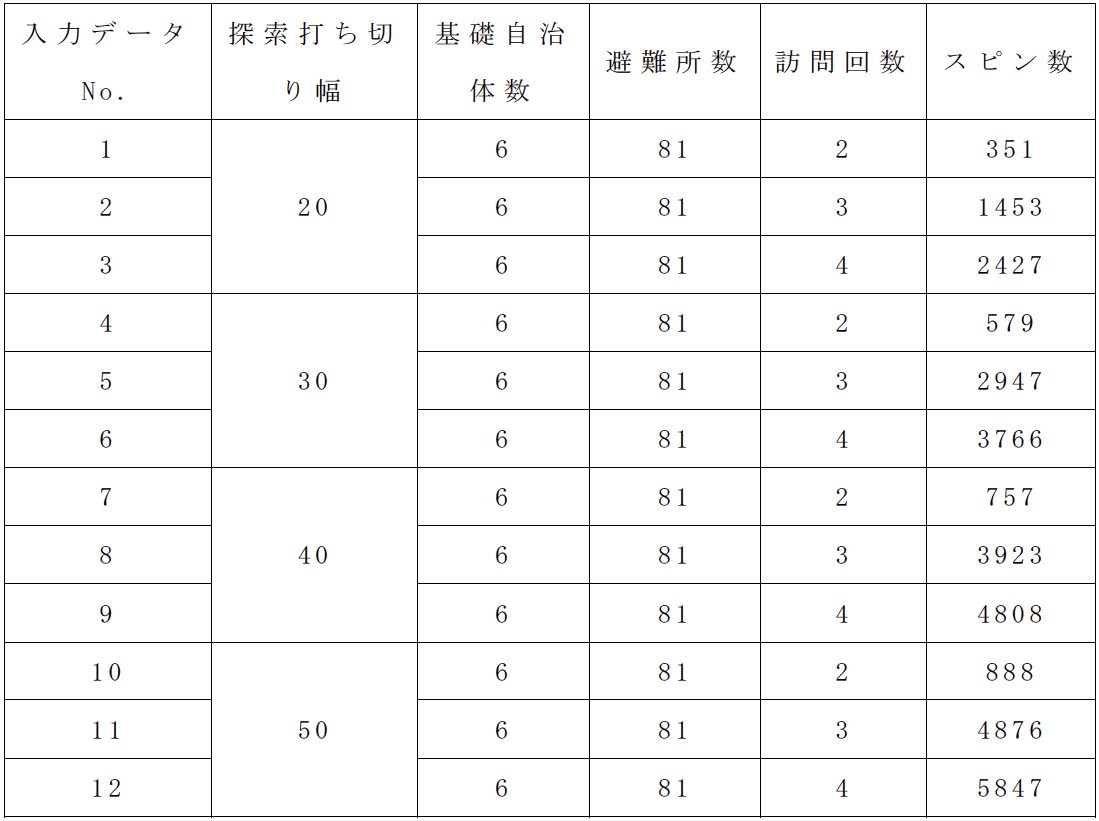
この実験データを用いてCMOSアニーリングとPyQUBOを用いたシミュレーテッド・アニーリングで実験を行った.
3.1 Simulated AnnealingとCMOS Annealingにおけるスケーラビリティの検証
CMOSアニーリング,シミュレーテッド・アニーリング(SA)ともにパラメータ設定として,スイープ数,レプリカ数(並列実行数)およびアニーリング計算回数は以下の値に設定した.
- スイープ数:1,000
- レプリカ数:100
- アニーリング計算回数:30
全スイープ数と全レプリカ数分の計算をすべて実行することを1計算とし,1計算にかかる時間をアニーリング時間とした.CMOSアニーリングの実験は社内共有GPU計算機の計算サーバー上で行った.SAの実験はPyQUBOバージョン1.0.9を用いてCPU上で実行した.ハイパーパラメータおよびアニーリング温度の設定には,(株)Preferred Networksによるオープンソースのハイパーパラメータ自動最適化フレームワークOptuna[8]を用いた.
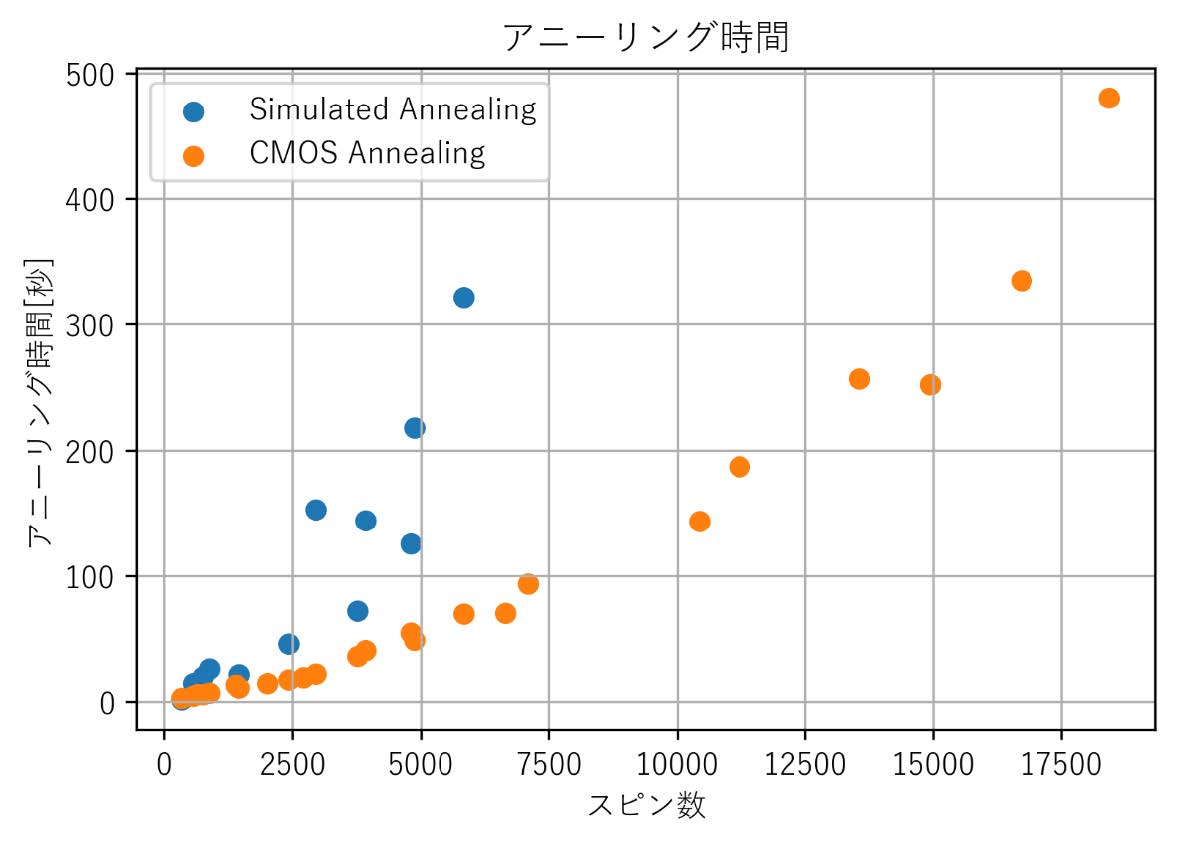
スケーラビリティの検証のため,CMOSアニーリングとSAで,各入力データに対し30回計算を行った.図5に,CMOSアニーリングとSAのスピン数に対する30回の平均アニーリング時間を示す.図5に示すように,CMOSアニーリングではSAに比べて2〜7倍程度高速に求解できるという結果が得られた.これは,SAはCPU上で逐次的に計算を実行しているが,CMOSアニーリングではGPUを用いて,並列にレプリカを計算しているためである.
3.2 ルールベースの解とCMOSアニーリングの解精度比較
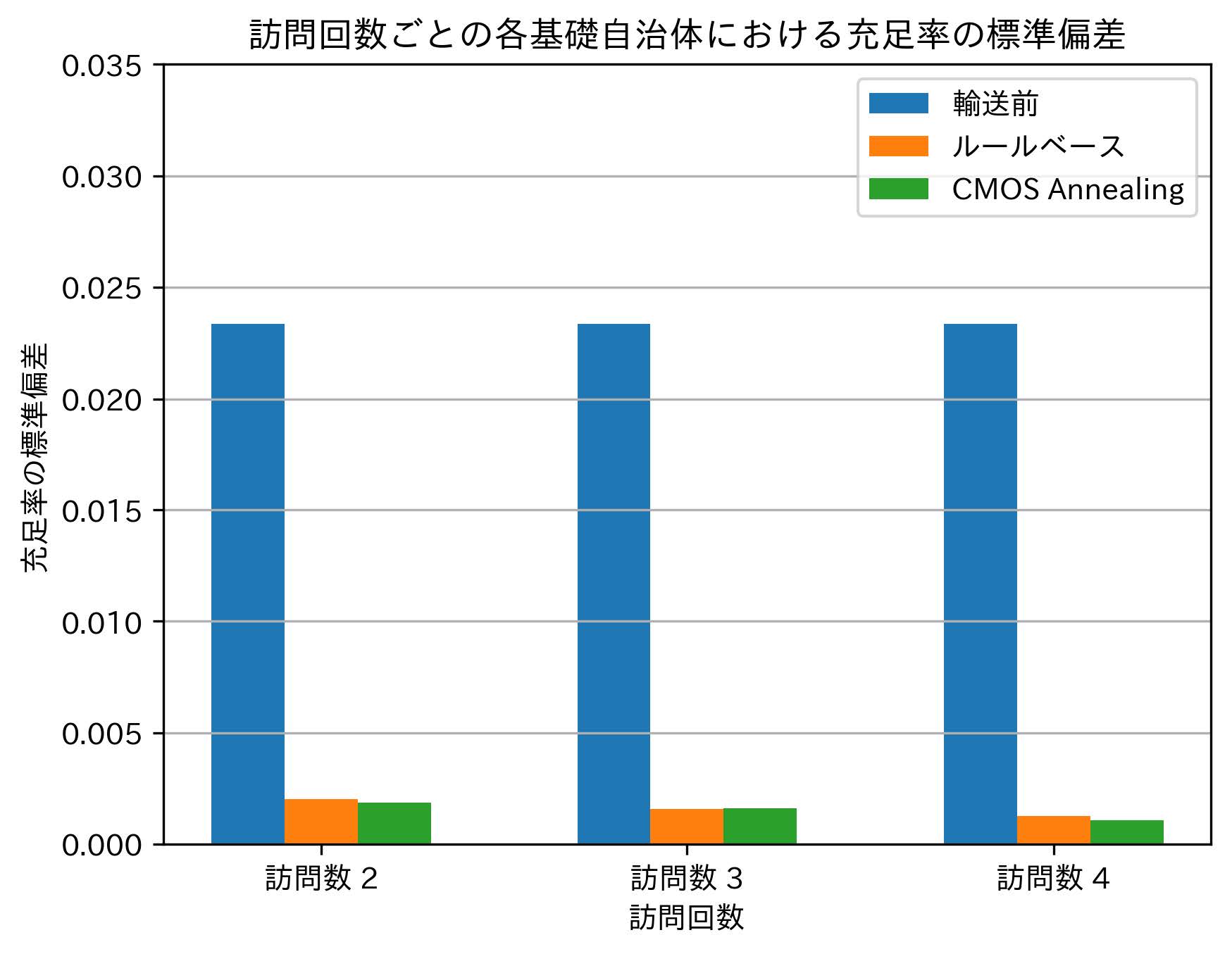
ここでは訪問回数2,3,4回,拠点数81の問題を用いてルールベースとCMOSアニーリングの比較評価を行った.基礎自治体ごとの充足率の標準偏差,輸送機材の総走行距離という2つのKPIを比較の対象とした.
ルールベースは,(国研)海上・港湾・航空技術研究所の作成したアルゴリズム[9]である.基礎自治体および各基礎自治体内の避難所を物資の充足率の低い順にソートすることで,図6に示すようなランキング表を作成し,先頭の避難所から順に各輸送機材の配送先に加えていく貪欲法を用いている.
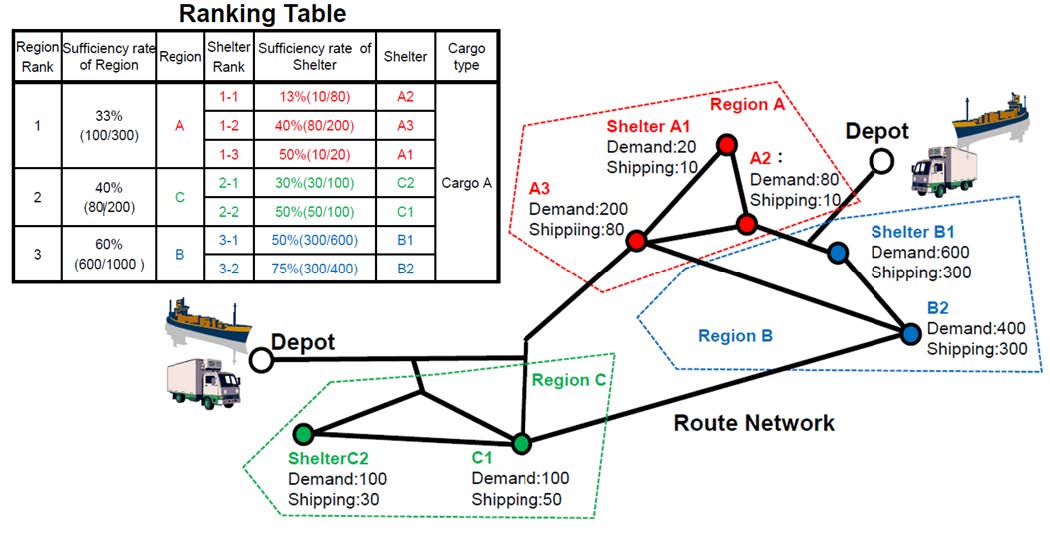
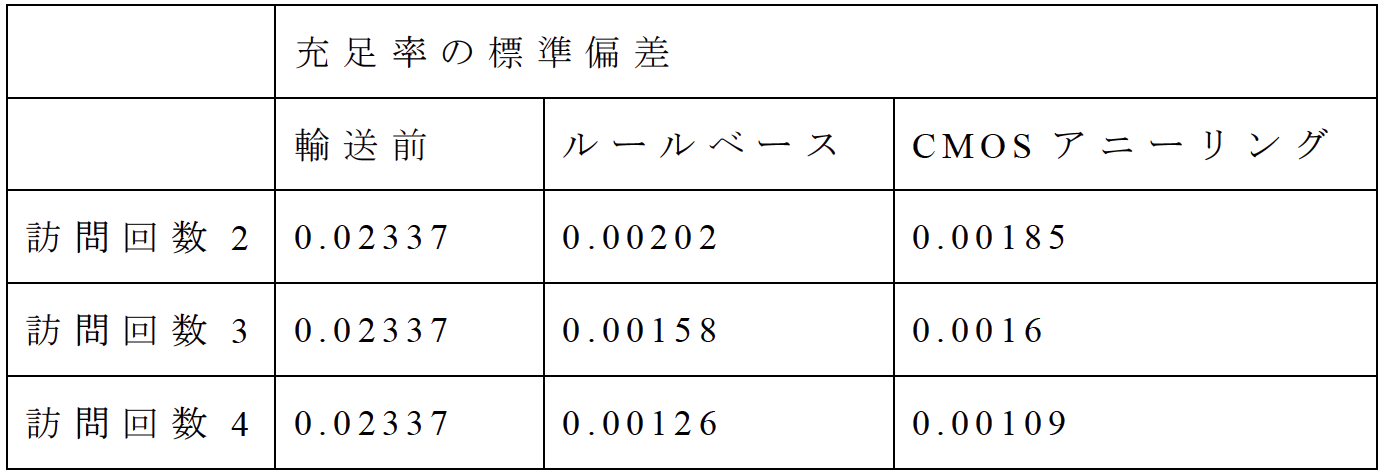
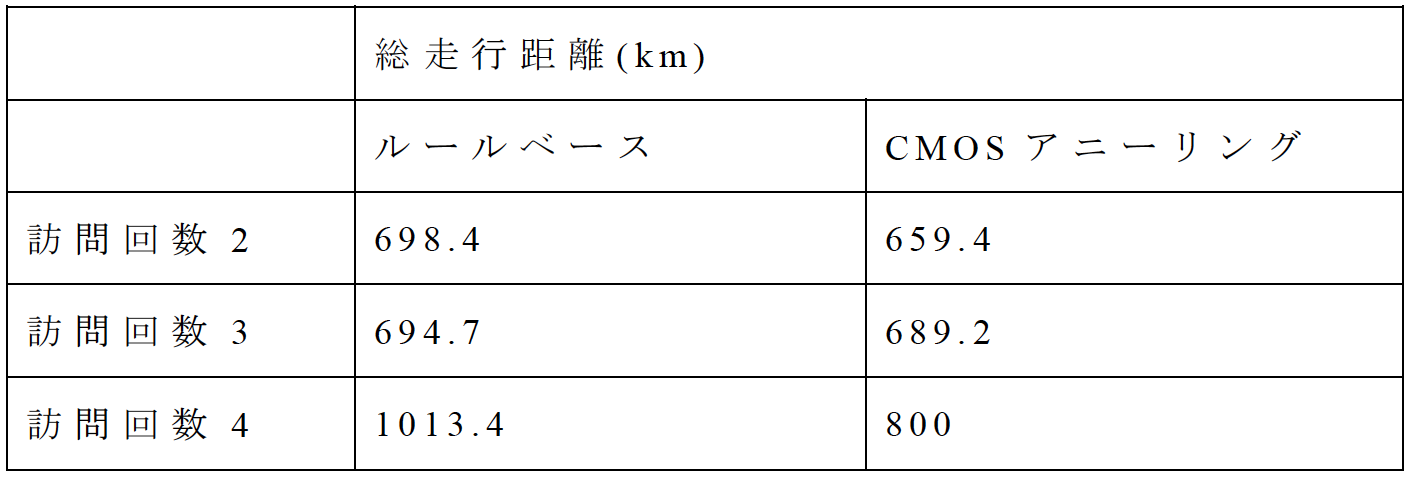
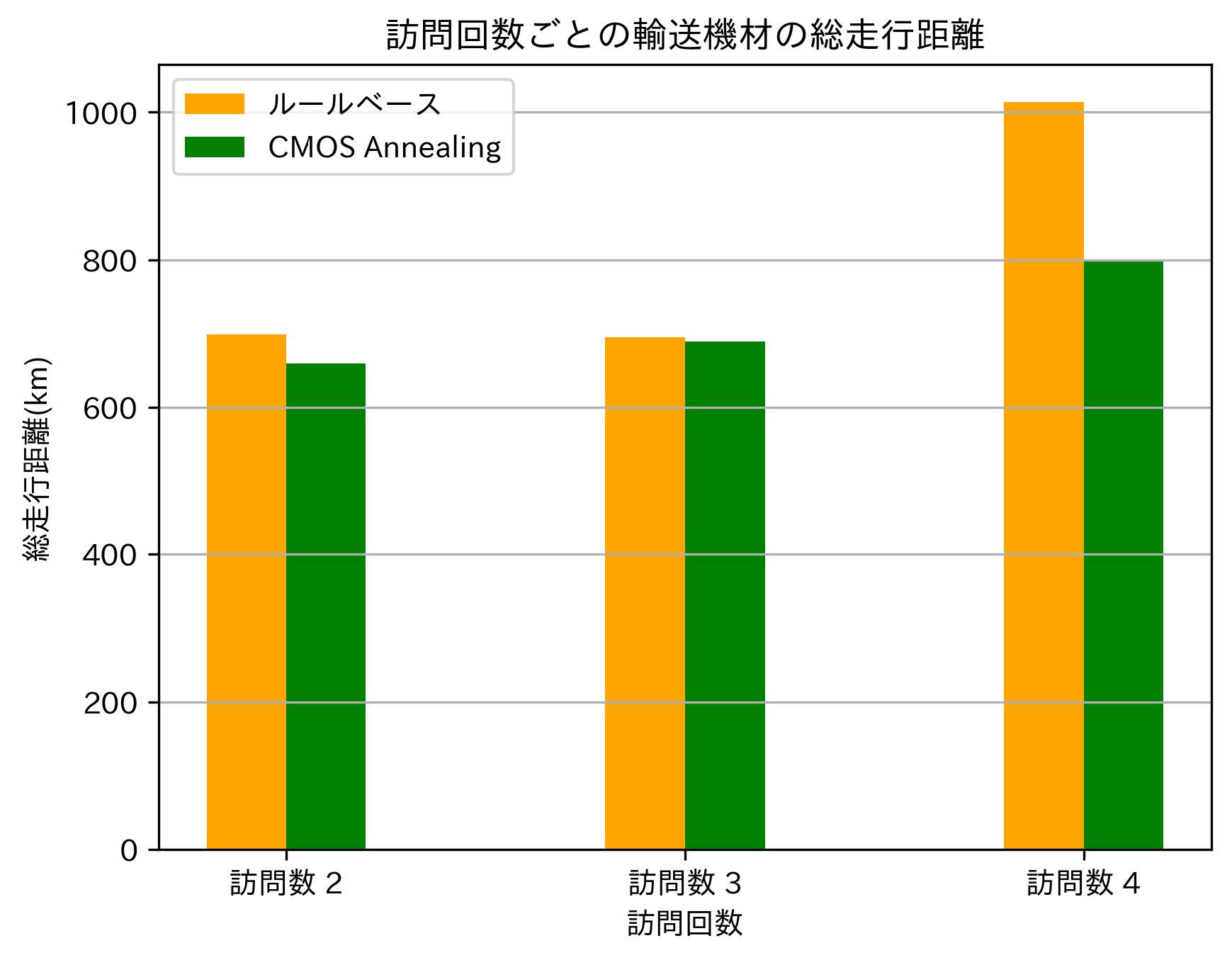
表4および図7に示す充足率の標準偏差は訪問回数2,4の実験結果において,CMOSアニーリングの解がルールベースの解よりも標準偏差が小さく,最適な解を得られていることが確認できた.表5および図8に示す輸送機材の総走行距離では,すべての訪問回数についてCMOSアニーリングの解ではルールベースの解よりも走行距離が減少していた.これより,CMOSアニーリングはルースベースと比較してより平等かつ効率的な救援物資配送計画を立案できるという結論を得た.また,定式化およびアルゴリズムの正当性について検証できた.
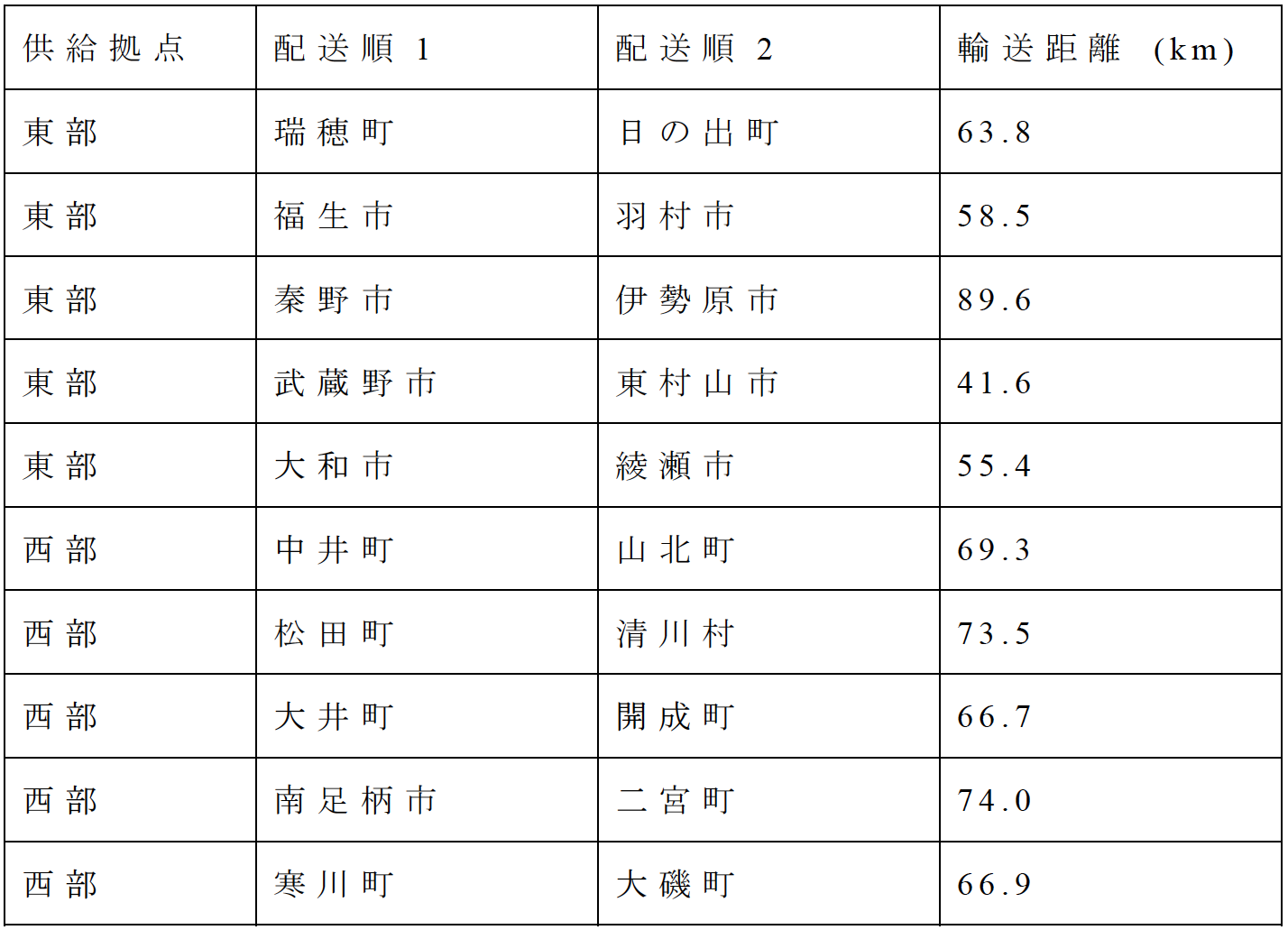
以下に,訪問回数2,3,4回のデータに対して,訪問回数ごとにCMOSアニーリングで得られた救援物資の配送順序および各基礎自治体の充足率の変化を示す(表6,図9,表7,図10,表8,図11).
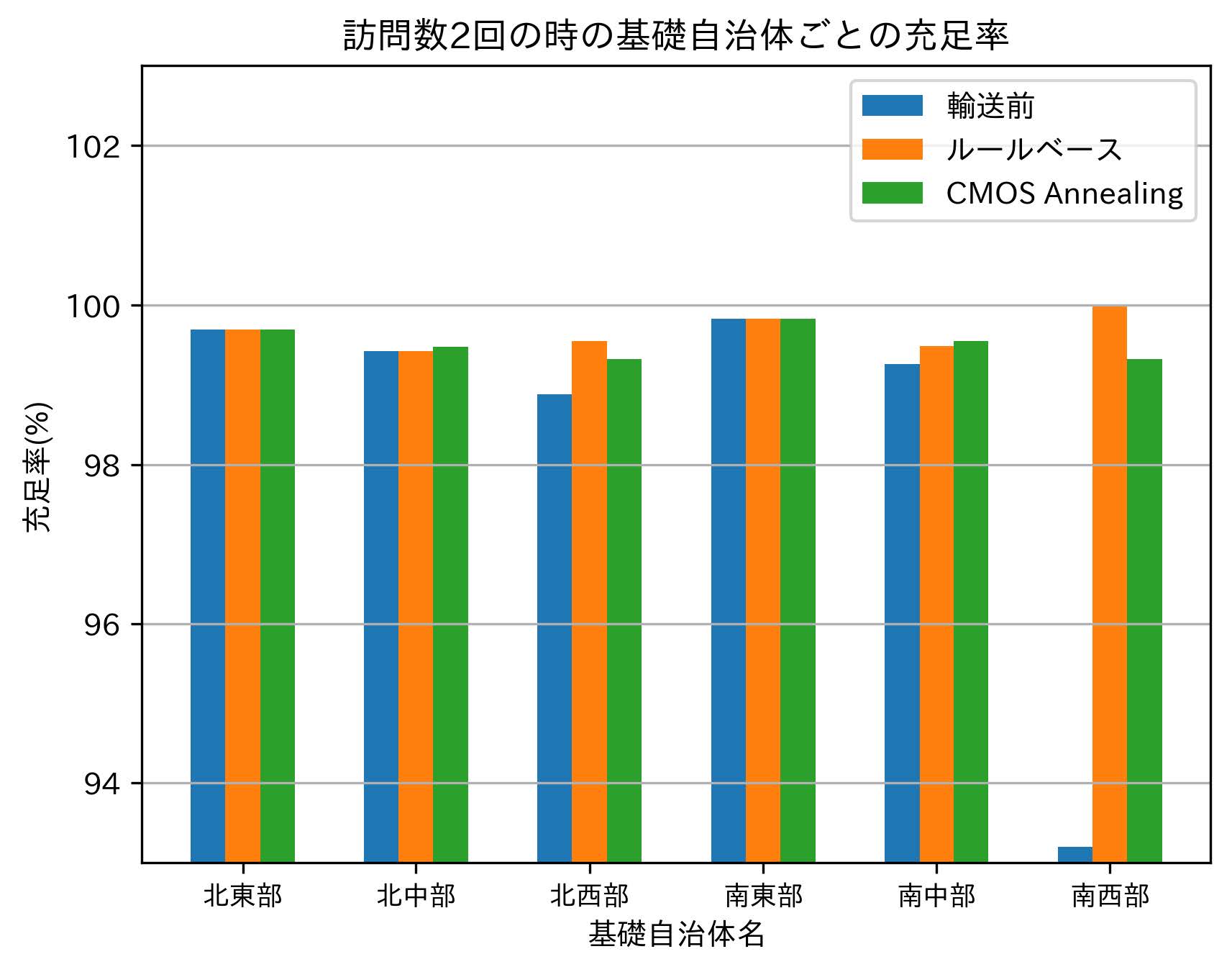
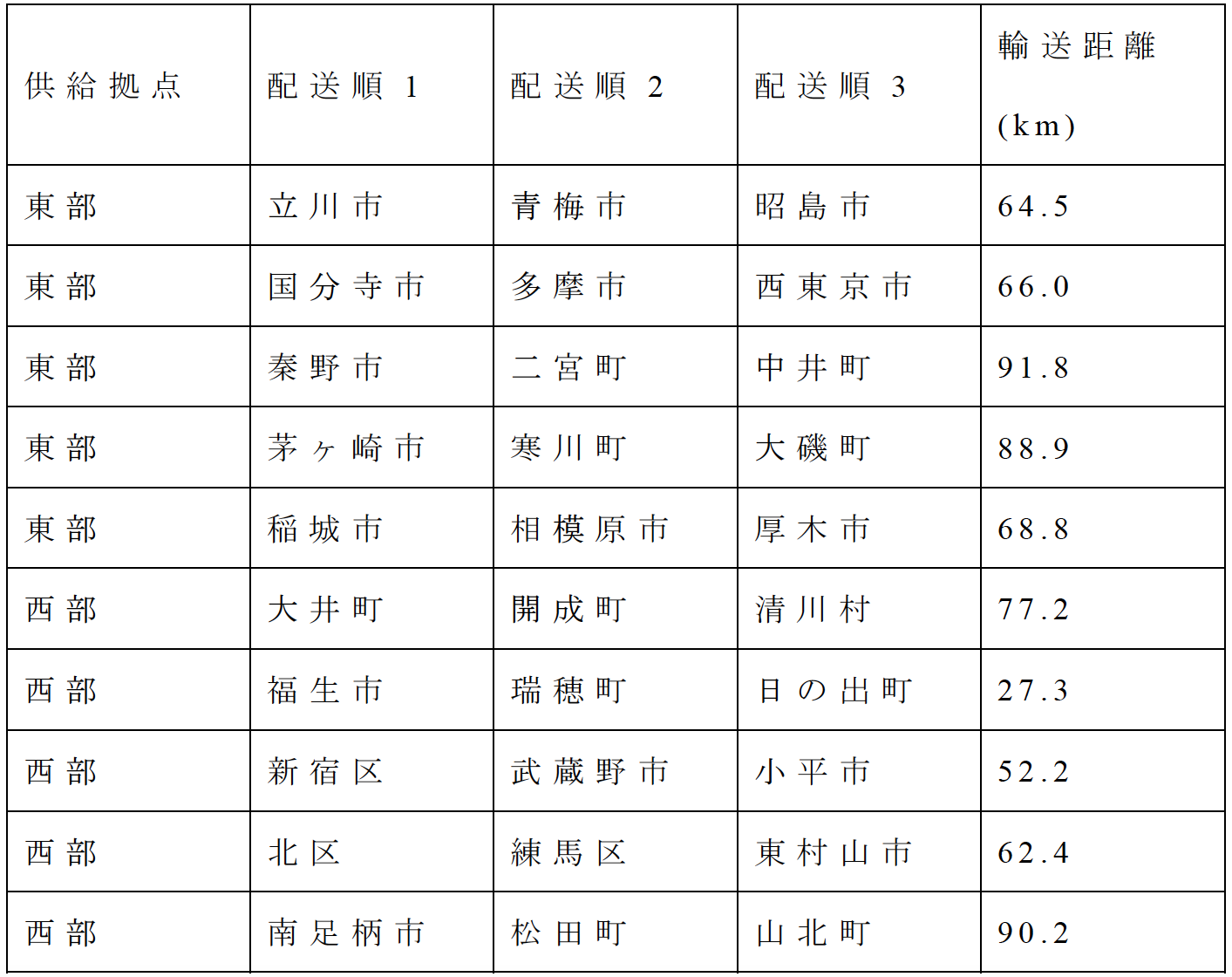
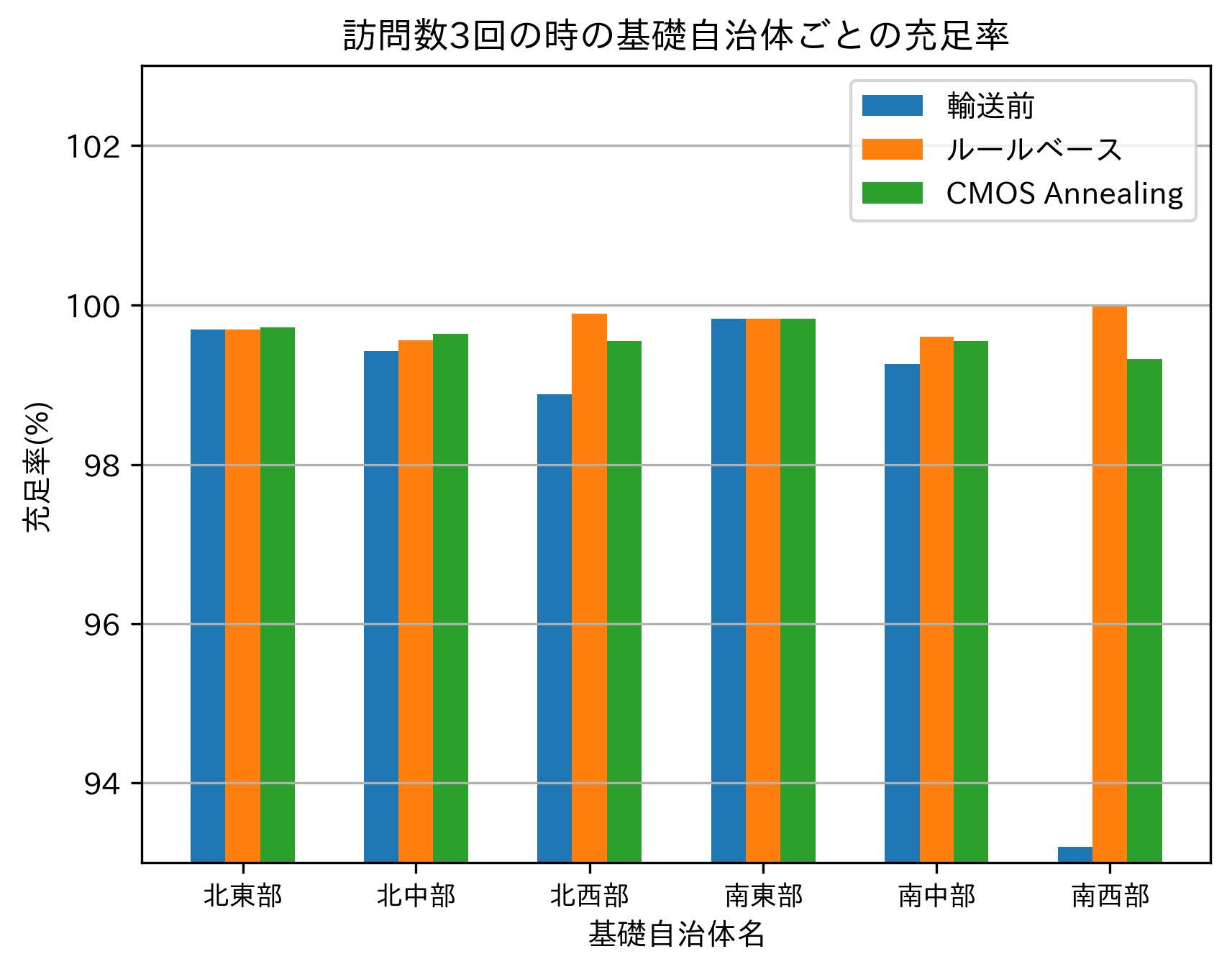
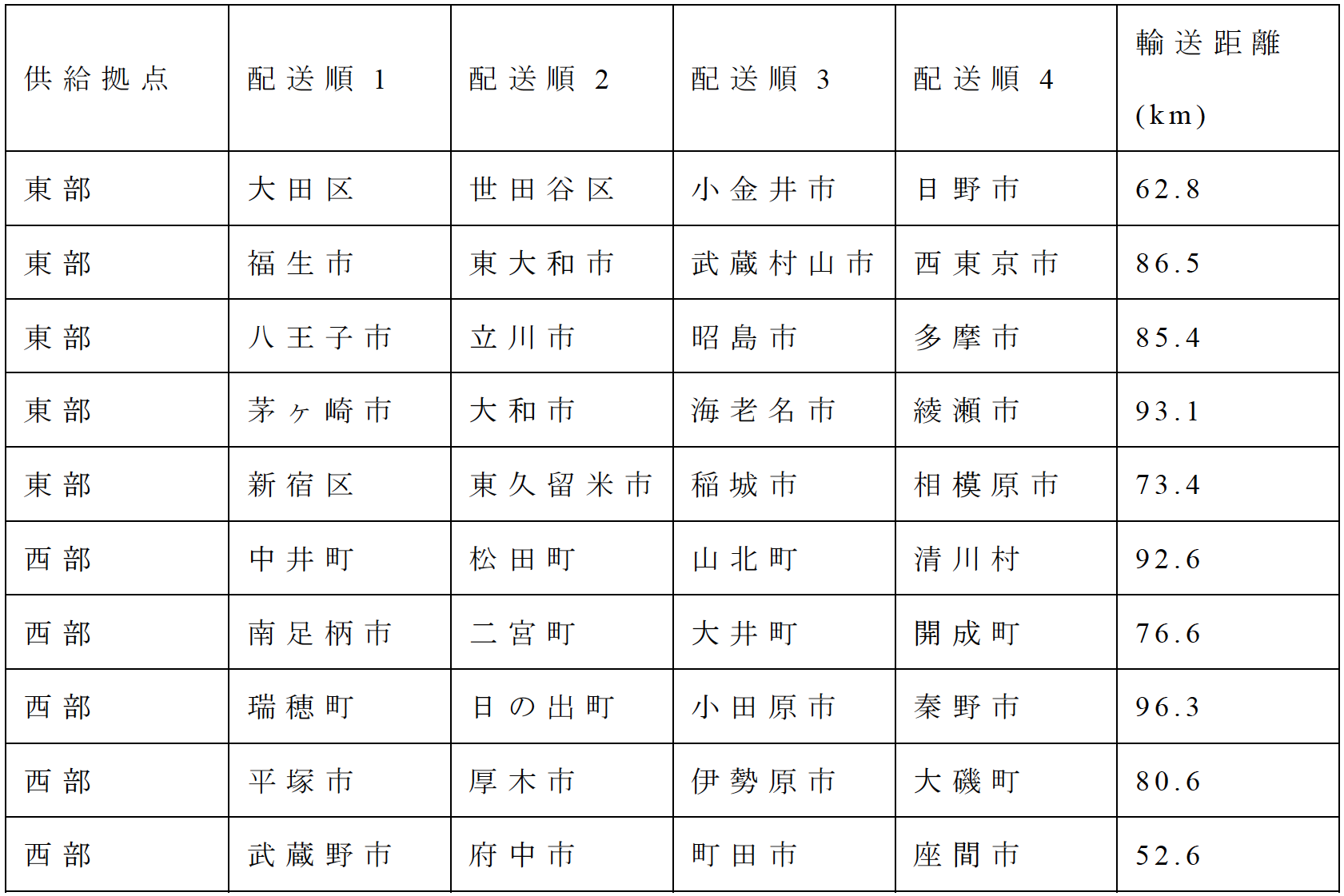
![図11 訪問数4回のときの基礎自治体ごとの充足率[6]](../62/DP62-S05/image/S05-fig11.jpg)
4.結果の検討および実用化への課題
本章では,3章の実験で得られた結果から,SAとCMOSアニーリングの比較,ルールベースの解法とCMOSアニーリングの比較とをそれぞれ行い,救援物資配送計画におけるCMOSアニーリングの適用可能性について考察する.また,実用化に向けた今後の課題について述べる.
4.1 結果の検討
まず,SAとCMOSアニーリングの比較について述べる.計算時間の比較では,逐次計算を実行しているSAと異なりCMOSアニーリングではレプリカの並列計算とスピンの同時更新[1]により,問題規模が増大しても計算時間への影響が小さく,2〜7倍高速に計算可能であることが分かった.
次にルールベースとCMOSアニーリングの比較について述べる.表4に示したとおり,各基礎自治体間の充足率の標準偏差は訪問回数2,4でCMOSアニーリングの解がルールベースの解を上回っていた.また,表5に示した輸送機材の総走行距離では,すべての訪問回数についてCMOSアニーリングの解ではルールベースの解よりも走行距離が減少していた.
ルールベースでは,物資の充足率の低い順に配送する避難所を決定し,その避難所への走行距離が最も短い輸送機材の配送先集合に避難所を加える貪欲法を用いている.このため,配送後の状況を考慮しておらず,配送後の充足率の標準偏差が大きくなっていると考えられる.一方で,CMOSアニーリングでは,配送後の充足率の標準偏差を最小化するよう目的関数を設定しているため,ルールベースと比較してより平等な解が得られたと考えられる.
また,輸送機材の総走行距離についても,ルールベースでは順に追加された配送先集合から貪欲法を用いて配送順を決定しているが,CMOSアニーリングでは候補生成の段階で,総走行距離が一定の値未満となるように入力データを生成している.CMOSアニーリングで解を求める際にも,総走行距離を最小化するように目的関数を設定しているため,貪欲法を用いたルールベースと比較して最大21%総走行距離の短い解が得られたと考えられる.
4.2 実用化への課題
今後,救援物資配送計画にCMOSアニーリングを適用するために必要な課題は以下が考えられる.
- 本研究の問題設定では1種類の物資を配送しているが,実際の災害時を想定し,輸送機材に複数の物資(水,食料等)を積載する場合の配送計画も想定する.
- 東京・神奈川の避難所を対象としたが,さらに範囲を広げる.
- 配送経路最適化の部分をメインで取り組んでいるが,実際の問題設定により近づくように計算対象範囲を広げ,輸送機材間の積み替え(例:トラックからトレーラーへの積み替え)や避難所以外の巡回(港湾利用)なども想定する.
参考文献
- 1)Okuyama, T. et al. : Binary Optimization by Momentum Annealing, Phys. Rev. E 100, 012111 (2019) .
- 2)Yamaoka, M. et al. : 20-K-Spin Ising Chip for Combinatorial Optimization Problem With CMOS Annealing, ISSCC Dig. Tech. Papers 432–433 (2015) .
- 3)Yamamoto, K. et al. : A 1.3-Mbit Annealing System Composed of Fully-Synchronized 9-board x 9-chip x 16-kbit Annealing Processor Chips for Large-Scale Combinatorial Optimization Problems, A-SSCC, pp.1-3 (2021).
- 4)Yamaoka, M. : Next Frontier across ML: Combinatorial Solution Engine with Multivariate Index for Wide-range Applications from Financial Portfolio to Work-shift Scheduling, AI EXPO 2022, Aug. 17 (2022).
- 5)(株)日立製作所:勤務シフト最適化ソリューション,金融ソリューション,https://www.hitachi.co.jp/products/it/finance/solutions/application/common/CMOS-PersonnelShift/index.html
- 6)高橋佳歩,正木晶子,荒谷太郎,間島隆博,小埜和夫:災害時の配送計画に関する疑似量子コンピュータの有効性,日本オペレーションズ・リサーチ学会 2022年秋季研究発表会&シンポジウム,新潟,日本オペレーションズ・リサーチ学会(Sep.13, 2022).
- 7)富井規雄,今泉 淳,加藤 怜:鉄道の運行計画作成の高度化に向けて 現状と課題,情報処理,Vol.55, No.1, pp.72–81 (Jan. 2014).
- 8)Akiba, T., Sano, S., Yanase, T., Ohta, T. and Koyama, M. : Optuna: A Next-Generation Hyperparameter Optimization Framework, Proceedings of the 25th International Conference on Knowledge Discovery and Data Mining (2019).
- 9)Majima, T., Aratani, T. and Hosotsubo, S. : Information Sharing System for Relief Supplies Transport Operation in the Event of Disasters, 9th International Conference on Transportation and Logistics, Incheon,T-LOG (2022).

高橋佳歩
kaho.takahashi.ut@hitachi.com
(株)日立製作所 研究開発グループ 計測インテグレーションイノベーションセンタ エッジコンピューティング研究部所属.2020年東京工業大学理学院物理学系修士課程修了.同年,(株)日立製作所入社.現在,CMOSアニーリングの研究開発に従事.

正木晶子(正会員)
akiko.masaki@ntt.com
現在はNTTソフトウェアイノベーションセンタ所属.2009年首都大学東京博士前期課程修了.2011年同大博士後期課程単位満期退学.東京大学物性研究所,理化学研究所を経て,2018年より(株)日立製作所にてCMOSアニーリングの研究に従事.2024年より現所属にてAI推論基盤の研究に従事.博士(理学).

荒谷太郎
aratani@m.mpat.go.jp
2011年博士(工学)(日本大学)取得.2014年(独)海上技術安全研究所 入所.2016年(国研)海上・港湾・航空技術研究所 海上技術安全研究所発足(組織変更).2017年~現在,知識・データシステム系 主任研究員.

間島隆博
majy@m.mpat.go.jp
1992年運輸省船舶技術研究所 入所,2009年博士(工学)(東京工業大学)取得.2016年(国研)海上・港湾・航空技術研究所 海上技術安全研究所発足(組織変更).2017年~現在,知識・データシステム系 系長.

小埜和夫
kazuo.ono.ap@hitachi.com
2006年に(株)日立製作所の中央研究所に入所.大容量半導体メモリ,半導体製造技術を用いた化学センサ,自動車向け半導体感性センサ,IoT無線センサによるモニタリング技術などの開発に従事.現在はCMOSアニーリング技術の研究を推進している.
採録決定:2025年2月5日
編集担当:烏谷 彰(富士通(株))