金融業界における量子コンピューティング活用に向けた取り組み
また,より近い将来を意図した取り組みとして,機械学習アルゴリズムを用いた金融不正検知への応用を試みた.量子コンピュータへのデータエンコードは,量子コンピュータで実社会問題に取り組む際の大きな課題である.たとえば機械学習を行う際は,量子コンピュータに大量の学習データを学習のたびにエンコードする必要があり,このデータエンコードがボトルネックになり得る.そこで,我々は,効率的に動作するデータエンコーダを開発した.このエンコーダを用いて実際に9量子ビットにデータをエンコードし,不正検知問題を実行することができた.
1.金融業界における量子コンピューティングへの期待
1.1 金融業務の現状
金融業界と数値計算は密接に結びついている.歴史的には,数理ファイナンスや統計学などの知見を用いて,リスクの定量化ができたことで,魅力的な商品開発やリスク管理に繋がり,業界が進歩してきた.また,近年の機械学習の発展により,金融計算分野だけでなく,多くの顧客サービスの改善がなされた.数値計算の精度が,価格競争力や顧客満足度,経営の健全性に影響を与える業界と言える.一方,数値計算モデルの複雑化や大量データの活用により,より多くの計算資源が求められており,効率的な数値計算技術の開発が続けられている.
1.2 量子コンピュータがもたらす可能性
量子コンピュータは,量子力学の原理に基づくコンピュータであり,量子コンピュータを用いた量子アルゴリズムを用いることで,金融業務で行われる数値計算をより効率的に実行できると期待される.そのため多くの金融機関が,量子アルゴリズムのキラーアプリケーション探索を行い,金融問題への適用を検討している.量子コンピュータの実機は発展途上にあり,2025年時点では,実社会の金融の数値計算を解決するのは困難であるが,トイ・プロブレム(小規模なサンプル問題)を用いた有用性の検証が行われてきた.この章では,具体例を紹介する.
1.2.1 デリバティブの価格決定
金融業界での主要なユースケースに,金融派生商品,いわゆるデリバティブ商品の価格計算問題がある.デリバティブ商品は数理ファイナンスによって大きく発展した商品であり,株や為替などといった原資産を確率微分方程式でモデル化し,その将来の確率的な変動を考慮して,商品の価格やリスク量を計算する.
原資産は常に市場環境で変動するため,デリバティブの価格もそれに応じて変動する.金融機関は,日次またはそれ以上の頻度でデリバティブの価格計算を行うことが一般的であり,計算の高速化に強いニーズがある.また,より精緻な価格計算が価格競争力につながることが期待できる.
従来コンピュータによる計算手法では,複数の解法が知られている.たとえば,確率微分方程式を偏微分方程式に読み替え,偏微分方程式を有限差分法などを用いて解く手法や,確率微分方程式を離散近似しモンテカルロ積分法で評価する手法が代表的である.
量子コンピュータの研究でも,複数の解法が研究されている.たとえば,量子コンピュータで積分計算を行う「量子数値積分アルゴリズム」が提案されている.この量子アルゴリズムは従来コンピュータのアルゴリズムに対して優位性が知られる例となっており,2章にて詳細を説明する.
研究の多くは,簡単に解けるトイ・プロブレムに量子アルゴリズムを適用したものであるが,実務でより興味のある複雑な商品への適用も研究例がある.一方,実務上は,複雑な商品こそ新技術によって計算を改善したいニーズがあるが,量子コンピュータでトイ・プロブレム以上の複雑な問題を取り扱うには,具体的な実装方法の検討など課題が残っている.
1.2.2 機械学習への応用
金融業界では,確率解析のモデル化とともに,統計によるモデル化も広く行われている.特に実際のデータに基づくリスク管理の分野において重要な技術であり,大規模データを用いた企業倒産予測やトレーディングポートフォリオの損失計算などに用いられてきた.近年,データの増加と機械学習の発展により大きく進歩を遂げた分野でもある.
金融業務への機械学習のユースケースは非常に多岐にわたる.たとえば,クレジットカードや住宅ローン貸出の審査は,大規模データと機械学習を活用した自動化・効率化が期待される分野であり,より早期かつ正確な審査が顧客サービスの向上につながる.また,経済をより正確に予測できるようになれば,金融機関の機動的な経営判断や,適切な資産分配やより健全な経営につながることが期待される.
量子コンピュータにおける機械学習は,従来コンピュータによる機械学習アルゴリズムにおける,サブルーチンとしての研究がなされてきたが,近年は量子回路そのものを機械学習の対象とする研究もある.
前者の例として,量子コンピュータの線形代数計算における優位性に起因するものが挙げられる.本方法では量子コンピュータの計算能力を活用した機械学習の高速化が期待される一方で,量子コンピュータへのデータエンコード(埋め込み)の問題などがあり,いくつかの克服すべき課題が存在する.
また後者の例として,回路学習を端緒に発展したものがある.本方法では,変分量子回路(パラメータ制御が可能な量子回路)と呼ばれる量子回路を用い,データに対して回路のパラメータを学習していく.本方法は従来コンピュータの機械学習の技術を取り入れ,多くの研究がなされた.特に量子回路をより浅くすることが可能であり,短期的な実機での応用が期待される一方,学習の難しさが課題とされる.金融分野における応用例としては,ボラティリティ予測やリスク管理などが研究対象となっている.
金融に関するデータは大量かつ複雑であるため,解釈可能で有用なデータを作成することが望ましい.このようなデータは特徴量と呼ばれ,その作成プロセスは特徴量の抽出と呼ばれる.たとえば,量子主成分分析では量子ビットの特性を活かした複雑な特徴量が得られる利点があるが,量子コンピュータにより出力されるデータから有用な情報を得ることが難しいという問題も存在する.
2.量子数値積分アルゴリズムによるデリバティブ価格評価
この章では,1.2.1項で触れた量子数値積分アルゴリズムについて説明し,その改良について議論する.初期の量子数値積分アルゴリズムは,量子ビット数やゲート数のコストが非常に高いという課題があった.また,現状の量子コンピュータはエラーが大きく,エラーを適切に考慮したアルゴリズムが必要となる.我々はこれらの問題を克服するために改良アルゴリズムを提案した.以下ではこれらのアルゴリズムについて説明し,数値実験によってその有効性を検証した結果を紹介する.
2.1 量子数値積分アルゴリズムとその改良
量子数値積分アルゴリズムは,量子状態の振幅に積分値を埋め込み,「振幅推定」というアルゴリズムでこの値を推定することで所望の積分値を求めるアルゴリズムである.このアルゴリズムは従来コンピュータによるモンテカルロ積分法に比べて2次的な優位性があることが理論的に証明されている[1].「2次的な優位性」とは,たとえば従来のコンピュータで100万回の処理が必要な場合に,量子コンピュータではわずか数千回の処理で同等の精度が得られるということを意味する.したがって,量子コンピュータ側の単位処理あたりの実行時間を十分に小さくできれば,大幅に計算時間を削減できる.
図1(左)に,2002年に提案された初期の振幅推定アルゴリズム[2]の量子回路を示す.図中の \( \mathcal{A} \) はターゲットの関数を評価して所望の積分値を量子状態の振幅に埋め込む操作であり,\( \mathcal{Q} \) はGrover演算子と呼ばれる操作である.1つの \( \mathcal{Q}\) には \( \mathcal{A} \) の操作が2回分含まれている.Grover演算子\( \mathcal{Q}\) を使わずに,\( \mathcal{A} \)(関数の評価)のみを実行して振幅を推定することも可能であり,この場合は従来のコンピュータのアルゴリズムと同様の性能(関数の評価回数 \( N\) に対して精度誤差 \( \varepsilon=\mathcal{O}(1/\sqrt N) \) )となる.\(\mathcal{Q}\) を実行することで,ある推定精度を達成するために必要な \( \mathcal{A}\) の実行回数を2次的に削減する(精度誤差 \( \varepsilon=\mathcal{O}(1/N)\) とする)ことができる.これが量子効果による優位性である.
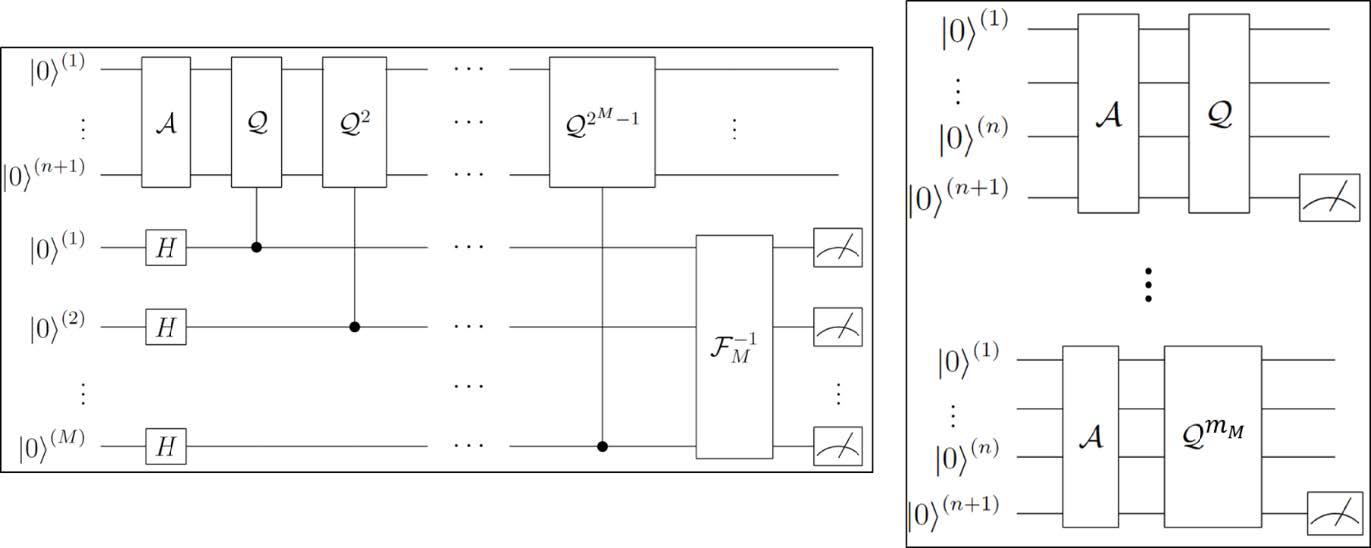
(右)提案アルゴリズム(MLAE)で実行する量子回路
このような優位性がある一方で,初期の振幅推定アルゴリズムには,逆量子フーリエ変換(図1(左)中の \( \mathcal{F}_M^{-1} \) )と呼ばれる多数の量子ゲート・量子ビットを必要とするコストの大きい処理が含まれているという課題があった.
この課題に対し,我々は逆量子フーリエ変換を必要としない振幅推定アルゴリズム(MLAE:Maximum likelihood amplitude estimation アルゴリズム)を提案した[3].MLAEアルゴリズムでは,量子コンピュータの出力を従来コンピュータで統計処理(最尤推定:Maximum likelihood estimation)し,振幅の推定値を得る.図1(右)がMLAEアルゴリズムの量子回路であり,逆量子フーリエ変換 \( \mathcal{F}_M^{-1} \) が含まれていないことが分かる.
図2に,MLAEアルゴリズムを用いてsin関数の積分という簡単な例を対象に,推定精度を数値的に評価した結果を示す.この結果から,関数の評価回数( \( \mathcal{A} \) の数)を100倍にすると,Grover演算子を用いない場合は約10倍の精度向上,MLAEアルゴリズムでは約100倍の精度向上が得られることが分かる.したがって,従来の振幅推定と同様に,MLAEアルゴリズムはGrover演算子を用いない場合に比べて2次的な優位性があることが確認された.
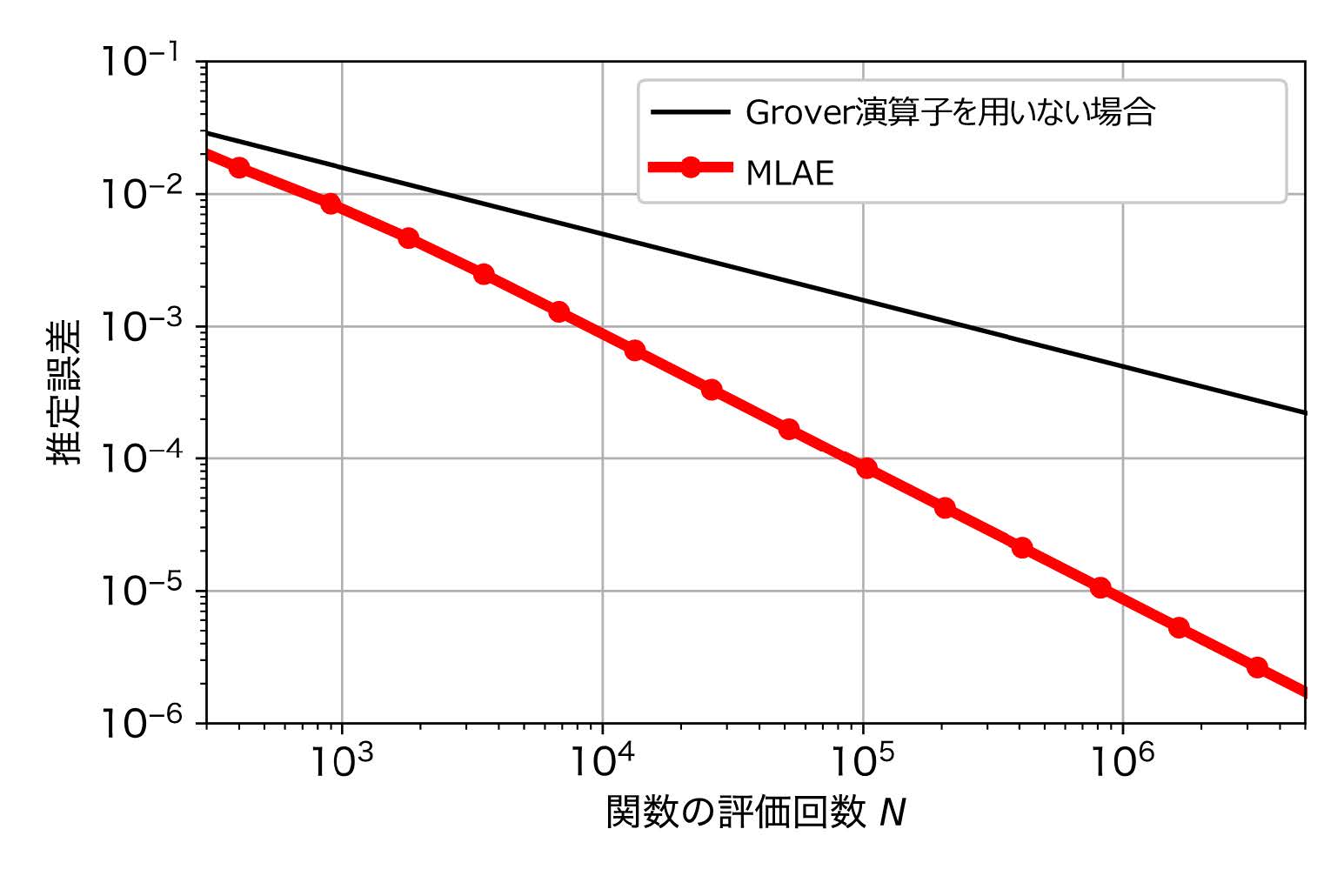
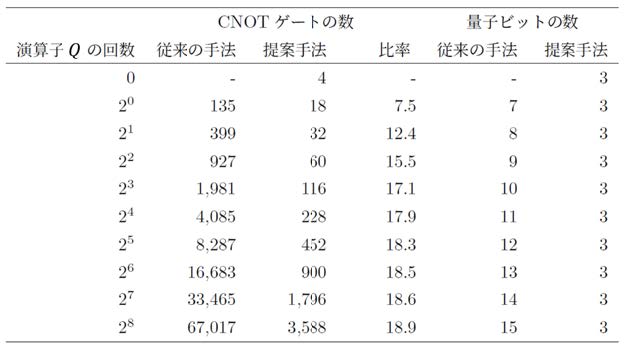
表1にMLAEアルゴリズムによるコスト(量子ビット数・ゲート数)の削減について検証した結果を示す.sin関数の積分を対象とした場合,MLAEアルゴリズムでは,従来の振幅推定アルゴリズムと比較して,量子ビット数を最大1/5,ゲート数は約1/20に削減できることが確認された.
2.2 量子コンピュータのエラーへの対応
次に,実際の量子コンピュータでMLAEアルゴリズムを実行するために行ったアルゴリズムの改良と,数値実験の結果について紹介する.
量子コンピュータは,外部ノイズの影響や制御の不具合により一定の確率で処理にエラーが発生する.現状の量子コンピュータはこのエラーを十分に訂正することができないため,エラーの影響を考慮したアルゴリズムが重要となる.MLAEアルゴリズムについても,量子コンピュータ実機で実行するために,エラーを考慮したアルゴリズムに改良した[4].具体的には,エラーの“強度”を未知パラメータとし,従来コンピュータによる統計処理(最尤推定)の際に振幅とエラー強度の2値を推定するようにした.
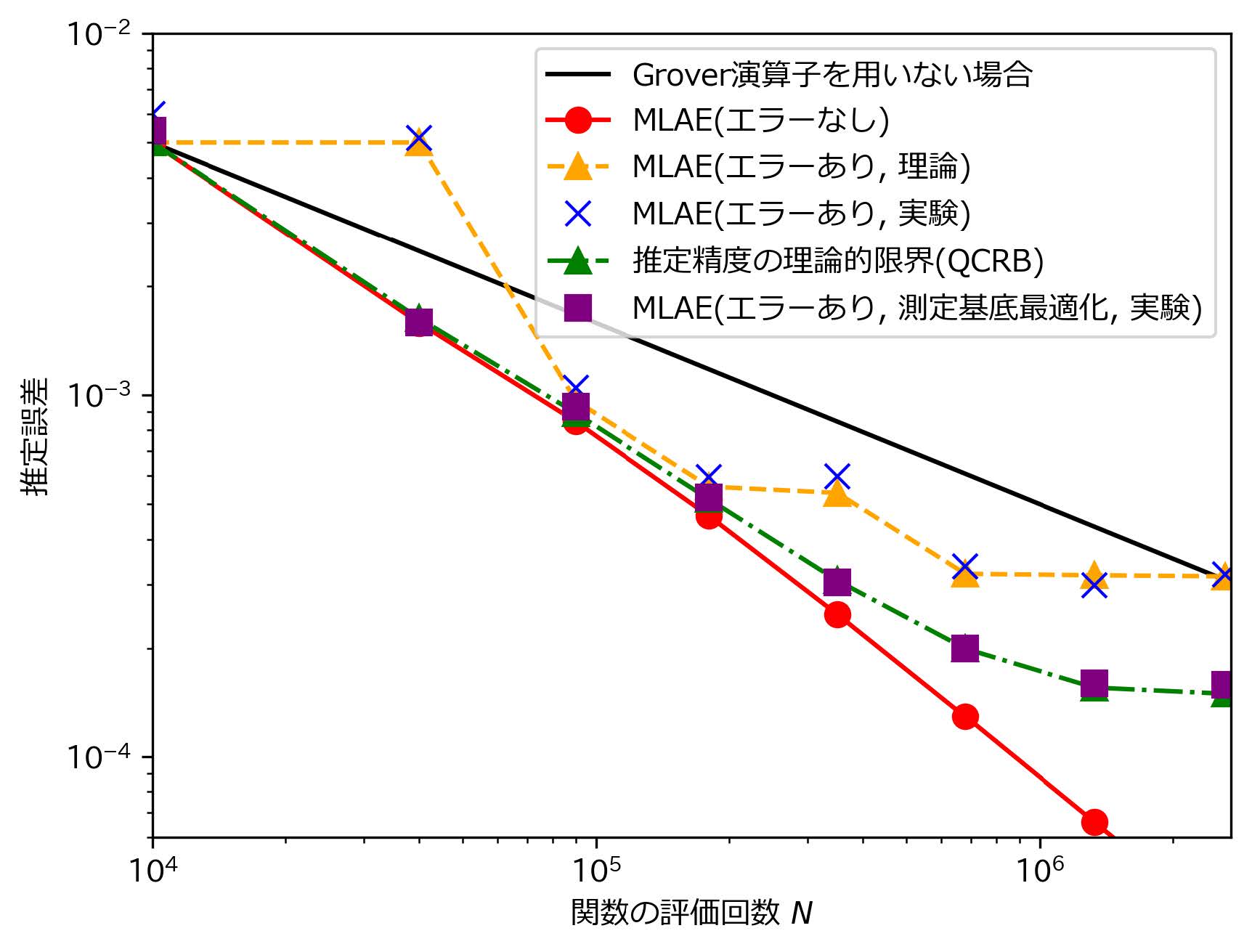
このアルゴリズムについて,上記と同様のsin関数の積分を対象に量子コンピュータ実機(IBM Quantum [5] “ibmq_valencia”,実験日2020年6月☆1)を使って数値実験を行った結果を図3に示す.実験で得られた推定誤差が従来コンピュータのアルゴリズムによる下限を超え,量子アルゴリズムで理論的に予測される誤差の下限に近い値を示したことから,提案手法は量子コンピュータの実機で発生するノイズに適切に対処し,正確に振幅推定を行えていることが確認された.
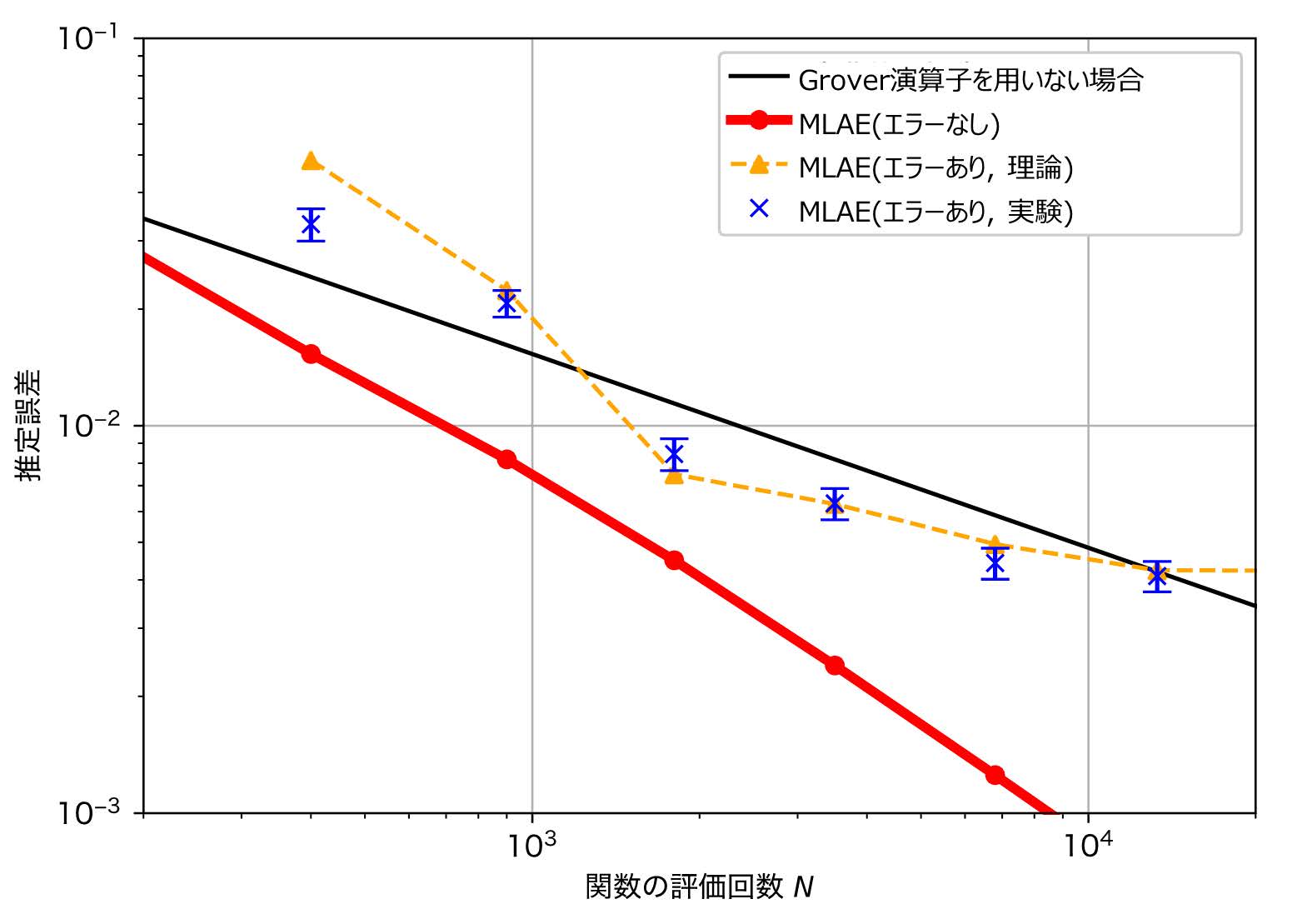
さらに,上記のアルゴリズムを発展させることで,推定精度を限界まで高める改良を行った.量子コンピュータの処理にエラーがある場合には,振幅推定の精度は量子回路の測定方法(測定基底)に依存することが知られている[6,7].そこで,MLAEアルゴリズムをさらに改良し,測定を最適化することで,エラー存在下における推定精度の理論的限界(QCRB:Quantum Cramér–Rao bound)を達成するアルゴリズムを提案した[8].このアルゴリズムでは,変分量子回路を使用し,測定を最適化するようにパラメータの調整を行う.パラメータ調整と振幅推定は同時に実行することができ,「ラフな振幅推定 と パラメータ調整」→「最適化された測定での振幅推定」という2段階の推定手順を経ることで,QCRBを達成することが可能となる.
このアルゴリズムについて, sin関数の積分を対象にシミュレータを使って数値実験を行った結果を図4に示す.実験結果から,提案したアルゴリズムにより,変分量子回路の最適化が上手くいく場合には,測定基底を最適化しない場合に比べて推定精度が改善され,QCRBを達成できることが確認された.
2.3 まとめと課題
本章では,リスク評価やデリバティブ価格評価等に利用できる振幅推定アルゴリズムについて,その改良とデモンストレーションの結果を紹介した.なお,検証ではsin関数という比較的容易に量子回路として実装できるものを対象としていた.3章でも議論するように,実問題で求めたい積分値を量子回路に“埋め込む”のは一般に大きなコストがかかる.そのため,効率的な埋め込み手法を開発し,実用的な問題に対して量子数値積分アルゴリズムを適用していくことが今後の重要な課題となる.
3.量子機械学習による金融不正検知
3.1 金融における機械学習による判別問題
近年,機械学習は,他業界と同様,金融業界においても,融資分野,資産運用業務,市場分析業務,リスク管理業務などで活用され始めており,その活用範囲は急速な広がりを見せつつある.その目的や手法は多岐にわたるが,金融犯罪の検知への応用も代表的なユースケースの一例である.
特に,クレジットカードの不正利用は,顧客保護,金融犯罪防止,企業財務への悪影響回避の観点から,社会問題となっている.金融機関にとっても深刻な問題であり,クレジットカードの不正利用による損失は,2030年までに世界全体で493億ドルに達すると予想されている.デジタル犯罪やオンライン詐欺が増加する中,金融機関にとって,高度な技術と強力なセキュリティ対策によってクレジットカード詐欺を防止することは,これまで以上に重要である.カード不正は,カード会員の属性や過去の取引履歴,商品の配送先情報などをもとに検知することができるが,手口が巧妙化している不正利用被害に対してさらなる検知精度の向上を目指す必要がある.また,近年,クレジットカードの取引データから抽出した特徴量を用いた機械学習による不正検知の試みも注目されているが,安定した性能に収束するまでの計算時間の増加や過学習といったデメリットがある.量子機械学習はこれらの課題を解決する可能性を秘めている.
3.2 量子機械学習の抱える課題,データ埋め込みの重要性
量子コンピュータは量子干渉を使って指数関数的に大きな量のデータを表現しつつ演算できる可能性があり,機械学習においても応用が研究されている.一方,これらの応用には,使用できる量子ビット数の制限や,実行できる演算数の制限,ノイズによるエラーなど解決すべき課題が多くある.このような制限の中,なるべく少ない演算で実行できる分類器の研究が進んでおり,スワップテスト分類器(SWAP-Test Classifier),アダマールテスト分類器(HTC:Hadamard Test分類器),コンパクトアダマール分類器(CHC:Compact Hadamard分類器)など,浅い量子回路上に機械学習アルゴリズムを実装する試みがなされている.これらの分類器の根底にある考えは,指数関数的に大きなデータの内積を複雑なサブルーチンを使わずに測定によって直接計算するというものである.しかし,これらの分類器は,訓練データとテストデータが量子状態の振幅(量子振幅)にエンコードされていること,すなわち振幅エンコーディングを前提としていることに注意が必要である.
一般に,量子コンピュータへのでデータエンコーディング(埋め込み)は多くの演算数を必要とし,たとえば振幅エンコーディングを実現するためのゲート数は量子ビット数に応じて指数関数的に増加する.これでは,いかに量子機械学習アルゴリズムが効率的にできたとしても,データエンコーディングの困難性により,全体の性能を損なってしまう.この問題を解決するために,先行研究[9]においては変分量子回路(パラメータ付き量子回路)を用いて,\( N \) 量子ビットのデータエンコーディングを \( \mathcal{O}(\text{poly}(N)) \) ゲートで生成する近似的振幅エンコーディング(AAE:Approximate Amplitude Encoding)と呼ばれるアルゴリズムが提案されており,少ない演算数で近似的な実数値のデータを埋め込むことができる.一方,量子の振幅は一般に複素数であるが,AAEでは実数値のみに有効であり複素数値のデータを埋め込むことはできない.この制限がAAEの適用範囲を狭めてしまい,たとえば,AAEで埋め込んだデータは前述のCHCには適用できない.CHC以外にも,効率的な複素数値データのエンコーディング(埋め込み)が必要な例は多く知られており,エンコーディング方法の改良には強いニーズがある.
3.3 データ埋め込みの改良
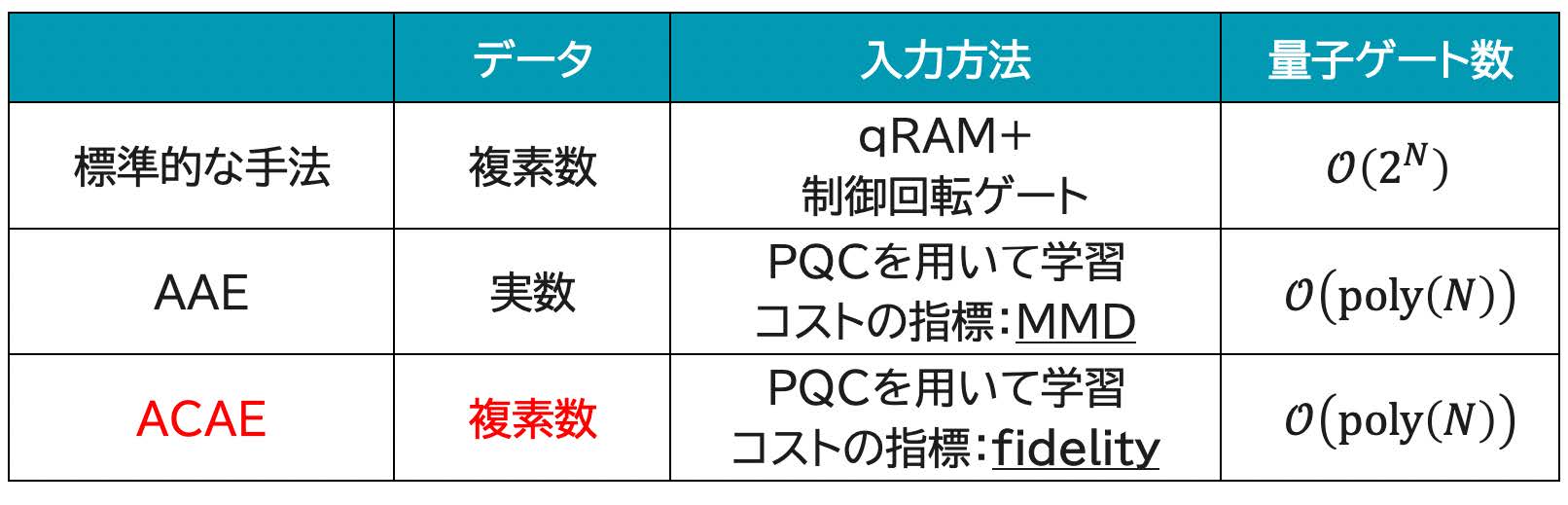
我々はAAE[9]を拡張し,複素数値のデータを浅い量子回路に近似的にエンコードする(埋め込む)手法ACAE[10]を開発した.既存の手法との比較を表2に示す.ACAEはAAEと同様に \( \mathcal{O}(poly(N)) \) ゲートの少ない演算数で任意の複素数値データを振幅に埋め込むことができる.この埋め込みにおいて重要なアイデアは,コスト関数をAAEで使用される最大平均不一致(MMD:Maximum Mean Discrepancy)から,2つの量子状態の忠実度(fidelity)に変更することである.fidelityはMMDベースのコスト関数とは異なり,2つの量子状態間の複素振幅の差を捉えることができる.特筆すべき点は,限られた数の測定で量子状態を推定することができる方法(classical shadow)を用いて,fidelityやその勾配を効率的に推定する点にある.
3.4 数値実験結果
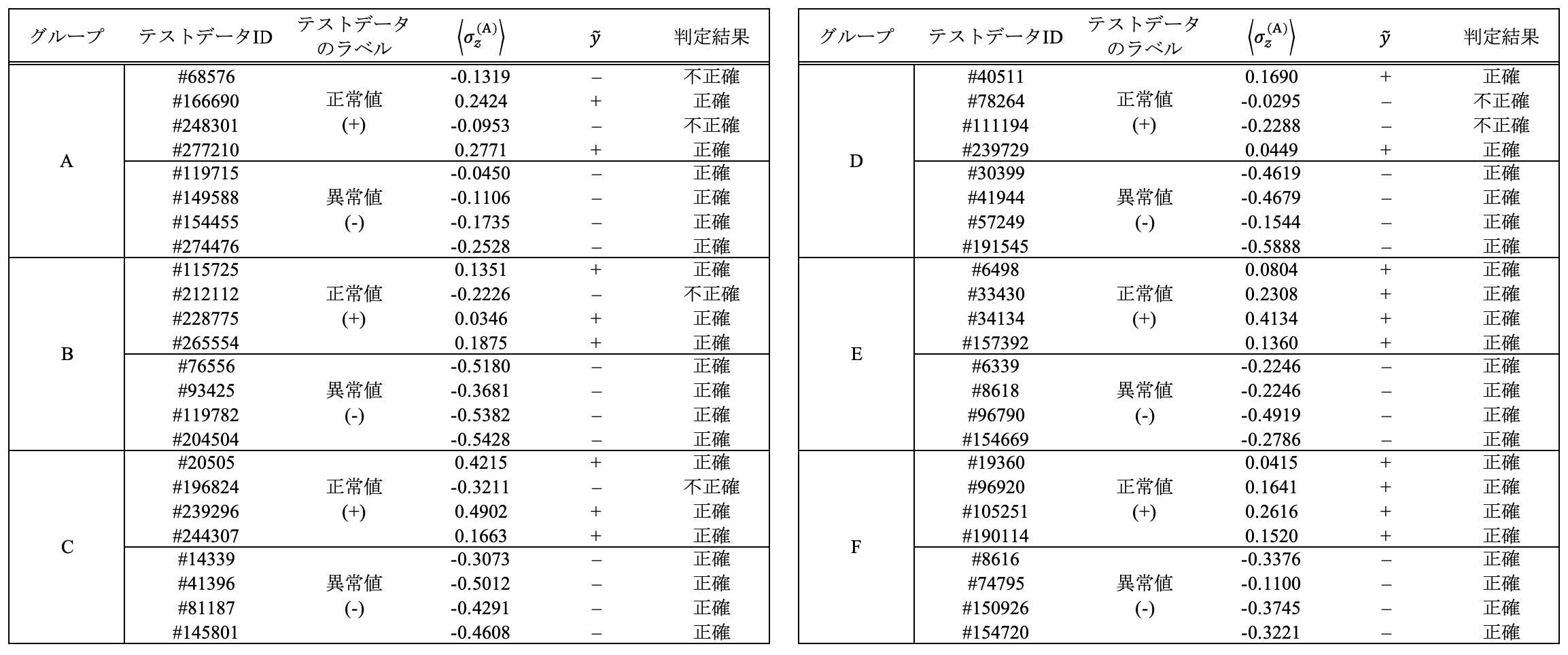
本節では,ACAEとCHCからなる我々のアルゴリズムの性能を示すために,Kaggleで提供されているクレジットカード詐欺データセット[11]を用いた詐欺検出問題への応用の実験結果を紹介する.検証に用いたデータは,2013年9月に欧州で行われたクレジットカード取引情報(総取引件数284,807件,うち不正取引件数492件)が含まれている.すべての取引データをエンコードするのは現状は困難であるため,概念実証テストを実施した.本実験では,前述のKaggleのデータセット28万件のうち数十件を抽出し,ACAEによって近似値を生成し,前述のCHCに埋め込むことで2値分類問題(クレジットカードの正常取引と不正取引の判定)を行った.データセットから無作為に選んだ正常な取引データと不正な取引データを学習データとして用い,与えられたテストデータが正常か不正かを判定する分類テストを8件(正常な取引データ:4件,不正な取引データ:4件)のテストデータに対して6回実施した(表3).その結果,48個のテストデータのうち42個が正しく分類されていることを確認した.残りの6つのテストデータは誤って分類されたが,この誤分類はエンコーディングの誤りではなく,データセットの本質的な特性や学習データの不足に起因する可能性があると考えられる.
3.5 まとめと課題
本章では,機械学習で本質的な課題となる量子コンピュータへのデータエンコーディングにかかわる問題点に触れ,新しいデータエンコーディング手法として,複素数値のデータを浅い変分量子回路を用いて効率的にエンコードできるACAEを紹介した.また,ACAEで準備した量子データと2値分類問題の分類器であるCHCを組み合わせ,End to Endでクレジットカード不正検知という,実問題へ量子機械学習を適用した.今回の実験では問題のサイズが限定的であったが,ACAEをさらに大きなデータへ適用するには課題もある.本実験で,高いデータエンコード精度を維持すると,量子ビット数に対して量子回路の深さが超線形的に増加する,量子回路の深さとデータの精度とのトレードオフが見られた.一方,データ精度を多少犠牲にしたとしても,一定程度の分類精度を示すことも確認できており,求められる分類精度に応じて適切なトレードオフを選択していくことが重要になる.
4.結論と展望
本稿では,量子コンピュータを金融分野で活用するための具体例を紹介した.現状では,実社会の課題を解決するまでには至っていないが,昨今のハードウェア・アルゴリズムの技術革新は急速であり,近い将来に何らかの形で利用可能になると期待される.
量子アルゴリズムは,従来コンピュータのアルゴリズムとは相違点も多く,知見の醸成には時間がかかることから,長期スパンでの研究活動の継続が重要となる.
参考文献
- 1)Montanaro, A. : Quantum Speedup of Monte Carlo Methods, Proc. Royal Soc. A 471, 20150301 (2015).
- 2)Brassard, G., Høyer, P., Mosca, M. and Tapp, A. : Quantum Amplitude Amplification and Estimation, Contemporary Mathematics Series Millenium 305, 53–74 (2002).
- 3)Suzuki, Y., Uno, S., Raymond, R., Tanaka, T., Onodera, T. and Yamamoto, N. : Amplitude Estimation Without Phase Estimation, Quantum Information Processing, 19, 1-17 (2019).
- 4)Tanaka, T., Suzuki, Y., Uno, S., Raymond, R., Onodera, T. and Yamamoto, N. : Amplitude Estimation via Maximum Likelihood on Noisy Quantum Computer, Quantum Information Processing, 20, 1-29 (2021).
- 5)IBM Quantum : https://quantum.ibm.com/ (2021).
- 6)Uno, S., Suzuki, Y., Hisanaga, K., Raymond, R., Tanaka, T., Onodera, T. and Yamamoto, N. : Modified Grover Operator for Quantum Amplitude Estimation, New Journal of Physics, 23(8), 083031 (2021).
- 7)Wada, K., Fukuchi, K. and Yamamoto, N. : Quantum-Enhanced Mean Value Estimation via Adaptive Measurement, Quantum, 8, 1463 (2024).
- 8)Oshio, K., Suzuki, Y., Wada, K., Hisanaga, K., Uno, S. and Yamamoto, N. : Adaptive Measurement Strategy for Noisy Quantum Amplitude Estimation With Variational Quantum Circuits, arXiv preprint arXiv:2405.15174.
- 9)Nakaji, K., Uno, S., Suzuki, Y., Raymond, R., Onodera, T., Tanaka, T., Tezuka, H., Mitsuda, N. and Yamamoto, N. : Approximate Amplitude Encoding in Shallow Parameterized Quantum Circuits and Its Application to Financial Market Indicators, Phys. Rev. Res. 4 (2022).
- 10)Mitsuda, N., Ichimura, T., Nakaji, K., Suzuki, Y., Tanaka, T., Raymond, R., Tezuka, H., Onodera, T. and Yamamoto, N. : Approximate Complex Amplitude Encoding Algorithm and Its Application to Data Classification Problems, Phys. Rev. A (Coll. Park.) 109 (2024).
- 11)Credit card fraud detection : https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
脚注
- ☆1 本稿で紹介した研究は,IBM Quantum の諸サービスを利用したものである.本稿の見解は,筆者らのものであり,IBM または IBM Quantum の公式な方針または立場を反映するものではないことに注意されたい.

加藤準平
jiyunpei_katou@mufg.jp
2015年三菱UFJフィナンシャル・グループ,三菱UFJ銀行に入行し,2023年まで信用リスク計測業務に従事.2023年より慶應義塾大学量子コンピューティングセンター共同研究員を兼任し,量子コンピューティングを担当.

大塩耕平
kohei.oshio@mizuho-rt.co.jp
2020年みずほリサーチ&テクノロジーズに入社し,物性物理・化学分野における解析・開発・調査業務に従事.2022年より慶應義塾大学量子コンピューティングセンター共同研究員を兼任し,量子アルゴリズムの研究に取り組む.

市村達大
Ichimura_Tatsuhiro@smtb.jp
2019年三井住友信託銀行に中途入社し,2023年までオルタナティブ投資・運用業務に従事.2023年より慶應義塾大学量子コンピューティングセンター共同研究員に出向し,量子コンピューティングの研究開発を担当.

鈴木洋一(正会員)
suzuki.yohichi@aist.go.jp
2024年産業技術総合研究所,量子・AI融合技術ビジネス開発グローバル研究センターへ入所.量子アルゴリズムの研究,ユースケースの探索に取り組む.

森 義治(正会員)
ymori@keio.jp
2023年慶應義塾大学量子コンピューティングセンターに着任.量子コンピュータを活用した物理・化学および金融の分野における実用的量子アルゴリズムの研究に取り組む.
採録決定:2025年2月17日
編集担当:木村直紀(ヤフー(株))