1．量子化学計算と量子コンピュータ

1.1　化学におけるシミュレーションと量子化学

現在の製造業においては，分野を問わずコンピュータシミュレーションは重要な役割を占めている．たとえば化学企業における活用を例にとるとスケールの小さいほうから順に

• （1）材料中の電子のふるまいを理解するための量子力学シミュレーション
• （2）原子スケールでの原子・分子の挙動理解するための分子動力学シミュレーション
• （3）より大きなスケールにおける連続体・流体シミュレーション

という階層構造がある．これらの過程は異なった空間・時間的なスケールを持ち，たとえば原子電子の挙動のシミュレーションは1nm（ナノメートル）以下の大きさを扱うが，（３）のシミュレーションはm（メートル）のオーダーを扱うことになり得る．特に現代の製造業は，製品の微細化・高性能化を要求されることが多く，電子のふるまいを制御することが製品製造の鍵となってきている．

本稿で注目するのは（1）の電子シミュレーションであり，一般には「量子化学計算」，もしくはもっと一般的には「第一原理電子状態計算」と呼ばれるものである（後者は原子・分子だけでなく，固体結晶などのシミュレーションも含まれるニュアンスの違いがある）．物質のさまざまな性質（たとえば化学結合・反応性・電気伝導性・磁性など）の大部分を決定するのはその中の電子のふるまいであり，シュレーディンガー方程式という量子力学の基礎方程式を解くことでそれらの特性を実験データにまったく頼ることなく予言・再現することができる（図1）．ここで図1に現れるシュレーディンガー方程式について少々解説しておくと，ギリシャ文字Ψ（プサイと読む）が電子の波動関数と呼ばれるもので，物質中の電子の確率分布と関連する関数である．$H$はハミルトニアンと呼ばれ，量子力学においてエネルギーを与える「演算子」であり，電子の運動エネルギー，電子と原子核の相互作用エネルギーなどから構成される．$E$は物質のエネルギーを表す．図1のシュレーディンガー方程式を解くということは，電子の波動関数Ψとエネルギー$E$を同時に求めることを意味する．シュレーディンガー方程式を満たすΨと$E$の組は1つだけではないが，その中でエネルギーが最も低い状態を基底状態（そのエネルギーを基底エネルギー），それ以外のエネルギーが高い状態を励起状態と呼ぶ．エネルギーが分かると何がうれしいのか？ということであるが，たとえばある分子を構成するの原子の配置を変化させて基底エネルギーを逐次計算したとき，エネルギーが最も小さくなる原子配置がその分子の最安定構造である．また，電子の波動関数が得られれば，電子の空間的な確率分布を見ることで，物質の化学結合の性質や反応性に関する知見などを得ることができる．

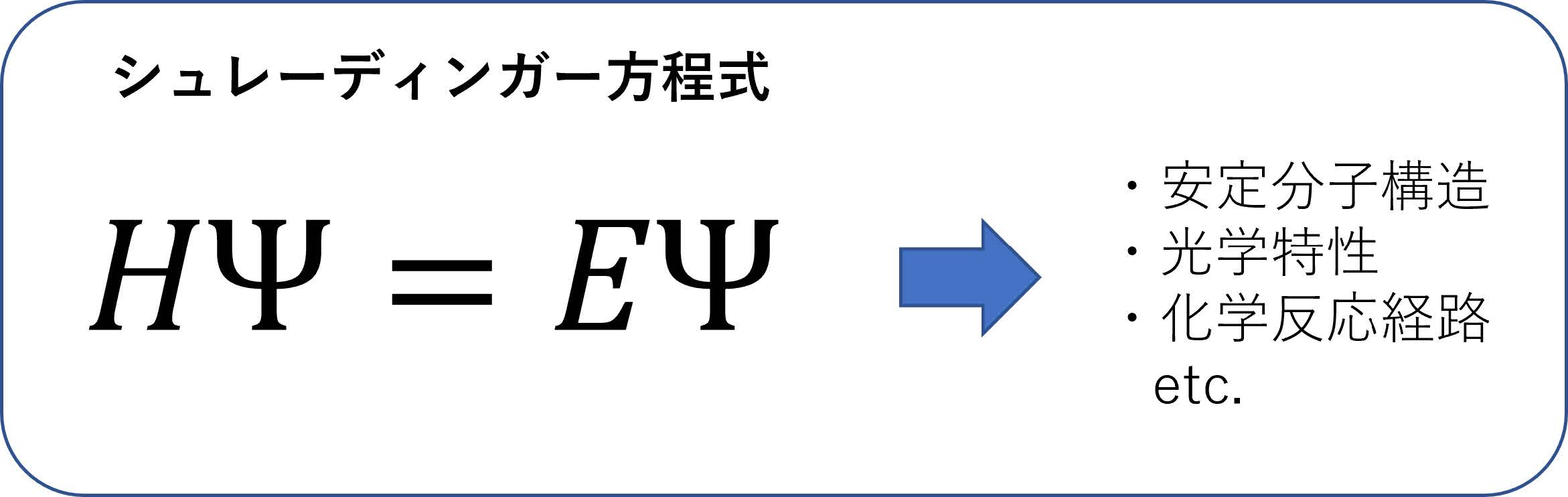
現在では，計算機および計算アルゴリズムの発展に伴い，分子や固体結晶の多くの性質をきわめて高精度でシミュレーションすることができ，量子化学はアカデミックな研究だけでなく，我々のような化学メーカーにおいても欠かすことができないものとなっている．

1.2　量子化学の難しさ

大成功を収めてきたといってもよい量子化学計算であるが，その適用には限界がある．その難しさの説明には，量子力学の基礎を説明する必要があるが，詳細は専門書を参考にしていただくとして概要だけを述べる．以下では説明を簡単にするために厳密さを欠いているところもあるが容赦されたい．量子力学においては，電子は分子の種類・構造によって定まる「分子軌道」をひとつずつ占有していくことが知られており（図2），シュレーディンガー方程式を厳密に解いて電子の波動関数Ψを求めるには，図2のように電子が分子軌道を占有するすべての組合せを考慮する必要がある．たとえば分子軌道が$N$個，電子が$M$個の場合（図2は$N=4$，$M=2$の場合），高校数学の組合せを使うと考慮すべき組合せの総数は $N!(N-M)!/M!$ のように指数関数的に増加し $(N!=N\times \; <!--\; multiplication\; sign\; -->(N-1)\times \; <!--\; multiplication\; sign\; -->\dots \; <!--\; horizontal\; ellipsis\; -->\times \; <!--\; multiplication\; sign\; -->2\times \; <!--\; multiplication\; sign\; -->1)$ ，分子のサイズが大きくなると手におえなくなる（表1参照）．もちろん現在使われている通常の計算アルゴリズムではすべての組合せをあらわに考えることはせず，たとえば分子の基底状態であれば図2の一番最初の項で表される1つの配置のみを考える，など計算を簡略化するための近似的な方法が用いられる．しかしこのような近似法はあくまで近似であり，厳密な答えをあたえるものではない．特に問題となるのは物質の光学特性などに関連する励起状態の性質であり，その波動関数を精度よく計算するには複数の電子配置をあらわに考える必要がある．励起状態の精密計算は材料化学のみならず，量子力学全体においても本質的な問題である．

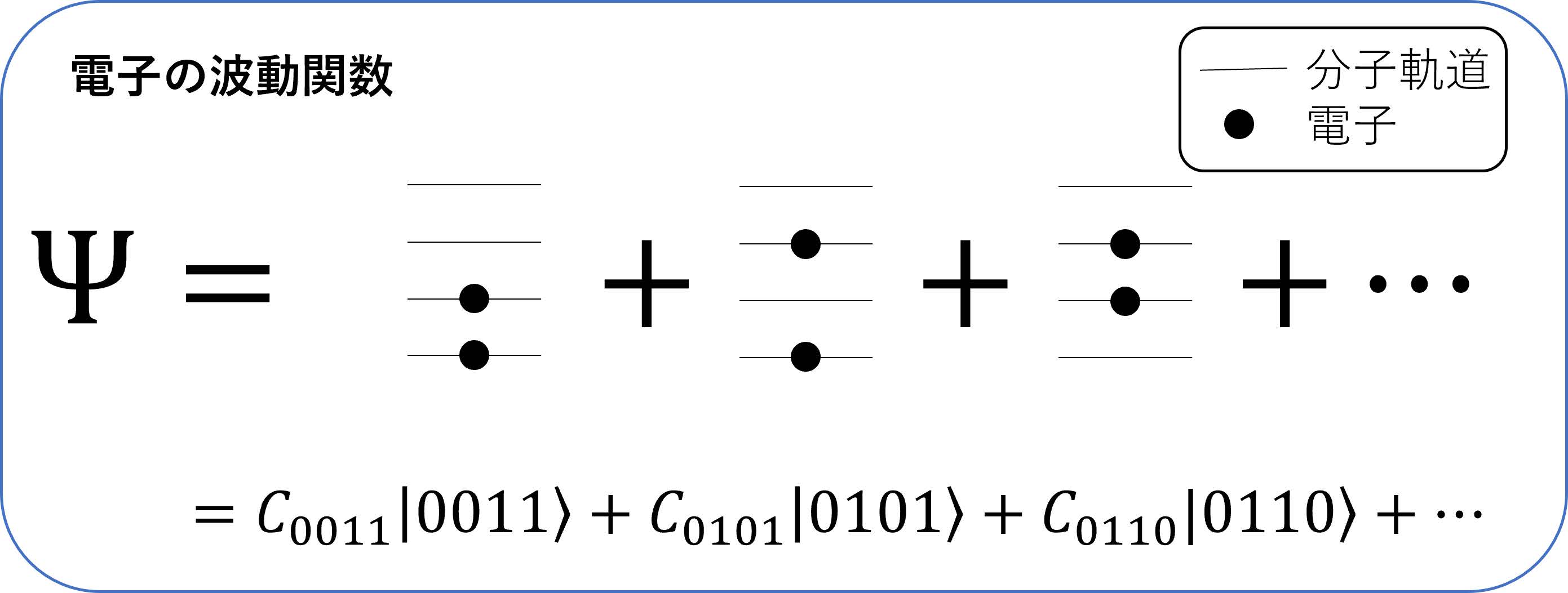
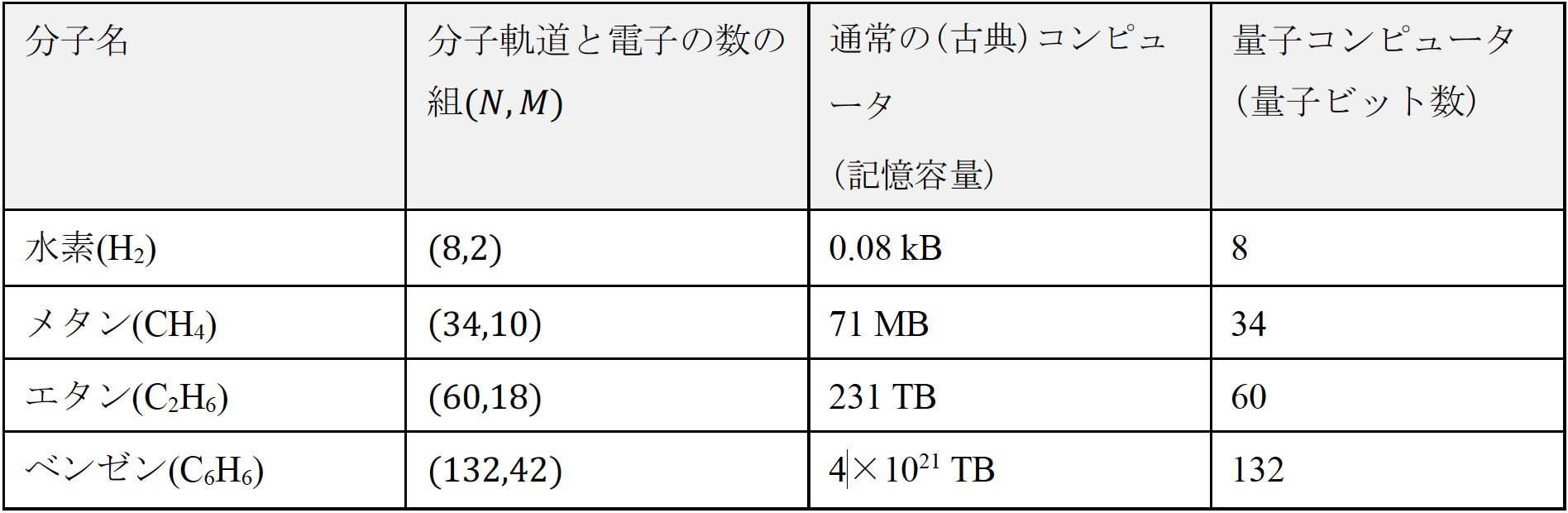
1.3　なぜ量子化学において量子コンピュータが注目されているか

そこで注目されているのが，2018年ごろから世間を騒がせるようになった量子コンピュータである．量子コンピュータが何か，またどのような原理で構築されるかということについては近年多くの解説書が出版されているので詳細については控えるが，恐らく一番のポイントとなるのは

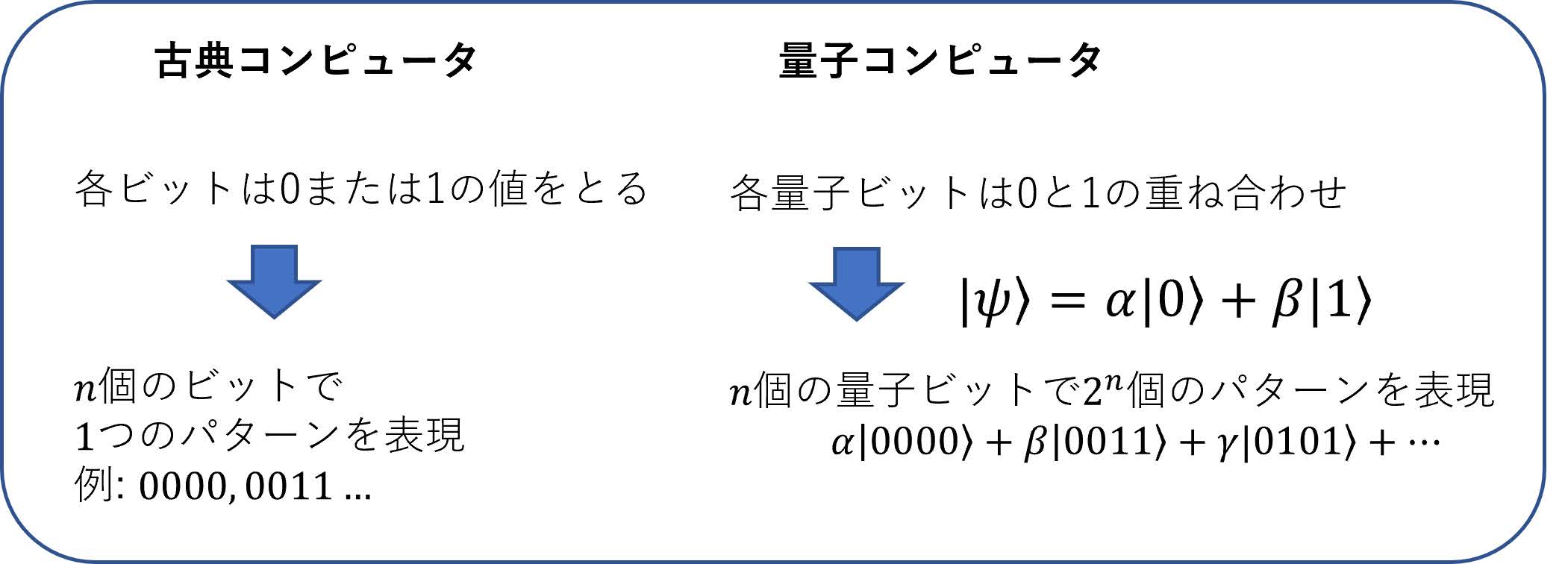
「通常のコンピュータ（量子コンピュータに対して，従来のコンピュータという意味で「古典」コンピュータと呼ばれる）における状態をあらわすビットは0か1のどちらかの状態をとるのに対し，量子コンピュータで対応するビット（量子ビットまたはキュービット（qubit）と呼ばれる）は0と1の2つの状態の重ね合わせで表される」

ということであろう（図3）．この「状態の重ね合わせ」というのは我々の日常生活においてはなじみがない不思議な概念であるが（興味のある方は文献[1]等を参照），この重ね合わせの性質は量子コンピュータの最大の特徴の1つである．ここで$\mathrm{\alpha \; <!--\; greek\; small\; letter\; alpha\; -->}|0⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->+\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}|1⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$という記法は0の状態（$|0⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$）と1の状態（$|1⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$）の重ね合わせ（数学的に言うと線形結合）を表す．$\mathrm{\alpha \; <!--\; greek\; small\; letter\; alpha\; -->},\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}$がその展開係数（または確率振幅）と呼ばれるもので，それぞれを2乗した${\mathrm{\alpha \; <!--\; greek\; small\; letter\; alpha\; -->}}^2,{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}^2$がそれぞれ量子ビットが0の状態，1の状態である確率を表す．たとえば$1/\sqrt{2}|0⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->+1/\sqrt{2}|1⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$という状態は，0の状態と1の状態がちょうど確率1/2ずつ混ざり合った状態であり，この状態を測定すると0のビットまたは1のビットが50%ずつの確率で得られる．なぜこの重ね合わせの原理が重要かというと，1つの量子ビットが同時に表現できるのは0と1のわずか2つであるが，量子ビットを$n$個並べると，表現できるビット列（0と1の並び）は$2\times \; <!--\; multiplication\; sign\; -->n$個でなく$2^n$個と指数関数的に増大していくことがポイントである（図3）．この性質は，量子ビットは古典コンピュータにおけるビットに比べて圧倒的な「表現能力」を持つということを示しており，うまく利用することで古典コンピュータに比べてある種の問題が指数関数的に高速に解ける，というのが量子コンピュータのおおざっぱな概念である．特に量子化学においては，図2の下部の式で示したように，ビットの数を分子軌道の数とし，0をその対応する分子軌道を電子が占有していない状態，1を電子が占有している状態という「約束事」で表すと，波動関数をビット列の重ね合わせで表すことができる．表1の右の列に示したように，量子ビットの性質を使うことで，電子の波動関数を古典コンピュータに比べて圧倒的に効率よく表現できるのである．

1.4　量子回路と量子化学計算

以降の説明と読者の便宜のため，図4に量子コンピュータにおける計算の「設計図」である量子回路とよばれるものの例を示す．IBM社のQiskit，Google社のCirqなど，量子回路のシミュレーション（古典コンピュータ上で量子回路のふるまいを模擬すること．そのために使うプログラムをシミュレータと呼ぶ）のためのライブラリがいくつか公開されており，簡単に利用することができる．またこれらのライブラリを通じてインターネットを経由し，公開されている量子コンピュータ実機での計算を行うことも可能である．

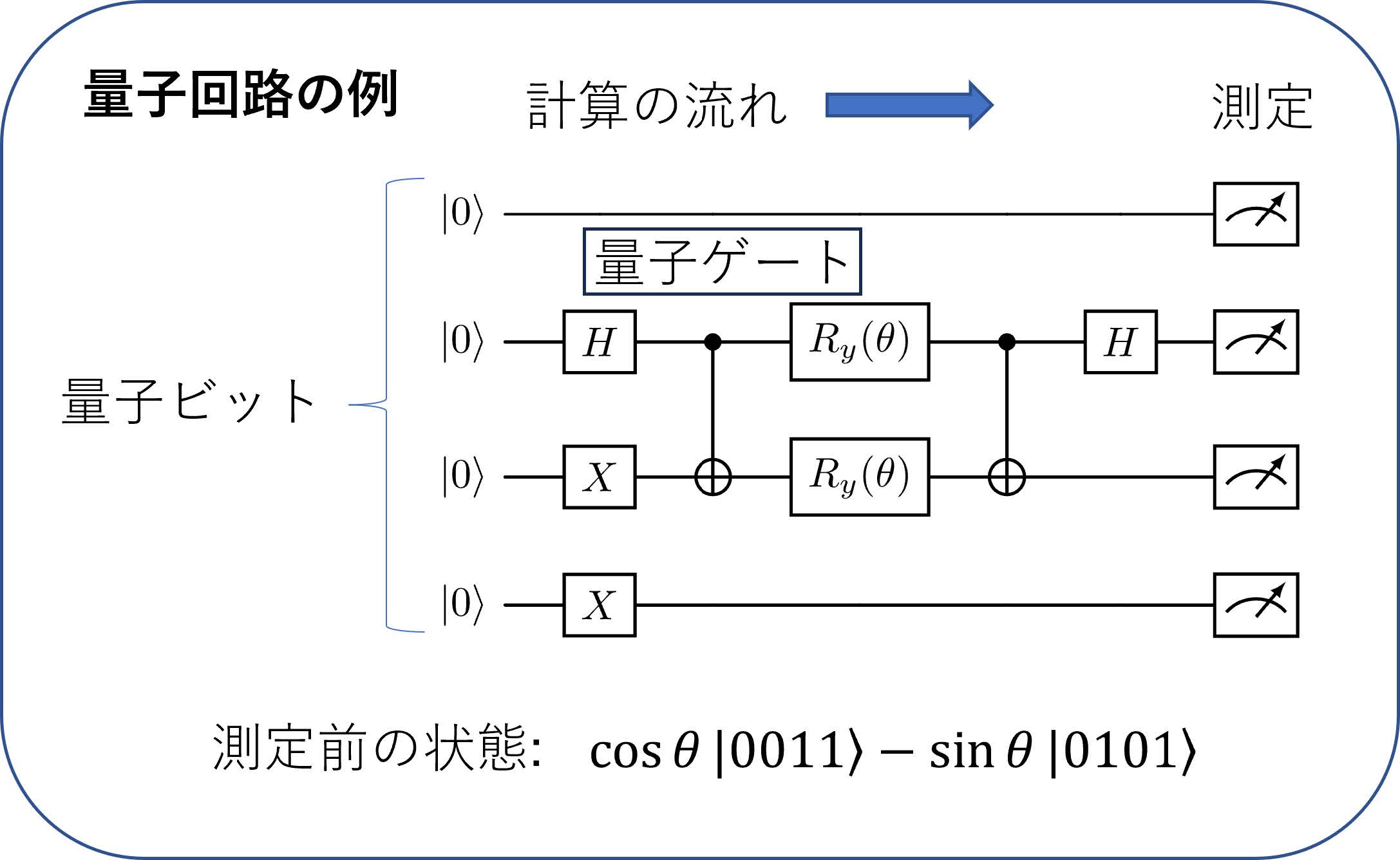
図4で縦に並んだものが各量子ビットを表し（この例は4量子ビット），各量子ビットは0の状態（$|0⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$）に初期化される．その後，各量子ビットに左から右の順にHやXなどの四角で囲われた「量子ゲート」と呼ばれる量子ビットの状態を操作する演算が作用されていく．図の中で2つの量子ビットに縦にまたがる演算子はCNOT演算子と呼ばれ，2つの量子ビットの状態に関連を持たせる（量子コンピュータの文脈では絡み合いをつくるという意味の「エンタングルさせる」などという言葉が使われる）重要な演算子である．これらの量子ゲートをうまく並べていくことで，所望の量子状態の重ね合わせを作成し，回路の最後（一番右）で状態を測定することで結果を得ることができる．この回路中の$Ry\left(\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}\right)$ゲートのように，量子ゲートにはユーザーが調整可能なパラメータ（この場合上から2番目と3番目の量子ビットの状態を変化させる角度$\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}$）を含めることができる．たとえば図4の量子回路では測定前の量子状態は$\cos \mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}|0011⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->-\sin \mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}|0101⟩\; <!--\; mathematical\; right\; angle\; bracket\; -->$となり，展開係数（確率振幅）がパラメータ$\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}$を含んだ形で表され，この状態の測定結果は「0011」と「0101」というビット列がそれぞれ${\cos }^2\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}$および${\sin }^2\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}$という確率で得られる．この量子回路で作られる状態と，図2の下部に表される電子の波動関数のビット表現の類似性に注目すると，量子ゲート（とその中に含まれるパラメータ）をうまく組み合わせることで，ビット列の組合せで表された電子の波動関数が厳密なものに近づくようにする，というのが量子コンピュータで量子化学計算を行う1つの方法である．

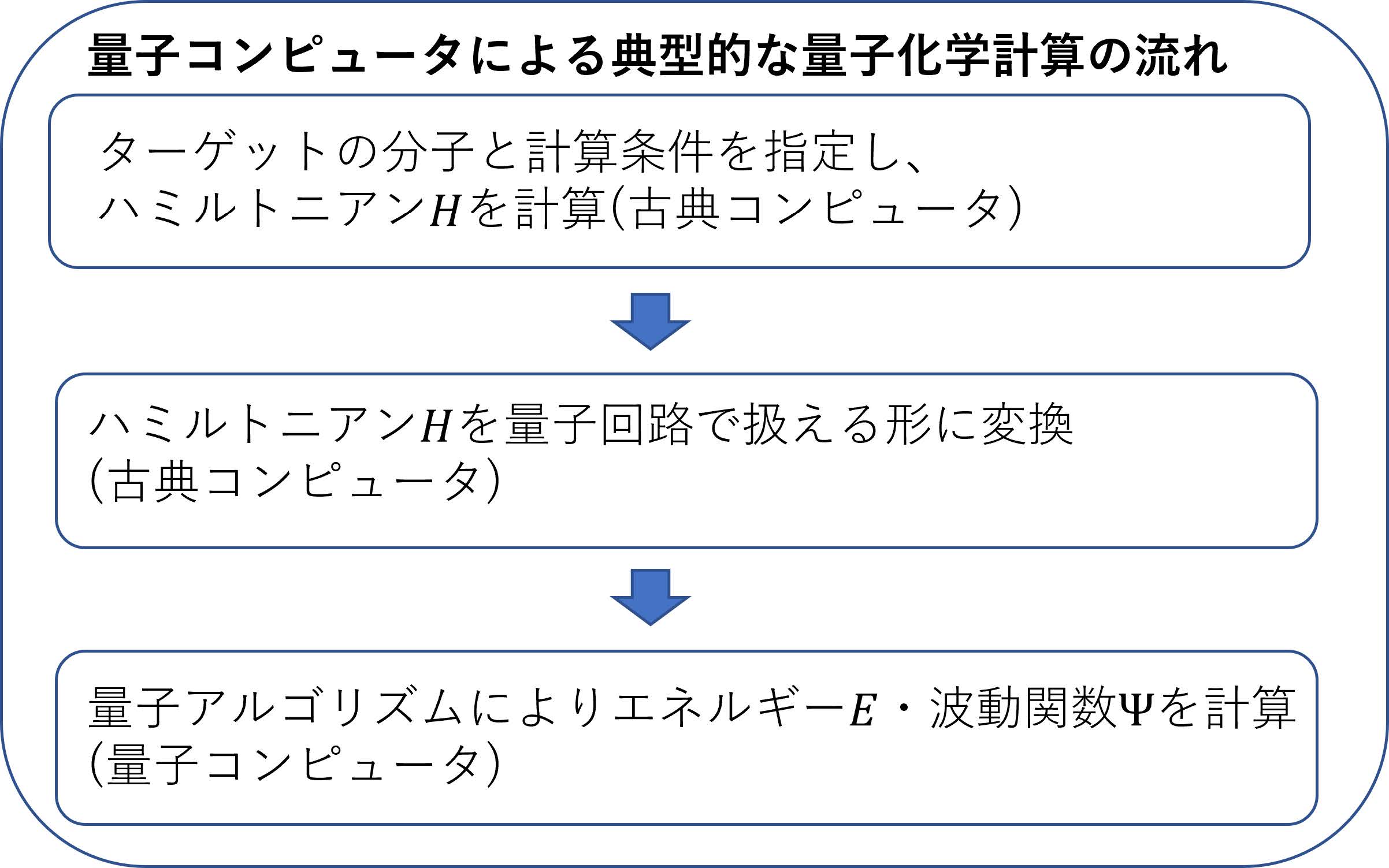
やや技術的な話になるが，興味のある読者のために，図5に量子コンピュータ（またはシミュレータ）で実際に量子化学計算を行う大まかなフローの例を示す．まず計算したい分子の情報（分子を構成する原子種やそれぞれの原子の位置座標など）および計算条件（波動関数を表現する関数（基底関数）のセットなど）を指定し，図1のシュレーディンガー方程式に現れるハミルトニアン$H$を計算する．これはたとえばpyscfやGAMESSといった量子化学計算プログラムを用いて，古典コンピュータにおいて行われる．その後，計算されたハミルトニアン$H$を量子回路で扱える形に古典コンピュータで変換を行い，量子コンピュータもしくはシミュレータ上でシュレーディンガー方程式を解くことで，エネルギーや波動関数，またその他の物理量を得るという流れである．現在では，前述したIBM社のQiskitやGoogle社のCirqなどのライブラリにこのような量子化学計算ツールが組み込まれており，専門知識がなくとも簡単に計算を行うことができる．また，商用ソフトウェアも開発されている．

ではどのような方針（アルゴリズム）で量子回路を作成すれば「よい」電子の波動関数が構築できるのか（または精密な量子化学計算を行えるのか）というのが問題となる．これは現在世界中の研究者が取り組んでいる非常にアクティブな研究領域であり，詳細な説明は量子力学・量子化学の知識が必要であるため，本稿では最小限の概念的な説明にとどめ（日本語の丁寧な解説として文献[2]がある），以下の章では専門知識がない読者でも現在および将来の量子コンピュータを用いた量子化学計算がどのようなものであるかの雰囲気が理解できるような説明を試みる．2章ではNISQと呼ばれる現在の量子コンピュータにおける量子化学計算の簡単な説明と，弊社の材料シミュレーションに向けた取り組みを述べる．3章では，最近の量子コンピュータのハードウェアの進展に触れ，近未来の量子コンピュータによりどのように材料計算が変わるか，を説明する．4章で将来に向けての展望を述べる．

2．現在の量子コンピュータを用いた材料シミュレーション

2.1　ノイズのある量子コンピュータ（NISQ）を用いた量子化学計算の概要

現在の量子コンピュータはNISQ（Noisy Intermediate-Scale Quantum computer，ノイズのある中規模スケール量子コンピュータ）と呼ばれ，量子ビットの数は数十～数百個程度であり，また測定結果はノイズを含んだものとなる，という特徴がある．ここでノイズがある，ということはどういうことかというと，たとえば前述の図4で示される量子回路の測定結果は，理想的な（ノイズのない）量子コンピュータであれば「0011」「0101」というビット列のどちらかのみが観測されるはずであるが，ノイズの影響によりそれ以外のビット列（たとえば「1000」「0111」など）も予期せず観測されてしまうことをいう．このノイズの影響は基本的に量子回路中の量子ビットの数および量子ゲートの数が多いほど顕著になるため，意味のある計算ができる（結果がノイズに埋もれない）サイズには強い制限が付く．

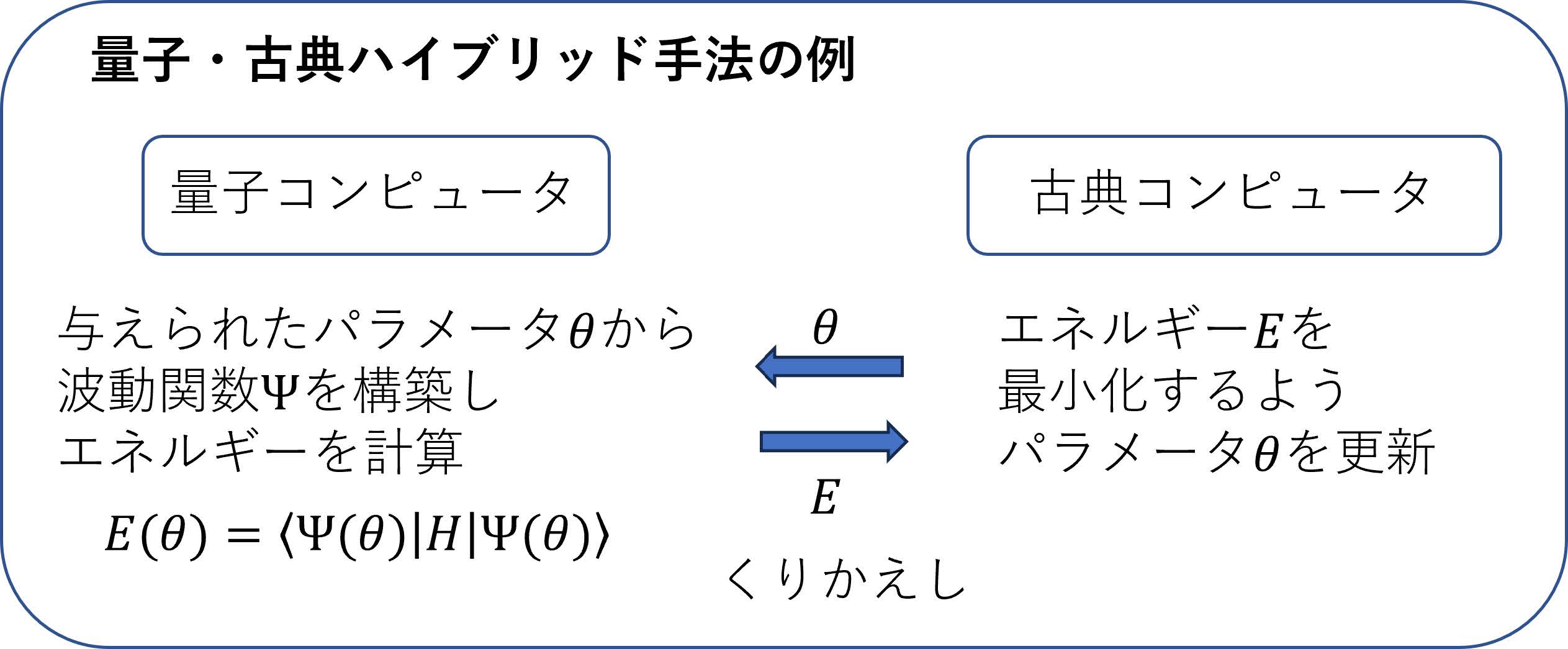
これまでに行われてきたノイズのある量子コンピュータを用いた量子化学計算で最もポピュラーなものはVariational Quantum Eigensolver（VQE，変分量子固有値ソルバー）と呼ばれる手法である．VQEでは，波動関数を構築する量子回路中のゲートの中に含まれる回転角などのパラメータ（たとえば図4の$\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}$）を，量子コンピュータで計算されるエネルギーが最小になるように古典コンピュータで調整する（「最適化する」と呼ぶ）ことを繰り返し行うことで，正しい波動関数を求める（図6）．このような量子コンピュータと古典コンピュータの両方を活用する手法は「量子・古典ハイブリッド手法」と呼ばれ，量子化学だけでなく，量子コンピュータを使った機械学習や，組合せ最適化等においても用いられている．この方法が現在のノイズのある量子コンピュータで用いられる理由は，比較的用いられるゲートの数が少なくて済み，ノイズの影響が抑えられること，また量子回路に含まれるパラメータ最適化は古典コンピュータの既存のライブラリを用いることができるため，量子コンピュータで複雑な処理が要らないこと，などが挙げられる．

2.2　量子コンピュータ実機を用いた感光性材料シミュレーション

さて，NISQにおける量子化学計算の概要を説明したところで，我々がIBM社と共同で実際に量子コンピュータ実機を用いて行った半導体製造プロセスで用いられる材料の量子化学計算を紹介したい[3]．この研究では，半導体製造におけるリソグラフィープロセスで用いられるフォトレジスト中の酸発生剤（Photo-acid generator，PAG）と呼ばれる材料をターゲットとして計算を行った．

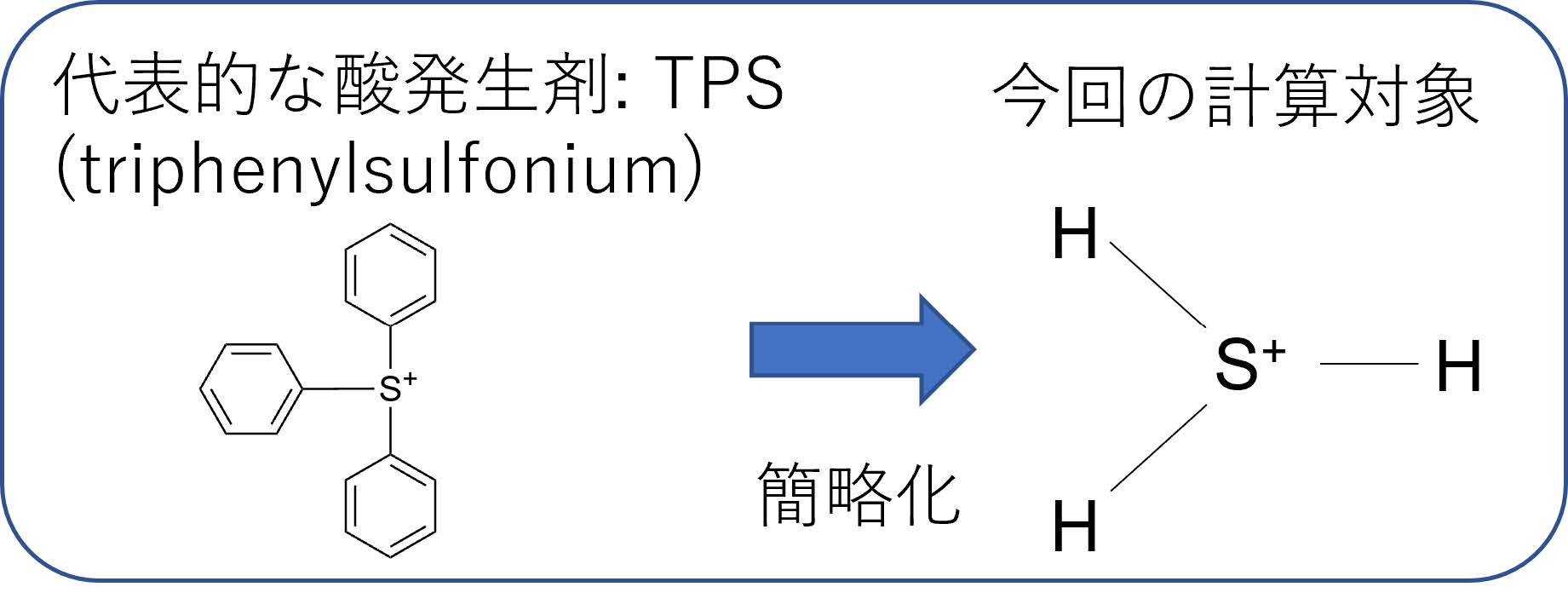
酸発生剤は光の照射により酸を発生させる分子であり，フォトレジストの溶解性を変化させるために用いられる．光照射により酸発生剤は基底状態から励起状態への遷移および解離反応（分子が分裂する反応）を含む複雑な化学反応を起こすため，古典コンピュータによるシミュレーションでその挙動を完全に予測することは難しい．本研究では，量子コンピュータを将来の半導体プロセス材料の光反応予測に役立てるべく，代表的な酸発生剤であるTPS（triphenylsulfonium）を簡略化したモデルとしてH₃S⁺というイオン（図7）をターゲットとして量子コンピュータ実機を用いた量子化学計算を行った．この簡略化されたイオンはTPSの3つのフェニル基を水素で置換した非常に単純な構造をしているが，このような極端に簡略化した分子でも，ある程度意味のある量子化学計算をするためには分子軌道12個，すなわち12量子ビット程度が必要で，この研究を行った2022年当時のノイズのある量子コンピュータ実機では計算結果がノイズに埋もれてしまい，正確な結果が得られなかった．

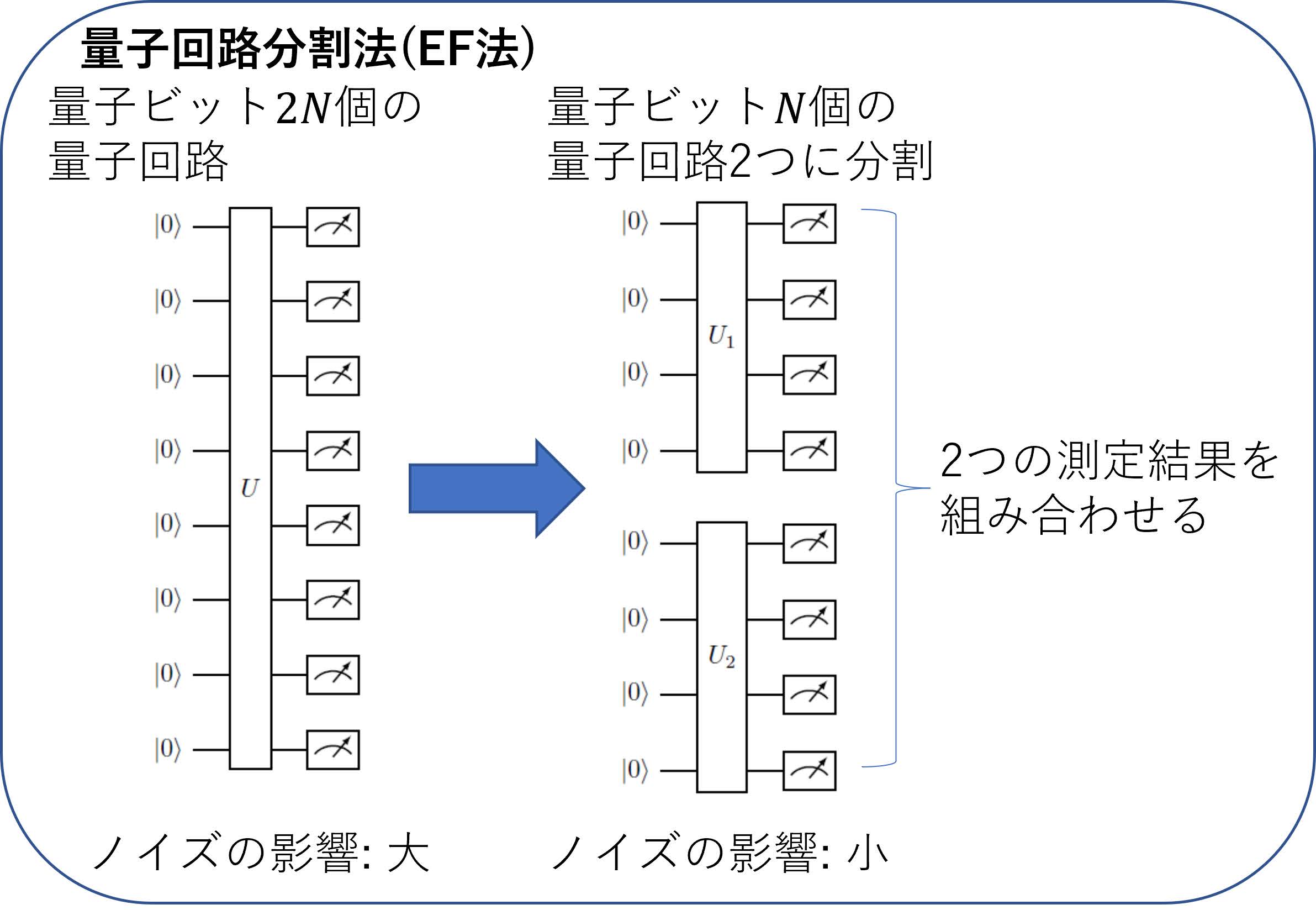
そこでこの研究では，ノイズの影響を回避するために，Entanglement Forging法（以下EF法）と呼ばれる量子回路分割手法を適用した．EF法の要点は，$2N$個の量子ビットが必要な量子回路を$N$個の量子ビットを含む2つの量子回路に分割し，2つの量子回路で得られた測定結果を巧妙に古典コンピュータで足し合わせて$2N$量子ビット相当の計算を行うというテクニックである（図8）．今の計算では本来12量子ビットを含んだ量子回路が必要であったのが，EF法を用いることで6個の量子ビットからなる量子回路だけの測定で済むことになり，量子回路が単純化され，ノイズの影響を軽減することができる．

この手法を用いて行った計算結果の例を図9に示す．図9（a）と（b）はH₃S⁺イオン中の1つの水素（H）原子と硫黄（S）原子の距離Rを変化させたものを横軸として，分子の基底状態および励起状態のエネルギーを縦軸にプロットしたもので，分子のポテンシャル曲面と呼ばれる（専門的な話になるが，（a）と（b）の違いは電子の持つ内部自由度であるスピン状態の違いを表し，（a）はスピン一重項，（b）はスピン三重項と呼ばれる状態である）．図に示されているのはこのイオンを厳密に計算した場合のエネルギーの値（FCI），古典コンピュータ上でのシミュレータにより計算された値（statevector，qasm）および量子コンピュータ実機計算（hardware）の結果である．このエネルギースケールでは厳密解，量子コンピュータ実機およびシミュレータの結果が良い一致を示しており，ノイズの影響が抑えられていることが分かる．

図の（c），（d）はさらに専門的な話になるが，分離（解離）する水素原子の電荷をそれぞれスピン一重項・三重項に対してプロットしたものである．原子間距離Rが大きなところで電荷が+1の場合は水素はH₃S⁺ → H₂S + H⁺のように陽イオン（H⁺）として解離し，また電荷が0の場合は水素はH₃S⁺ → H₂S⁺ + Hのように電気的に中性な原子のまま解離するなど，量子化学計算により化学反応の有用な知見を得ることができるのである．今回の結果は新しい結果ではないが，当時のノイズのある量子コンピュータ実機でも材料のモデル分子の性質について厳密解と一致する意味のあるシミュレーション結果が得られた，ということが重要なマイルストーンと考えている．

2.3　これまでの学び

この章では現在のノイズのある量子コンピュータ（NISQ）での量子化学計算について説明した．現在では，VQEなどのNISQ向けアルゴリズムや，関連するテクニックについての多くの知見が蓄えられてきており，弊社もこれまでに大学・企業との共同研究を通じて，VQEを利用した新規量子化学アルゴリズムの提案[4,5,6]，固体材料向けの計算[7,8]，表現能力が高い量子ゲート開発[9,10]などを行ってきた．

世界中で量子コンピュータ実機を用いた実証実験も数多く行われてきたが，前節で示したように，実機での計算においては「ノイズをどう取り除き，意味のある結果を得ることができるか？」ということに主眼がおかれてきた．詳細については本稿の範囲を超えるが，前節の我々の材料の計算においても，量子回路分割法に加えてノイズのある結果から後処理により正しい結果を得るさまざまなテクニック（これらの手法はerror mitigation，エラー緩和法と呼ばれている）が使われており，実機計算を通じてこのようなノウハウを吸収できたことは非常に価値のある経験であった．

では，NISQを用いたこれらの取り組みの延長上に，量子コンピュータを実際の素材開発シミュレーションに活用できる未来があるか？というと，答えはそう簡単ではないことが分かっている．問題はいくつかあるが，その中でも大きなものとしては，

• 前述のようにNISQにおいては量子ビットを増やしていくと（EF法のような回路分割手法を用いても）測定結果中のノイズが大きくなり厳密な答えが埋もれてしまう
• 量子ビットが大きくなると所望の答えを表現するのに必要な量子回路も複雑となりその回路を構成するパラメータを最適化するのが困難になる
• エネルギーを精度よく求めるためには量子回路の測定回数が大きくなりすぎる

などの点があげられる．そのため，VQEを用いた量子化学計算は実用上20量子ビット程度以上の計算を行うことは難しくなり，この程度の規模であればノートPCやワークステーションによりまったく同じ計算がシミュレータを使ってノイズなしに実行可能である．つまり，これまでに報告されてきたNISQを用いた研究はあくまで量子ハードウェアの性能テストや理論の実証実験にすぎないのである．

では世界中の大学および企業が取り組んできた，今までの研究は無駄なのであろうか？というと決してそうではない．実際にクラウド上で動く量子コンピュータ実機とQiskitのようなライブラリが提供されたことで，企業・大学・研究所が量子コンピュータの重要性を認識しながら基本概念を学ぶ土台が整い，産学官の連携を促すコンソーシアムなどが多数設立された．また世界中の研究者によってアルゴリズムや基礎理論が目覚ましい進展を遂げ，人類が量子の時代へと備える「準備期間」として大きな意義があったと思われる．また，本章で紹介したVQEのような量子・古典ハイブリッド手法は気軽にノートPC等で動かすことができるため量子アルゴリズムの基礎を学ぶ教材として最適であり，しばらくは学生・若手エンジニアの入門的教材としてなくなることはないと思われる．

3．量子ハードウェアの進展：ユーティリティ時代・FTQC時代における材料シミュレーション

3.1　量子ハードウェアの進展

前章で述べたように，これまでに行われてきたシミュレーションは，我々の半導体材料の実証実験を含め，数量子ビット～十数個のものがほとんどである．この程度の量子ビットは，古典コンピュータで問題なく厳密にシミュレーションが可能である（たとえば10量子ビットの量子回路のシミュレーションは，サイズ1024×1024の行列とベクトルの演算の繰り返しである）ため，量子コンピュータを使った意味のある計算，そして産業応用への道のりはまだまだ遠いであろうと考えられていた．

しかし，近年のハードウェアの進歩に伴いこの状況が変わりつつある．そのきっかけの1つとなったのが，IBM社が2023年に発表した論文[11]であり，簡単に内容をまとめると「あるモデル（スピンモデル）のシミュレーションについて，127量子ビット（古典コンピュータの10²⁷テラバイト程度に相当）を用いた超伝導型量子コンピュータ実機の結果が，汎用的な既存の古典アルゴリズムの結果の精度を上回った」という報告である．この論文は量子コンピュータが古典コンピュータで計算不可能な領域についに到達した，という結果ではない（汎用アルゴリズムでなく，このモデルに特化したアルゴリズムを用いることで，古典コンピュータにおいても量子コンピュータの結果を再現できることがいくつかのグループにより報告されている）．しかしながら，この結果はこれまで数量子ビット程度の計算しかできないと思われていた量子コンピュータが，古典コンピュータの最先端アルゴリズムの精度に追いつきつつあるということを示唆している．この研究に触発されて多くの研究グループが数十～百量子ビットを使った計算結果を報告してきており，これまでのトイモデル実証実験の時代から，数十～百量子ビットを使った「有用性（utility）」のあるアプリケーションを探索するという新たなフェーズに入ってきたことがうかがえる．

また，このようなハードウェアの進歩に加えて，量子誤り訂正（Quantum Error Correction）理論に関しても大きな進展があった．量子誤り訂正についての説明は本稿の範囲を超えるために説明を省くが，「量子ビットの状態にノイズによりエラーが起こった場合にそれを自動的に検出し正しい状態に訂正する一連の仕組み」だと思っていただきたい．量子誤り訂正機能を備えた量子コンピュータはFTQC（Fault-Tolerant Quantum Computer）と呼ばれ，これまでの認識ではその実現は2040年とも2050年ともいわれていたが，近年のハードウェアおよび誤り訂正理論の進展により，各ハードウェアベンダーが2030年前後にFTQC量子コンピュータをリリースするというロードマップを公開している．本章では，このようなハードウェアの進化に伴い量子化学シミュレーションがどのように変化していくか，ということを概観する．

3.2　数十～百量子ビットを用いた量子化学計算

ハードウェアの進展により量子コンピュータ実機中の量子ビットの数も増加しており，たとえば超伝導型量子コンピュータでは100を超える量子ビットを持つマシンが提供されている．表1で示したように，たとえば100量子ビットで「原理的に」表現できる状態ははるかに古典コンピュータの能力を上回るものの，前章で述べたようなノイズの問題により量子回路の中で用いることのできる量子ゲートの数には限界があるため，このような大量の量子ビットを有効活用できるアルゴリズムは現状あまり存在していない．

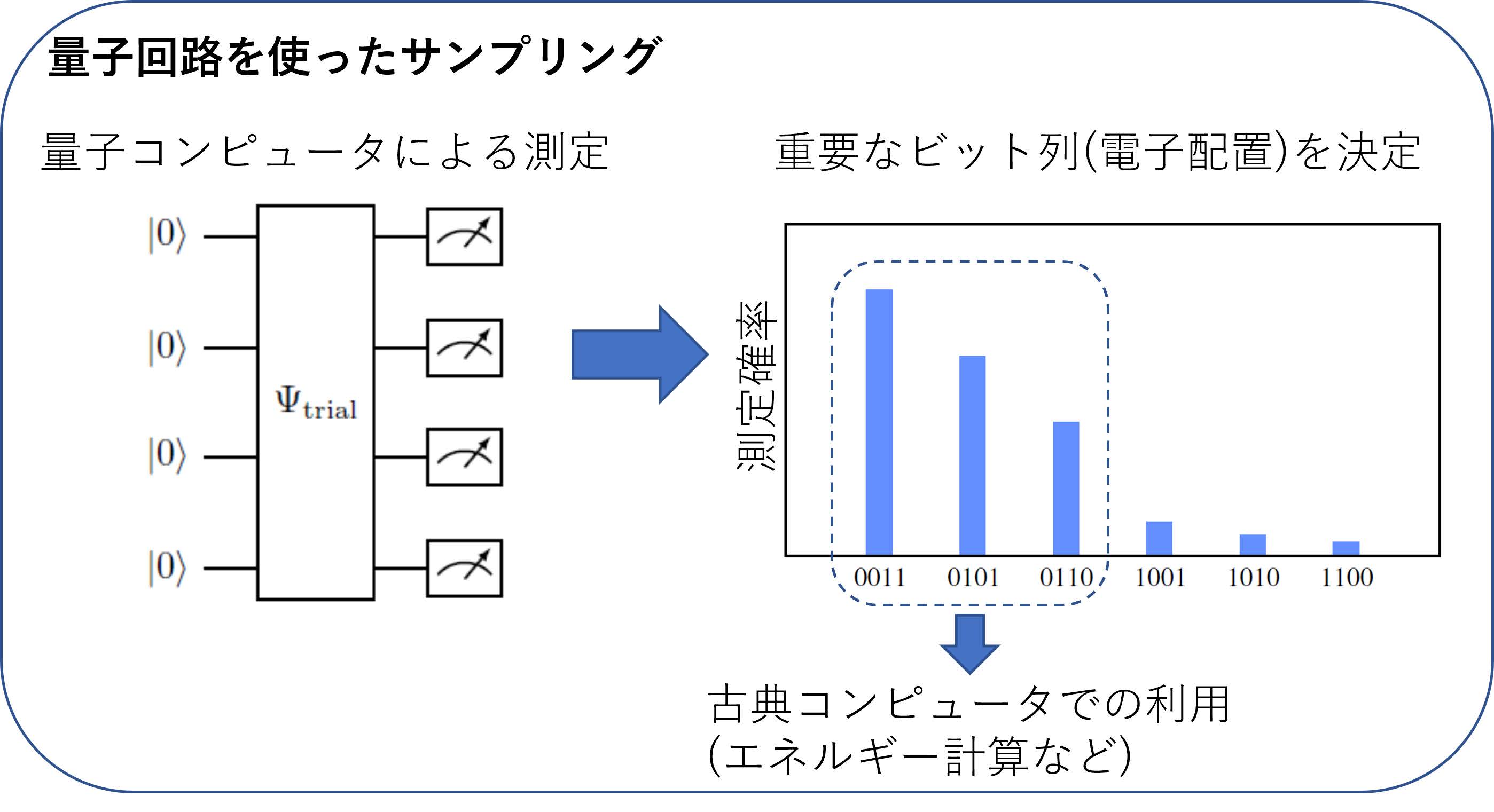
多数の量子ビットを活用して量子化学計算を行う1つの試みとして，QunaSys社と大阪大学が2022年に提案したQuantum Sampling CI法（QSCI法）と呼ばれる量子化学計算手法がある[12]．このアプローチは，量子コンピュータを「波動関数の全電子配置の組の中から，重要なものを提案する機械」としてのみ用い，その提案された電子配置を使って，エネルギー計算は古典コンピュータで行う，というサンプリングベースの手法である（図10）．たとえば図2で表されるように，電子の波動関数が4量子ビットで表され（分子軌道4つ），その中の2つを電子が占有する場合，そのビット列の中で0が2つ，1が2つ入る組合せは全部で6個ある．QSCI法では，図10で示されるように，適当な量子回路を構築し，その測定で得られたビット列を確率の高い方から$d$個を選ぶ（$d$の値はユーザーが指定，図10では$d=3$）．その後，選ばれた$d$個の電子配置のみを用いて分子のエネルギーを古典コンピュータで計算する，というものである．この方法は前章で紹介したVQEなどと異なり，量子コンピュータは電子配置のサンプリングのみに使い，エネルギーの評価は古典コンピュータで行うためにノイズの影響を取り除きやすい方法であり，原理的に多数の量子ビットを活用することができる．ではどのような量子回路を構築すればよい電子配置を得ることができるか問題となる．この問題については今後の研究も待たれるが，QunaSys社，大阪大学と弊社の共同研究により，サンプリングする量子回路のゲートを問題とする分子に応じて逐次的に構築する方法が提案されている[13]．

2024年にはIBM社・理研のグループがこのQSCI法の考えをベースとしたサンプリング手法を用い，理研のスーパーコンピュータである「富岳」と連携して最大77量子ビット（古典コンピュータ10¹²テラバイト程度に相当）という巨大な量子コンピュータ実機リソースを用いた量子化学計算結果を発表した[14]．発表された計算結果はまだ古典コンピュータのアルゴリズムの精度を超えてはいないものの，77量子ビットという古典コンピュータでは容易に到達不可能なリソースを使った計算結果が得られたことは，量子ハードウェアおよび量子アルゴリズムの驚異的な進展を感じさせるものである．また，この研究で示された「量子コンピュータとスーパーコンピュータの連携」は将来の大規模材料シミュレーションの1つの方向性であり，たとえば物質中の電子の量子化学計算（シュレーディンガー方程式）は量子コンピュータで行いつつ，分子動力学シミュレーションや機械学習をスーパーコンピュータで行う，などいろいろ有用なアプリケーションの可能性を考えることができ，今後の発展を期待したい分野である．

3.3　FTQC時代の材料シミュレーション

この章の最後として，誤り訂正機能付き量子コンピュータ（FTQC）向けのアルゴリズムの進展について述べる．そもそも誤り訂正があるとなにがうれしいのか？ということであるが，ごく簡単にいうと「複雑な長い量子回路を実行しても正確な結果を得られる」ということである．たとえば因数分解を量子コンピュータで行うアルゴリズムなどは量子回路が複雑になるため，その実現にはFTQCが必要であると言われている．

量子化学計算におけるFTQC向けの代表的なアルゴリズムとしては「量子位相推定」と呼ばれる手法があり，ある意味量子化学計算の究極の手法であると思われている．ごく簡単にその原理を述べると，波動関数 Ψにハミルトニアン$H$を$e^{iHt}$の形で作用させる（$t$は仮想的な時間）と，その波動関数のエネルギーを$E$として波動関数は$e^{iEt}$Ψのように変化する．ここで係数として現れる$e^{iEt}(=\cos Et+i\sin Et)$で表されるのが波動関数の「位相」と呼ばれるもので，量子位相推定というアルゴリズムで計算することができ，その位相から波動関数のエネルギー$E$が分かる，というからくりである（図11）．詳述は控えるが，前章で紹介したVQEなどのアルゴリズムと違い，量子位相推定において求められるエネルギーは近似的なものではなく，厳密な値が取り出せるということが大事である．量子位相推定については多くの研究がなされており，効率的アルゴリズムが数多く提案されている．2024年現在，弊社を含む9社が参画している慶應義塾大学量子コンピューティングセンターの量子化学チームにおいては，現在特任准教授の杉崎研司氏を中心として量子位相推定のアイディアに基づいた多方面からの研究が精力的に行われている．最近の研究例を述べると

• 励起エネルギーや安定分子構造を求めるのに必要な原子に働く力の計算アルゴリズムの提案[15,16]
• 光吸収スペクトルなどの計算への応用[17]
• IBM社の超伝導型量子コンピュータ実機を用いた最大33量子ビットを用いた量子位相推定の実機検証[18]

などである．量子位相推定に代表されるFTQC向けのアルゴリズムは本当の意味で古典コンピュータによる計算を上回る可能性を持ち，実現されれば材料シミュレーションへのインパクトは計り知れない．量子ハードウェアおよび誤り訂正理論の進展により，そのような未来が到来することを心より期待したい．

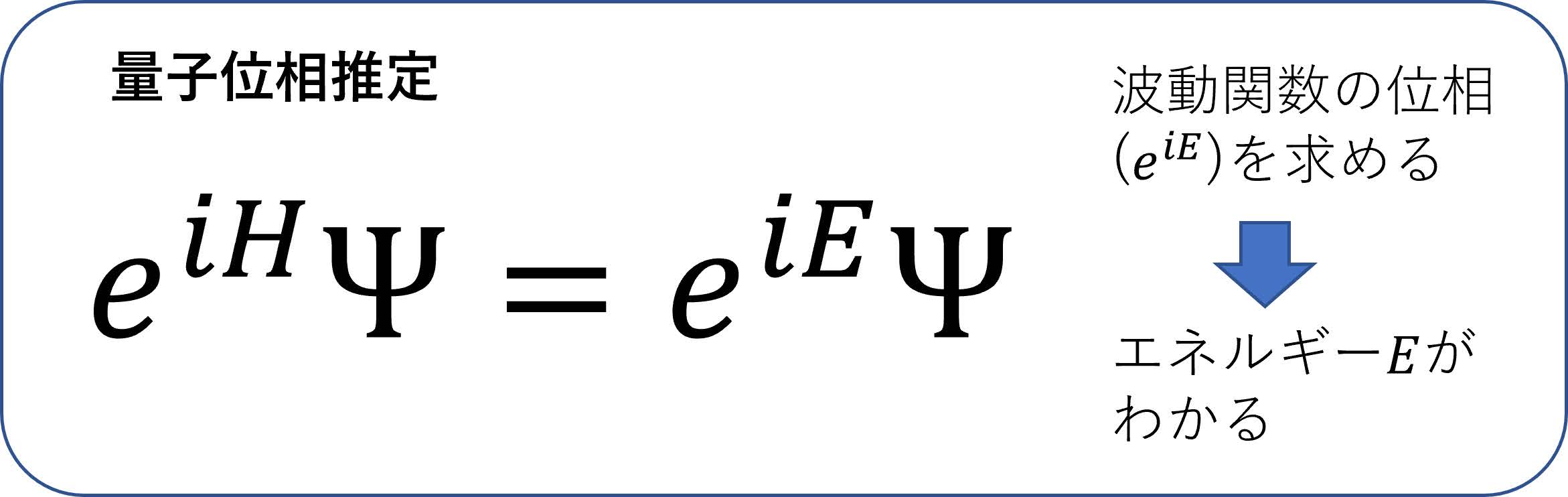
4．展望：未来の材料開発にむけて

以上，材料シミュレーションに用いられる量子化学計算の概念とその難しさ，現在のノイズのある量子コンピュータを用いた量子化学計算の取り組み，そして将来の量子化学シミュレーションについて概説した．量子コンピュータ実機の登場以来，我々は量子アルゴリズムおよび量子ハードウエアの目覚ましい進展を目の当たりにし，そして数年後には誤り訂正付きの量子コンピュータの公開が予定されている，とまさに時代の転換期を生きていることを実感する．

では量子コンピュータを活用した未来の材料開発はどのようになるであろうか？　これまで精密な測定や計算ができなかったような現象が，コンピュータ上で再現できるようになった暁には，これまで制御が難しかった反応などが産業的に活用できるようになるかもしれない．そのような現象を見つけ，創り出していくことが重要であると思われる．

量子コンピュータの産業応用の実現のためには，大学・研究所・企業の連携が不可欠である．弊社の参画する慶應義塾大学量子コンピューティングセンターでは，競合企業である銀行・化学メーカの研究員が共通の問題に取り組み，「どのような問題が量子でスピードアップするのか」・「どのような問題が解けるようになるとうれしいか」という議論が毎日交わされ，共著論文や特許を作成している．このようなコンソーシアムが日本全体で発展することを期待したい．また，近い将来には，研究成果をどのように各企業および日本全体の利益に結び付けるか？という話し合いもよりオープンに行われる必要があると思われる．