マルチエージェント・シミュレーションを用いたイベント観客の分散退場が駅の混雑に与える影響の分析
Analyzing Impact of Controlled Visitor Exit for Station Congestion using Multi-Agent Simulation
1. はじめに
音楽ライブやスポーツの試合といった大規模なイベント時には,数多くの観客が開催地に集中し混雑が発生する.人混みでは押し合いへし合いによって転倒の危険性が高まり,雑踏事故につながる恐れがある.日本国内に限定しても,死者が報告されている雑踏事故の事例は1950年以降で10件以上存在し[1],2001年に発生した明石歩道橋事故では,イベントの開催地と鉄道の最寄り駅を結ぶ歩道橋において,駅に向かう人々と駅から出る人々をそれぞれ適切に誘導できず,異常な混雑が発生した結果多くの死傷者が発生した[1].このような事例から,イベント時には観客の交通手段となる周辺の鉄道駅への影響を考慮する重要性が報告されている[2], [3].混雑による事故を未然に防ぐ対策の1つとして,「分散退場」の有効性が指摘されている[1].分散退場とは,観客を一斉に退場させるのではなく,時間差を設けて段階的に退場を案内することで,混雑緩和を図る方法である.観客を一定時間あたりに何人退場させるか,という観客の流出速度を適切に設計することで,混雑緩和を実現する.しかし,駅の混雑緩和に向けて観客の流出速度を決定するには,各駅の利用人数を正確に把握し,さらには観客の流出速度が周辺駅の混雑に与える影響を試算する必要がある.流出速度が大きいことは一度に多くの観客に退場を案内することと同義であり,各駅の混雑が深刻となる恐れがある.
分散退場における流出速度を検討するアプローチとして,多数のイベントで実際に流出速度を変更して各地の混雑のデータを収集する方法,あるいは妥当な仮説を立ててシミュレーションで机上検討をする方法,の2つが考えられる.前者の課題として,曜日や天気,社会情勢など,イベント以外の要素による影響を切り分けながら因果を明らかにする必要がある.また,収集したデータを基に,機械学習で最適な流出速度を推論する方法も考えられるが,学習に足る数の大規模イベントのデータを収集するのは現実的ではない.一方,後者の方法では,現実では試すことが難しいパターン数の検証が可能であり,結果を得るまでに要する時間は,シミュレーションの計算時間のみである.そのため,雑踏事故等の対策が必要とされるイベント運営者や鉄道会社等の交通事業者に対して,混雑の分散に有効な示唆を素早く提供できる,といった利点がある.
シミュレーションを活用して,会場や駅の混雑を軽減するための流出速度を導くためには,混雑に影響を及ぼす要素を適切にモデル化する必要がある.観客の動きのみをシミュレーションに反映し,その結果から流出速度を算出した場合,非観客の鉄道利用が考慮されていないため,駅では予想以上の混雑が発生する可能性がある.したがって,駅の混雑をモデル化するには,観客と非観客の両方の動きを捉えることが求められる.観客の動きについては,流出速度に応じて各時刻における駅の利用者数は変動する.一方,非観客の鉄道利用者の動きについては,イベントとは無関係に時間帯ごとに駅の利用者数が異なる.そのため,駅の混雑を緩和するために分散退場時の流出速度を決定するには,流出速度に応じた観客の動きと,各時間帯の非観客の鉄道利用者の動きをモデル化する必要がある.
イベント時の会場周辺の駅の混雑をシミュレーションするには,観客と非観客の鉄道利用者,両方の移動を捉えた上で,「流出速度」や「イベントの開催時刻」といった条件を変更した際に,混雑がどれだけ変動するかを検証する.従来研究として,イベント会場内の混雑緩和に向けて,シミュレーションを活用する事例は報告されており[4], [5],定点観測するセンサを用いて人々の動きを捉えている.一方で,会場周辺の混雑を対象として検証した事例は報告されていない.これは,改札データやカメラで断面交通量を観測する方法では,コストを要することや観客と非観客の判別が困難なこと,またGPS信号を用いる方法では,特に地下鉄を対象とする場合において位置情報の取得が困難であるといった背景が原因と考えられる.
本稿では,周辺交通の混雑対策に向けたシミュレーションを行ううえで課題となる,人々の位置情報の収集という問題に対して,携帯電話基地局のネットワークデータを利用することを提案する.ここでのネットワークデータとは,各携帯端末と携帯電話基地局の間で行われた通信のログの一種である.本データから読み取れる各地点の滞在傾向から,観客と非観客を判別し,この結果を基に分散退場による各地点の混雑推移を再現するシミュレータを構築する.本シミュレータを用いて,複数のイベント終了時刻について分散退場における流出速度を変えることで周辺駅の混雑へ与える影響を確認する.
本稿の主な貢献は,以下の2点である.
- ・観客と非観客の両方の動きを考慮し,イベント後における駅の混雑の精緻な把握を可能にした.
- ・携帯電話のネットワークデータとMASを組み合わせることで,分散退場が駅の混雑に与える影響を試算した.
本稿の構成は以下のとおりである.まず2章で関連研究を概観し,3章で提案手法を説明する.4章で実データを用いた評価実験の内容と結果を示し,5章で得られた知見について説明する.最後にまとめと今後の展望を述べる.
2. 関連研究
群衆シミュレーションは,物理指向とマルチエージェント指向の2種類に大別される[6].物理指向のシミュレーションでは,歩行者の移動を流体力学等の物理法則に基づくものとして計算する[7], [8].一方,マルチエージェントに基づくシミュレーションは,セルラーオートマトンモデルやエージェントベースモデルを用いて実装される[9], [10].これらのうち,マルチエージェント指向のエージェントベースモデルは,各エージェントの特性を個別に定義可能,周辺環境との相互作用を扱えるといった利点を持つ[6].
イベント時の群衆シミュレーションとして,エージェントベースモデルを活用するには,人々をエージェントと見立て,各地の混雑を再現するように各エージェントの出発地や目的地,歩行速度といった行動モデルを定義する.イベント時の群衆シミュレーションは以下の2つの観点で分類できる.
- ・エージェントの対象:観客のみvs.観客以外も含む
- ・シミュレーションの範囲:会場内vs.会場外
観客の会場内の動きをシミュレーションした事例として,Zhonghuaら[4]による,会場内の計測データを用いて会場内の混雑を緩和する誘導策を導出した研究が挙げられる.また,分散退場に焦点を当てた研究として,実際のイベントの計測データとシミュレーションを基に,分散退場が会場内の混雑に与える効果を定量的に明らかにしたもの[5]や,Choiら[11]による会場内における観客の動線や入場間隔をシミュレーションで探索し,感染対策に有用な結果を提示したものが報告されている.さらに,イベント時における会場から駅までの道路混雑について,ステレオカメラで取得した観客の歩行速度をシミュレーションモデルに実装した研究も報告されている[12].
一方で,会場周辺の駅の混雑をモデル化したシミュレーション事例は筆者らの知る限り報告されていない.これは,1章で述べたとおり,駅の混雑を分析するには観客以外の動きも考慮する必要があり,地下鉄駅ではGPS信号の取得が困難になることや,定点カメラでは観客と非観客の判別ができない,といった背景が原因と考えられる.
3. 手法
シミュレーション条件の理解を容易にするため,モデルの標準的な記述手法としてODD(Overview, Design concepts and Details)プロトコルがある[13].ODDは,目的,エンティティ,デザインコンセプト,プロセス概要,初期化,入力データ,サブモデルの7要素で構成される.本稿ではODDプロトコルに沿ってシミュレーションモデルを説明する.
3.1 Overview: 目的
本シミュレーションの目的は,分散退場における流出速度の違いによる会場周辺駅の混雑への影響を確認することである.具体的には,会場からの流出速度,およびイベント終了時刻を変化させた際に,会場周辺の駅の混雑の変化を検証する.この検証は,非観客の鉄道利用者の需要はイベントとは関係なく発生するため,イベントの開催時刻によって流出速度の最適値は異なるという仮説に基づくものである.
評価対象とするエリアは,図1に示すように国立競技場とその周辺駅を含む1.4 km四方の範囲とした.国立競技場の近くには,徒歩圏内に4路線5駅が存在する.地理データには,OpenStreetMap [14]を採用した.シミュレーションソフトウェアには,株式会社スペースタイムエンジニアリングが開発したScenargie®を使用した[15].エージェントは状態変数として,歩行速度,行動開始時刻,乗車駅,下車駅を有する.観客を模したエージェントは,行動開始時刻に,会場から出発駅まで道路ネットワークに沿って,平均0.8 m/s,標準偏差0.2 m/sの正規分布に従う歩行速度で移動する.なお,このパラメータを設定した経緯については5.2章にて後述する.
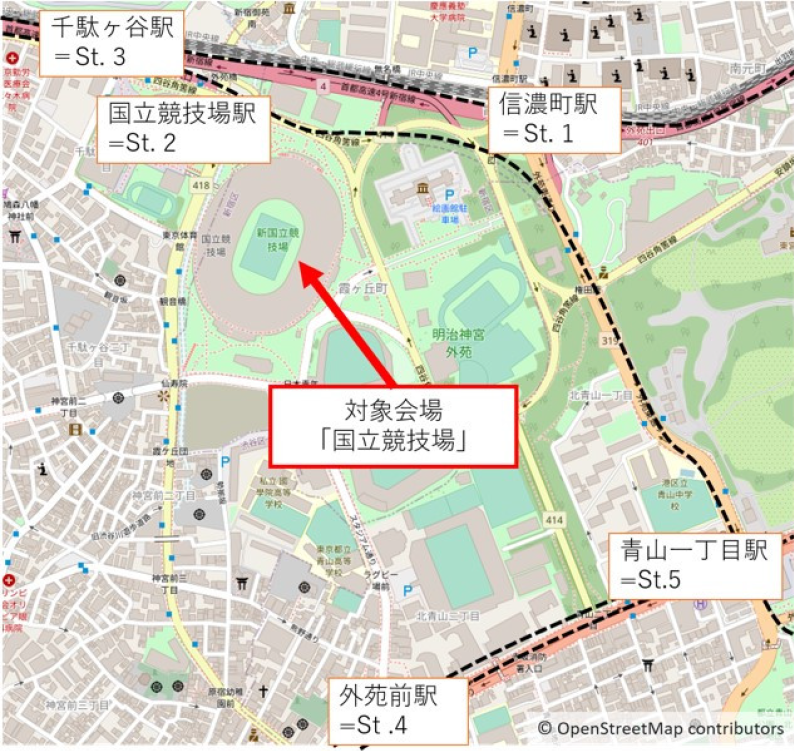
Fig. 1 Area Subject to Verification.
電車は時刻表に基づき運行し,乗車駅に到着したエージェントは,次の電車が到着するまで駅で待機,電車が到着したら搭乗し下車駅で消滅する.非観客の鉄道利用者のエージェントは,乗車駅で発生し,電車に搭乗して移動した後,下車駅で消滅する.
3.2 Design concepts: 設計概念
分散退場とは,観客の座席などに応じて退場タイミングを順に案内することで,会場からの流出速度を制御し,混雑の軽減を図るものである.流出速度の制御の概要を図2に示す.青線は規制しない場合の流出速度,緑色の破線は規制退場を実施した場合の流出速度を示している.図2に示すように,流出速度を絞る目的として分散退場が採用される.
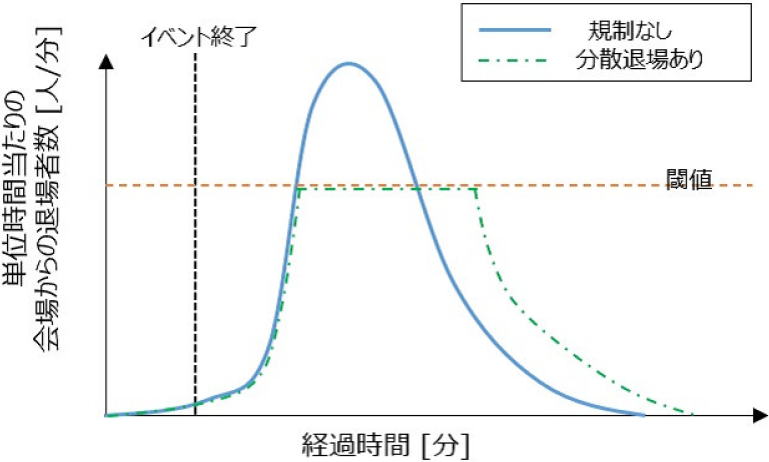
Fig. 2 Overview of controlled visitor exit.
本稿では,2022年5月29日に東京で開催されたラグビー試合「NTT JAPAN RUGBY LEAGUE ONE 2022 PLAY-OFFS FINAL」をシミュレーションの対象とする.本モデルにおいては,各エージェントの位置を記録し,駅や会場といった各建物単位で人口を集計することで,最適な流出速度を評価する.シミュレーションのタイムステップは2秒,人口の集計間隔は1分と設定した.
シミュレーションまでの概略を以下に示す.
- (1) 位置情報データに対してOrigin Destination(OD)データの分析を実施し,地点間の移動人数の集計値を算出.
- (2) ユーザを観客・非観客および鉄道利用者・非利用者の4象限のカテゴリに分け,それぞれの動きを再現するエージェントを作成.
- (3) MASで以下2つのパラメータを変化させて混雑の指標を算出.
(a)流出速度:観客エージェントの行動開始時刻を制御
(b)イベント終了時刻:非観客の鉄道利用者エージェントの行動開始時刻および人数が変化
3.3 Details: モデルの詳細
3.3.1 利用データの詳細
本シミュレーションでは,位置情報データとして,日本の通信事業者である株式会社NTTドコモの携帯電話ネットワークデータのうち,位置情報を分析に使用することに同意を得たユーザのデータのみを使用する.1章で述べたとおり,携帯電話のネットワークデータを利用することで地下鉄を含めた駅や施設の滞在を取得できる.これは,IMCS(Inbuilding Mobile Communication System)と呼ばれる屋内基地局への接続情報を利用することで,当該建物内の滞在判定が可能となるためである[16].プライバシー保護の観点から次項の処理により集計値のみを取り扱う.
3.3.2 エージェントタイプの分類
携帯電話のネットワークデータをシミュレーションのエージェントモデルに反映するうえで,観客か否か,そして鉄道を利用するか否かの観点で,ユーザを以下の4タイプに分類した.
i 観客×鉄道利用者タイプ
ii 観客×鉄道非利用者タイプ
iii 非観客×鉄道利用者タイプ
iv 非観客×鉄道非利用者タイプ
観客のユーザは,イベント中は会場内に滞在するため,観客の持つ端末は会場内のIMCSと連続して通信し,イベント終了後はユーザの場所に応じて駅や屋外の基地局と通信すると考えられる.一方,非観客のユーザは会場内のIMCSに接続することなく,ユーザの場所に応じて近隣の基地局と順次通信する.
また,鉄道利用者は,同一の鉄道路線上で少なくとも2駅を利用するため,鉄道利用者の持つ端末は同一の鉄道路線の2駅以上のIMCSに接続する.それに対し,鉄道非利用者は,駅のIMCSに接続されることは少ないと考えられる.以上の想定より,観客と非観客および鉄道利用者と非利用者を次のように判別した.
観客と非観客の判別
本項では,観客と非観客の判別方法について述べる.ユーザの状況と携帯電話基地局との接続関係をケースごとに整理すると図3のとおりとなる.観客は,必ずしもイベントの開始時刻から終了時刻まで参加して会場内のIMCSに接続されているとは限らない.具体的には,観客は開始時刻より後に来場したり終了時刻を待たずに退場したりするケースがある.また,イベント中は端末の電源を切る,もしくは機内モードにするといったケースが存在し,その間は携帯電話基地局と通信しないため,ネットワークデータが存在しない.このようなケースに該当するユーザを観客と判定しつつ,偶然会場周辺を通行した人を正しく非観客と判定する必要がある.
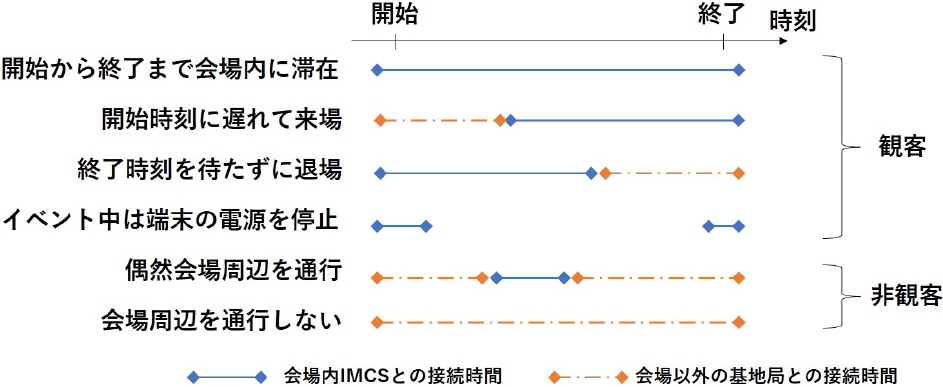
Fig. 3 Connection status between devices and IMCS in each case.
以上の背景から,採用した観客の判定方法のフローを図4に示す.まず,図1に示すエリアの携帯電話のネットワークデータのログについて,イベント開始時刻からイベント終了後3時間までのデータを抽出する.次に,イベントの開催中に会場のIMCSに接続した履歴のあるユーザを絞り込み,「会場内のIMCSに接続されていた時間」と「会場以外の基地局に接続されていた時間」を比較し,「会場内のIMCSに接続されていた時間」のほうが長かったユーザを観客として判定した.一方,前述の条件に満たなかったユーザを非観客として判別した.
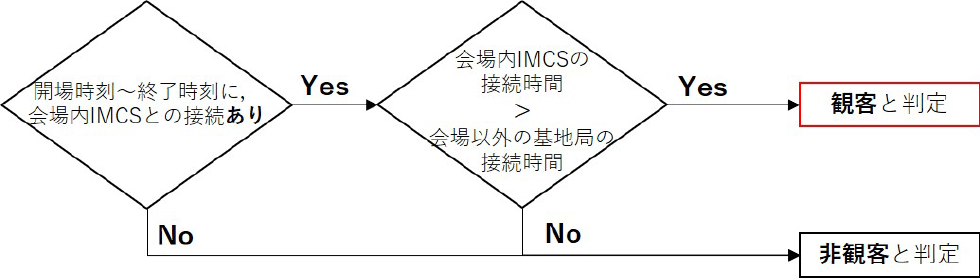
Fig. 4 Logic to determine visitors.
鉄道利用者と非鉄道利用者の判別
同一路線上の2駅以上について携帯電話基地局への接続が確認されたユーザを鉄道利用者と判定し,それ以外を非利用者と判定した.なお,鉄道利用者の乗車駅および下車駅については,図5の太枠で示す最寄の5駅のみを対象とした.便宜的に,以降の章では信濃町駅をSt.1,国立競技場駅をSt.2,千駄ケ谷駅をSt.3,外苑前駅をSt.4,青山一丁目駅をSt.5とする.ここで,最寄の5駅以外で乗車もしくは下車する場合は,シミュレーションの簡略化を目的として,図5に示すように各路線の最寄駅の隣の駅(代々木駅,表参道駅,四ツ谷駅,六本木駅,赤坂見附駅,永田町駅)で乗車もしくは下車するものとした.
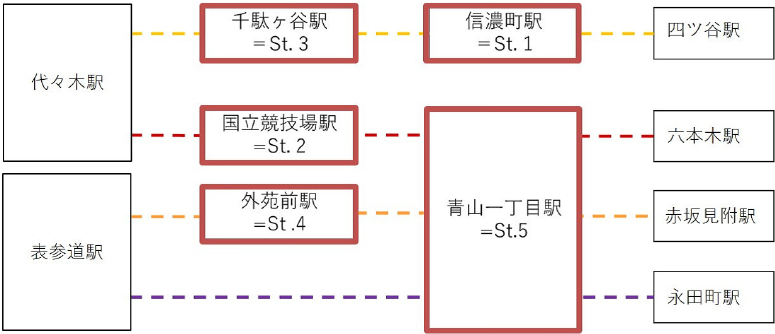
Fig. 5 Network of train staions.
たとえば,都営地下鉄大江戸線の国立競技場駅で乗車し,六本木駅で下車する場合は,「国立競技場駅乗車,六本木駅下車」となり,国立競技場駅で乗車し,麻布十番駅で下車する場合も,「国立競技場駅乗車,六本木駅下車」として取り扱う.ここで,会場周辺駅以外の人口が実態以上に多くなることが想定されるが,本稿では混雑が深刻な課題となる会場周辺駅に焦点を当てるため,上記の簡略化を行う.
なお,本稿では,鉄道駅の混雑に焦点を当てることから,鉄道の混雑に有意な影響を与えない非観客×鉄道非利用者タイプ(iv)のユーザはシミュレーションモデルの対象外とした.
3.3.3 各エージェントタイプのモデル定義
エージェントモデルの定義およびシミュレーションまでの全体像を図6に示す.
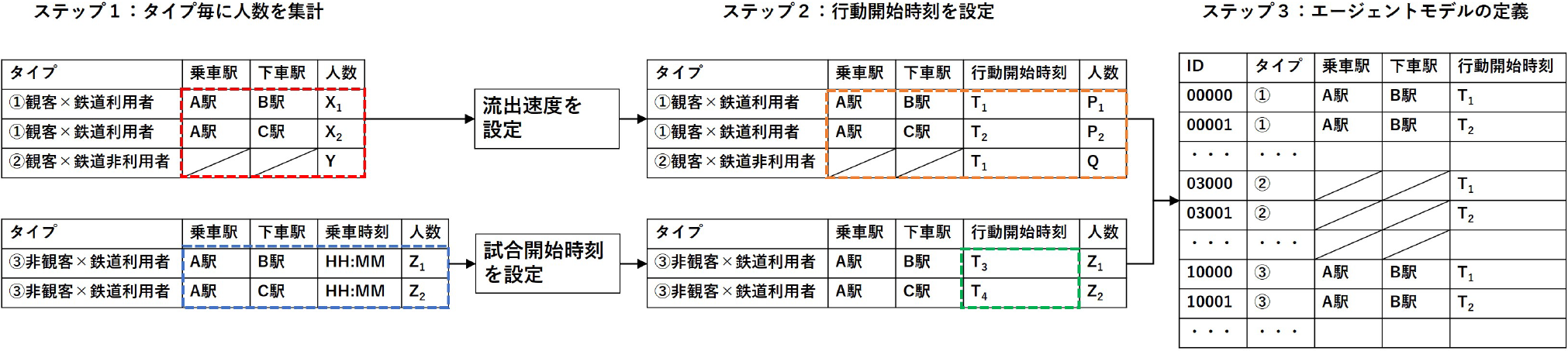
Fig. 6 Overview of model definition.
ステップ1:タイプごとに人数を集計
まず,観客×鉄道利用者タイプ(i)のユーザについて,携帯電話のネットワークデータに基づき,乗車駅と下車駅の組ごとに人数を集計し,観客×鉄道非利用者タイプ(ii)のユーザについても該当する人数を集計した.(図6赤枠)
非観客×鉄道利用者タイプ(iii)のユーザについては,「乗車駅,下車駅,乗車時刻」の組ごとに人数を集計した.(図6青枠)
集計の結果,各エージェントタイプの総数について,タイプ(i)は約25,000人,タイプ(ii)は約6,000人,そしてタイプ(iii)は約10万人となった.
ステップ2:行動開始時刻を設定
観客エージェント(i,ii)の行動開始時刻の設定方法について述べる.分散退場における流出速度の違いを検証するため,流出速度の上限として5段階の閾値を設定し,便宜上レベル1~5とした.レベル1は流出速度の上限が最も低く,長時間にわたって観客を退場させることとなる.レベルが上がるにつれて流出速度も増加することとし,流出速度の上限を満たすように,各時刻で出発する人数を設定した.(図6橙枠)なお,行動開始時刻はシミュレーション開始時刻(イベント開始時刻)からの経過時間[秒]とした.
次に,非観客×鉄道利用者エージェント(iii)の行動開始時刻の設定方法について述べる.観客と同様にシミュレーション開始時刻(イベント開始時刻)からの経過時間[秒]を行動開始時刻として設定する.本稿ではイベント開始時刻として15時,18時の2パターンを採用するが,乗車時刻がイベント開始時刻以前になっているエージェントは当該シミュレーションでは対象外とする.たとえば,乗車時刻が15時30分のエージェントは,15時イベント開始のパターンではシミュレーション時刻上で1800秒の時点で出現し下車駅に向かう.一方で,18時イベント開始のパターンでは,当該エージェントはすでに移動を完了しているため出現しない.
ステップ3:エージェントモデルの定義
ステップ2で算出した乗車駅,下車駅,行動開始時刻を基に,各人数の分だけエージェントを生成した.観客×鉄道利用者エージェント(i)は,シミュレーション開始と同時に出現し,下車駅に到着した時点で消滅する.観客×非鉄道利用者エージェント(ii)については,定義された行動開始時刻で会場を出発し,徒歩でランダムに指定した建物に向かい,到着したタイミングで消滅する.エージェントの出現時刻はシミュレーション開始と同時である.非観客×鉄道利用者エージェント(iii)は,行動開始時刻に出現し,下車駅に到着した時点で消滅する.
評価関数
各流出速度における混雑の指標を評価するため,本稿では混雑を下記の評価関数として定義した.\[f = k_1 \sum_{i=1}^n P_i + k_2 \sum_{i=1}^n T_i \](1)
ここで,nは周辺駅の数,Piは各駅のピーク人口[人],Tiは各駅の混雑解消時間[分],kiは各変数の重みを表しており,k1の単位は[人−1],k2の単位は[分−1]である.また,下付き文字iは会場周辺の各駅を表しており,i=1は信濃町駅,i=2は国立競技場駅,i=3は千駄ケ谷駅,i=4は外苑前駅,i=5は青山一丁目駅を意味する.評価関数の値fが大きいほど,各地の混雑している状態を指す.また,混雑解消時間とは,人口が一定値を超え再び一定値以下となった時間と定義している.
式(1)は多目的最適化問題を表しており,右辺第1項で駅のピーク人口の最小化を図る評価関数を,第二項で駅の混雑解消時間の最小化を図る評価関数を設定している.多目的最適化問題では,すべての目的関数を同時に最小にする解は一般には存在しないため,ある成分目的関数を減少させても他の成分目的関数が増加しない,パレート最適曲面上の解のうち,意思決定者の目的に適った解である選好解を採用する[17].どの選好解を選択すべきか,式(1)のような加重和最小化問題の場合は如何に重みを決定するかといった選好最適化問題の解法として,意思決定者との対話を通して求める対話型Frank-Wolfe法や対話形だ円体法が提案されている[17].本稿では,選好最適化問題に関する言及は今後の課題として,各目的関数の重みであるk1とk2は所与のものとして扱う.なお,式(1)の評価関数は混雑を低減することを目的とするため,k1およびk2は正の値を取る.
4. 評価実験
4.1 シミュレータの精度評価
まず,構築したシミュレータが現実をどの程度再現できているのか確認する.実績として得られたデータは,イベント開始時刻15時,流出速度レベル5に相当するデータであるため,同一条件でシミュレーションした結果を表1に示す.ピーク人口相対値は,各駅の人口最大値について実績値を100としたときのシミュレーション結果の相対値を表している.
Table 1 Simulation accuracy based on maximum population of each station.
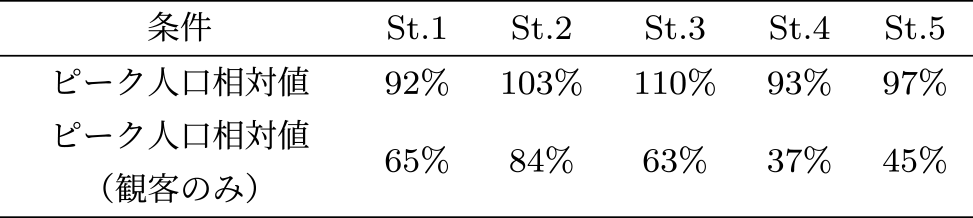
また,本稿の提案である観客以外の鉄道利用者をシミュレーションに含めることの有効性を確認するため,観客のみでシミュレーションした場合の結果を表1にピーク人口相対値(観客のみ)として示した.
表1のピーク人口相対値の結果より,駅同士でばらつきはあるものの,混雑ピーク値という観点ではおおむね1割前後の誤差で現実を再現していることが確認された.一方,ピーク人口相対値(観客のみ)の結果では,観客のみのシミュレーション結果では実績の人口から大きく乖離していることが確認された.
したがって,駅の混雑を検証するうえでは観客以外の鉄道利用者も含めて検討する必要があると考えられる.なお,St.2は比較的実績値に近い人口となっているが,この理由として,St.2である国立競技場駅は,一日平均乗降人員が大江戸線の中で2番目に少なく,当駅の利用者は国立競技場の観客が多くを占めることから[18],非観客の鉄道利用者を除いたシミュレーションを行っても,他の周辺駅程の違いはみられなかったと考えられる.
4.2 評価実験結果および考察
本節では,各条件におけるシミュレーションの結果を述べる.まず,式(1)の変数であるPiおよびTiの結果を示し,次に非観客×鉄道利用者エージェントの各駅の利用者数,そして評価関数の値fの結果について述べる.
PiおよびTiの結果を表2と表3に示す.表2と表3の値は,会場に最も近い駅であるSt. 2における人口ピーク値P2および混雑解消時間T2について,15時イベント開始,流出速度レベル5を100%としたときの比率である.
Table 2 Relative value of peak population of St. 2.

Table 3 Relative value of time taken to dissipate congestion at St. 2.

表2に示すように,流出速度レベルが大きくなると,つまり単位時間あたりの退場者数が多くなると,St. 2のピーク人口も増加している.一方,表3からは,流出速度レベルが高くなるにつれて,St. 2の混雑解消時間が短くなることが分かる.この結果は,流出速度を低くすると,ピーク人口は減少するが,慢性的な混雑が発生することを示している.なお,本稿でk1=k2として式(1)のfを求める.実際のイベントで適用するには,各駅の改札やホームの収容人数を考慮して,収容人数が小さい場合は人口を大幅に抑える必要があるため,k1/k2が大きなるように設定するといったことが考えられる.
次に,非観客×鉄道利用者エージェントの各駅の利用者数を示す.各駅における非観客×鉄道利用者エージェントの人口推移を図7に示す.図7は,各時間帯における観客を除いた各駅の人口を20分単位で集計し,最も非観客の多いSt. 5の人口最大値で除算した値(人口相対値)である.
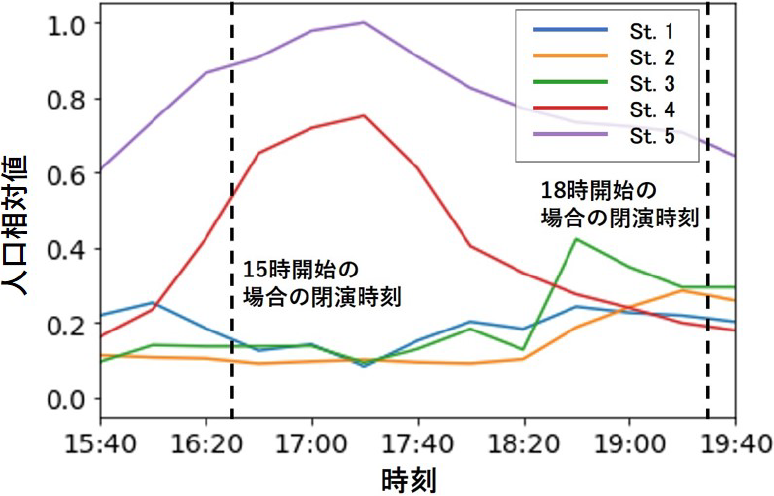
Fig. 7 Time series trends in relative population of non-spectator train users at each station.
St. 1, 2, 3については,18:30以降の利用が多くなる一方で,St. 4,5は17時台にピークを持つことが分かる.このように,近隣の駅同士でも鉄道需要の傾向には違いがみられることが確認できる.
最後に,評価関数の値fの結果について述べる.各イベント開始時刻における流出速度レベルに対する(1)の評価関数の値を図8に示す.15時イベント開始と18時イベント開始の場合では,評価関数の値の大きさやグラフ形状が異なることが確認できる.
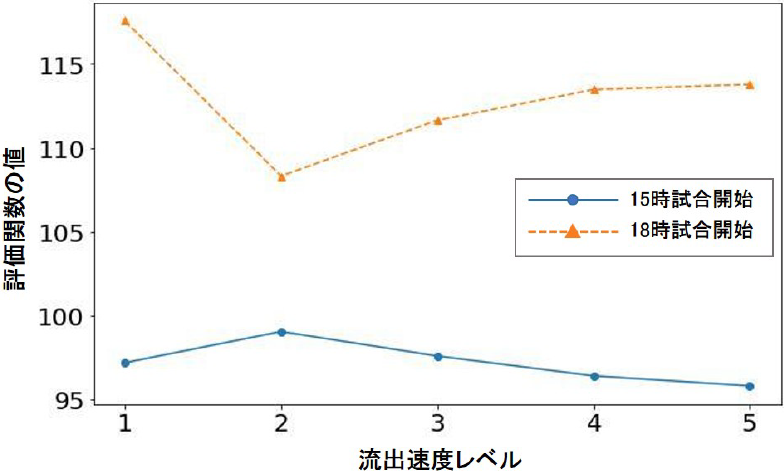
Fig. 8 Value of evaluation function.
15時イベント開始のグラフに着目すると,流出速度レベルが5の場合,つまり観客の退場をあまり分散させない場合,評価関数の値は最も低くなり,混雑を軽減できることを表している.一方で,18時イベント開始のグラフでは,流出速度レベルが2のときが,評価関数の値は最小となる.つまり,15時開始の場合には流出速度を大きく,18時開始の場合には流出速度を小さくすることが望ましいことを示している.図7によると,「15時開始の終了時刻」と「18時開始の終了時刻」では後者の方がSt. 1, 2, 3の非観客の利用者が多い.なお,図1に示すとおりSt. 1, 2, 3は会場に近いため,多くの観客が利用する.そのため,非観客と需要が重なる18時開始の場合は,流出速度を制限すべきだという直感にも沿う結果を得られた.
このように,時間帯に応じて非観客の鉄道需要が変化し,分散退場における流出速度の最適値は異なることが分かる.本検証によって,携帯電話基地局のネットワークデータから得られる位置情報とMASを用いることで,分散退場における流出速度の決定に対する示唆を得ることができた.
5. 得られた知見
本章では,シミュレーションの実施にあたり試行錯誤した観点を述べる.
5.1 観客の判定方法
3.3.2において観客の判定方法を述べたが,このロジックの設計にあたり工夫を要した.最初に検討した観客の判定方法は,イベントの開催中に会場内のIMCSに接続した履歴のあるユーザを観客と判定するというものであった.しかし,その方法で観客を判定した結果,会場の収容人数よりも過大な数値となった.この原因として,図3に示すように,イベントの開催中に偶然会場の周辺を通行した非観客を観客と誤判定している可能性を検討した.IMCSは施設内に向けて電波を発信するが,地上施設である以上,屋外に電波が漏れるケースがあるためである.
そこで,図4に示した判定方法を用いて観客を推定した結果,ユーザのサンプル規模を考慮すると会場の収容人数と同等な水準となったため,この方法で観客の判定を実施した.
5.2 エージェントの歩行速度の設定
エージェントの歩行速度は正規分布に従うようにシミュレーションを行ったが,その平均値と標準偏差の設定に試行錯誤を要した.歩道が混雑する場合,自由歩行の速度よりも歩行速度は落ちると考えられる[19].また,携帯電話基地局のネットワークデータは基地局単位のデータであるため,歩行速度を把握できる水準の時間粒度と位置粒度の情報を取得することは出来ない.
そこで,歩行速度の平均値について複数のパターンでシミュレーションを行い,会場の最寄駅である国立競技場駅の人口について実測結果とシミュレーションの結果の差が最も小さいものを採用することとした.平均値として{0.4, 0.8, 1.2} m/s,標準偏差0.2 m/sとして3パターンを検証した結果を表4に示す.表4より,実測結果とシミュレーションの結果の差が最小となった平均値0.8 m/sを採用した.
Table 4 Relationship between set walking speed and maximum population at Kokuritsu-kyogijo station.

今後別の会場にて同様の分析を行うにあたり,会場周辺の地理は同一ではないため,今回採用した値と同じものを採用できるとは限らない.そのため,別の会場についてシミュレーションを実施する際には,再び同様の探索を実施する,もしくは混雑時の歩行モデルを新たに組み込むといった実装が必要となる.
6. おわりに
本稿では,大規模イベントにおける混雑緩和策として注目される「分散退場」に焦点を当て,分散退場が会場周辺の駅混雑に及ぼす影響を試算するシミュレーションを構築した.携帯電話基地局のネットワークデータを利用し,観客と非観客の両方の動きをシミュレーションに取り入れた結果,観客の流出速度を調整することで,ピーク時の駅混雑を緩和する可能性が示唆された.また,混雑緩和のためには,イベントの終了時刻に応じた適切な流出速度の設定が重要であることも明らかになった.
本稿の意義は,従来の研究では困難であった,観客と非観客の両方の動きを考慮した混雑分析を可能にし,屋内外の位置情報データとMASを組み合わせて活用することで,分散退場の効果を定量的に示した点にある.社会情勢として,分散退場をはじめとする混雑緩和策の重要性が高まっている.特に昨今は,感染症対策の観点から,イベント会場や公共交通機関で密集を避けることが強く求められている.本稿で得られた知見は,混雑の緩和と安全の確保という社会的な課題の解決に寄与するものと期待される.
今後の課題としては,まずは実際のフィールドにて実験を行い,シミュレーションの妥当性を検証することが挙げられる.また,他のデータソースとの組み合わせやモデルの精緻化等によって,より現実に即したモデル化を行うことが求められる.たとえば,本稿では歩行速度は各道路の混雑状況によらず設定した正規分布に従うものとしたが,実際には道路や駅の混雑に応じて歩行速度が低下すると考えられるため,この現象をモデルに反映させる必要がある.さらに分散退場の効果は観客の流出速度だけではなく,事前の案内や誘導員の配置等も影響すると考えられるため,複合的な対策についても検討の余地がある.
将来的には,本稿で提案した手法を発展させ,オンラインでの混雑予測や動的な分散退場の実現等,より高度な混雑マネジメントへの応用が期待される.分散退場を実施する際の具体的な方策について,シミュレーションを活用しながら関係者との協議を重ね,実践的な示唆を得ることをめざしたい.混雑という社会課題は,イベント運営という枠を超えて,都市計画や交通政策とも密接に関連する課題である.本稿で得られた知見が,分野横断的な議論の促進と共創の契機となることを期待したい.
参考文献
- [1] 兵庫県警察:雑踏警備の手引き,〈https://www.police.pref.hyogo.lg.jp/zattou/index〉
- [2] 伊藤哲朗,牧野浩志,藤井 健,大口 敬:大規模イベント時の雑踏警備と安全な歩行者空間づくり,生産研究,Vol.73, No.5, pp.303–307(オンライン),DOI: 10.11188/seisankenkyu.73.303(2021).
- [3] Hagihara, G., Izumi, N., Yabe, T. and Mohri, Y.: イベント来場者の流れを変えるしくみ,IBS Annual Report研究活動報告(2019).
- [4] Zhonghua, W., Yongyan, W. and Yang, L.: Application of pedestrian simulation software in beijing olympic games a case study of olympic badminton venue, 2009 WRI World Congress on Software Engineering, Vol.2, IEEE, pp.254–261 (2009).
- [5] 丹羽 了,鷹見竣希,重中秀介,大西正輝,内藤 航,保高徹生:データ同化を用いた大規模イベントにおける分散退場の効果分析,IEICE Conferences Archives, The Institute of Electronics, Information and Communication Engineers(2022).
- [6] Chen, Q. and Crooks, A. T.: Delineating a'15-minute city' an agent-based modeling approach to estimate the size of local communities, Proceedings of the 4th ACM SIGSPATIAL international workshop on geospatial simulation, pp.29–37 (2021).
- [7] Henderson, L. F.: On the fluid mechanics of human crowd motion, Transportation research, Vol.8, No.6, pp.509–515 (1974).
- [8] Zheng, X., Zhong, T. and Liu, M.: Modeling crowd evacuation of a building based on seven methodological approaches, Building and environment, Vol.44, No.3, pp.437–445 (2009).
- [9] Jian, X.-X., Wong, S., Zhang, P., Choi, K., Li, H. and Zhang, X.: Perceived cost potential field cellular automata model with an aggregated force field for pedestrian dynamics, Transportation research part C: emerging technologies, Vol.42, pp.200–210 (2014).
- [10] Choi, M., Cho, S.-J. and Hwang, C. S.: Relieving bottlenecks during evacuations using IoT devices and agentbased simulation, Sustainability, Vol.13, No.16, p.9465 (2021).
- [11] Choi, M. and Hohl, A.: Investigating spatiotemporal indoor contact patterns using ABM and STKDE, Proceedings of the 4th ACM SIGSPATIAL International Workshop on GeoSpatial Simulation, pp.1–8 (2021).
- [12] 山下倫央,大西正輝:オリンピックにおける人の流れの解析,情報処理,Vol.55, No.11, pp.1189–1195(2014).
- [13] Grimm, V., Polhill, G. and Touza, J.: Documenting Social Simulation Models: The ODD Protocol as a Standard, pp.349–365, Springer International Publishing (2017).
- [14] Welcome to openstreetmap!, 〈https://www.openstreetmap.org/〉
- [15] Scenargie multi-agent extension module, 〈https://www.spacetimeeng.com/en/〉
- [16] H. Ohyane, D. Tanigawa, N. N. and Hiramoto, Y.: Base station supporting ip transport, NTT DoCoMo Technical Journal, Vol.9, No.1, pp.7–12 (2007).
- [17] 志水清孝:多目的最適化の理論と手法,電氣學會雜誌,Vol.103, No.7, pp.677–680(1983).
- [18] 各駅乗降人員一覧,〈https://www.kotsu.metro.tokyo.jp/subway/kanren/passengers.html〉
- [19] 内閣府 帰宅行動シミュレーションに係る参考資料(ケースごとの歩行速度分布図),〈https://www.bousai.go.jp/kaigirep/chuobou/senmon/shutohinan/pdf/case01.pdf〉

yuusuke.nakamura.xf@nttdocomo.com
2018年慶應義塾大学理工学部システムデザイン工学科卒業.2020年同大学大学院総合デザイン工学専攻前期博士課程修了.同年株式会社NTTドコモ入社.行動変容や人流分析,マルチエージェント・シミュレーションの研究開発に従事.

2014年東京大学大学院学際情報学府修士課程修了.同年株式会社NTTドコモ入社.2018年10月より東京大学大学院工学系研究科博士後期課程入学.人流データ分析に基づいた位置情報サービスに関する研究開発に従事.

2008年千葉大学大学院博士前期課程修了.同年,株式会社NTTドコモ入社.SNS,位置情報,ヘルスケアデータやスマートフォンログ解析,FinTech分野の研究開発に従事.2017年東京大学大学院工学系研究科博士後期課程修了.2020年8月より東京大学特任助教.博士(工学).情報処理学会,ACM,日本データベース学会各会員.

2008年株式会社NTTドコモ入社.以降,3G/LTE装置開発,位置情報技術開発,光ブロードバンドサービス開発,ビッグデータ分析に基づくサービス開発等に従事.2023年度情報処理学会業績賞受賞.

1998年東京工業大学工学部卒業,2000年東京工業大学大学院理工学研究科電子物理工学専攻修了.同年株式会社NTTドコモ入社.以降,無線LANシステム開発,3G/LTE装置開発,5G研究,3GPP標準化,IEEE802標準化,ARIB標準化,ビッグデータ分析に基づくサービス開発等に従事.2005年度電子情報通信学会学術奨励賞受賞,2023年度情報処理学会業績賞受賞.現在,日本電信電話株式会社.
採録日 2024年10月21日