1．はじめに

従来のパッケージングされて販売されるゲームと異なり，近年はアプリ形式のゲームやDLC（DownLoad Contents）の更新によって継続的に新たな遊びを提供するゲーム形態が一般的になってきている．しかし継続的な新しいアイテムやキャラクターなどのゲーム要素，ステージ課題やルールの追加・修正によって，ゲーム難易度などのゲームバランスが想定と異なる変化を起こしては本来の目的であるプレイヤーへの楽しさの提供にならない．ゲームの継続的更新が続く運営期間中，更新データ毎，リリース前に新要素追加後のゲームバランスを予測し，調整し続けることが重要であり，それをいかに行うかが現代のゲーム開発・運営における最大の課題の1つであるといえる．バランス調整のやり方はゲームごとにさまざまだが，ゲームの運営が継続すればするほど既存の要素との関係が複雑になり困難さが増していく．ゲーム性の複雑化による作業コストの増加，担当者の入れ替え時の知見共有の難しさ，バランス調整クオリティの定量化・画一化に対する指標の不在などは，程度の差こそあれゲームの種類によらずゲームバランス調整の普遍的な問題である．このような問題に対して，人工知能（機械学習） 技術を導入することは，ゲームバランスの予測検証と調整のために非常に有効であると思われる．本稿では，株式会社ディー・エヌ・エー（以下，DeNA） が提供する“逆転オセロニア”という対人戦がメインコンテンツであるゲームにおけるバランス調整への深層学習活用の試みを紹介する．ただし紹介する応用技術はまだ研究段階であり，運用に組み込まれたものではない．本稿の主題は“逆転オセロニア”のようにゲーム要素が非常に多く，更新されていくゲームへの実応用の際に発生した課題と，その対処に関する研究報告である．

2．“逆転オセロニア”の解説

本研究の導入を目指すサービスである“逆転オセロニア”（以下オセロニア）は DeNA がサービスを提供するスマートフォン向けアプリである. オセロニアは広く知られたボードゲームである“リバーシ”のルールでプレイするシンプルだが奥深い対戦ゲームで，プレイヤー2人でのPvP（Player versus Player）対戦がメインコンテンツになっている．

2.1　逆転オセロニアのルール

オセロニアの対戦ではリバーシと同様の設置ルールで，2人のプレイヤーは白駒，黒駒の持ち手に分かれ， 6×6 の盤面にそれぞれ1ターンに1つ駒を交互に置いていく．リバーシとオセロニアの最大の違いは使用される駒に固有の特徴があり，ある対戦で使用できる駒は自身の保有する中から事前に決めておかなければならないことが挙げられる．その駒の設置時に発生するダメージ・効果を駆使して相手の体力を先に削りきったプレイヤーが勝利するというのがオセロニアの対戦時の基本ルールになる. オセロニアにおける駒がどのような特徴を持つかなど，オセロニアで用いられる基本的な用語の意味を以下に示す．

駒（キャラクター駒）

オセロニアにおいて白または黒の駒（リバーシにおけるディスクの役割を担っている）にはそれぞれキャラクターが宿り，条件を満たすことで対戦相手や自分にダメージや，特殊な効果をもたらす．リバーシのルールによってほかの色に挟まれ，一度でも色を反転させられると駒に宿るキャラクターや継続的に発生している効果は消失する．駒には属性（神・魔・竜） が存在し，属性ごとに「神は耐久値が高め」，「魔はトリッキーな戦術向き」，「竜は攻撃力が高め」という傾向が存在する^☆1. 特に断りがない場合，本文中で使われる駒という用語はこのキャラクター駒のことを意味する．

デッキ

任意の16枚の駒によって構成されるプレイヤーが対戦時に使用する駒の集合を“デッキ”と呼ぶ．この組合せ次第で対戦時の戦略が変化するため，自身の得意な戦略などをあらかじめ想定して，デッキを組むこともプレイヤーの楽しみ，力量の見せ所の1つになる．また，この組合せにはプレイヤー間で流行があり，流行戦術を考慮して強力な駒をどう組み入れるかも重要な要素となる．駒にはそれぞれコストが設定されており，デッキ内の16枚の駒のコストの総計がある上限を超えないようデッキを組まなければならない．そのため強力な駒ばかりでデッキを構築することはできない．また，デッキの内容は後述するリーダー駒以外，盤面に置くまで対戦相手に開示されない^☆2．

手駒

自分の手番で，そのターンに盤面へ設置可能な駒の集合のことで，最大4枚．対戦開始時にランダムに自分のデッキから4枚の駒が手駒として与えられる．（パスが発生しない限り）1ターンに1枚を盤面に設置して消費し，次の自分のターンの開始時にデッキの残りの駒からランダムに供給される．また，手駒に関してもデッキと同様，盤面に置くまで何を持っているかは対戦相手に開示されない．

リーダー駒

デッキの中には必ず16駒の中から“リーダー駒”を設定しなければならない．リーダー駒のみ対戦相手に開示されてしまうため，そこから対戦相手にデッキ構成を推定されるリスクがある．その代わり，対戦開始時に与えられる4枚の手駒の中には必ずリーダー駒が含まれるため，手駒が配られる際のランダム性による戦術の不確実性を緩和することができる．

HPと勝利条件

それぞれのデッキのキャラクター駒の持つ個別の HP（Hit Point）というステータスの総計がプレイヤーの体力（以下，このプレイヤーの体力の方を HP と呼称）となる．キャラクター駒を盤面に設置する際や特殊効果の発動など，ゲーム中のダメージによりお互い HP を削りあい，先に相手の HP を削りきった方が対戦の勝利者となる．盤面を自身の色の駒で埋めることが目的でないことが通常のリバーシの勝敗ルールと大きく異なる点である．プレイヤーどちらかのデッキが尽きて残りの手駒も使い切ったときに，お互いの HP を削りきれていなかった場合，体力が多い方が勝利する．また HP を削り切る前に，盤面上の駒が一方の色のみになってしまった場合，リバーシと同様その色のプレイヤーが勝利者となる．

スキル，コンボスキル（特殊効果）

キャラクター駒の設置時に発生する基本ダメージのほかにも，「〇枚ひっくり返したとき」などの条件を満たすことによって駒固有に設定された特殊な追加効果が発生する．特殊効果は自身の HP を回復したり，数ターンの間，ターンごとに継続的なダメージを与えるなど，さまざまな種類が存在する．その駒の設置時に発生する特殊効果を“スキル”，すでに盤面に存在する駒がそのターンに設置された駒と連携して発生する特殊効果を“コンボスキル”と呼び，キャラクター駒はこのスキルとコンボスキルを最大1つずつ有している．このスキルとコンボスキルをうまく発動し，狙い通り運用することがプレイヤーに求められる基本的な対戦戦術になる．

囲碁や将棋の対戦時にかかるターン数に比べて，オセロニアは長くても32ターン（パスを含まない） で終わる手軽なゲームである．以上のように，オセロニアの対戦ではキャラクター駒の持つ特殊効果をうまく扱い，またそれを効果的に発揮できるデッキを構成することが重要となる．ただし場合によっては，流行する戦術・デッキに対処するために初心者からは一見すると効率的でない駒を使うこともあり，1つだけでなく，状況に応じた複数のデッキを編成する必要もあるなど，奥深い要素となっている．キャラクター駒の種類は2019年1月までで約3,000キャラクター存在し，継続的に追加リリースされている. 個々の駒のスキルなど，より詳細なルールは参考サイト[1], [2]に記載されている．

3．オセロニアにおけるゲームバランス

オセロニアに限らず PvP の対戦ゲームのゲームバランスとは，プレイヤーのプレイ戦術以外の何らかの要素で勝敗に大きな偏りを産んでしまわないかが重要になる．たとえば，将棋のようなターン制ゲームで後攻が必ず勝つ戦術が容易に見つかる場合，それはゲームバランスが崩壊しているといえる^☆3．ナッシュ均衡解が容易に見つかる簡単な零和ゲーム^☆4と異なり，将棋や囲碁などのナッシュ均衡解が見つかっていない複雑なゲームでは，初期状態（先攻・後攻）のみからでは勝敗は分からない^☆5．しかしこれらのゲームとは異なり，近年の対戦ゲームではプレイヤーの対戦開始時に有している初期条件（先攻・後攻以外の要素）が互いに異なる場合が多い．オセロニアであればこの初期条件にデッキの内容が該当する．

3.1　デッキ構築と戦略性

オセロニアにおいて，どのようなデッキを使用するかはプレイヤーがどのキャラクター駒を持っているか，どんな戦術を想定して事前に組み立てるかに依存する．特に保有している駒は明確な差となり，自分の思い描く戦術に沿ったキャラクター駒の入手や育成という対戦外の要素が勝敗に大きく影響する．一方で，多種多様な敵の戦略を相手取ることを想定して，欲しい駒を入手し，どのようなデッキを構築するか試行錯誤するのもオセロニアの楽しみ方の1つである．またデッキはその組合せにより，対戦相手として有利な組合せ，不利な組合せがある．そのため，あるデッキAではあるデッキBにどうしても勝てないという事例があったとしても，必ずしもそれだけでゲームバランスが崩壊しているとはいえない．そのような相性を理解してデッキを運用するのも戦略の1つである．

チェスや将棋など，最初から持ち駒の種類が固定された上での“戦術の研究の深淵さ”も対戦ゲームの楽しさの1つだと考えられるが，オセロニアをはじめとした近年の対戦ゲームの“ゲームの初期条件の構築の試行錯誤”や“対戦環境におけるその流行構築の変化への追従的な対応”も近代型のゲームの楽しみ方の1つであるといえる．

3.2　ゲームバランスの崩壊と新規駒

たとえばここで「ある一種の駒Aが強力すぎて，駒Aがデッキに入っているか否かでプレイヤーのプレイスキルによらず勝敗を決してしまう」場合を想定する．すると対戦環境では，自ずとその駒Aが入ったデッキが主流となり，デッキのバリエーションも少なくなる．そのような限られた状況下で自身の戦術を磨くのは，囲碁や将棋のような“戦術の研究の深淵さ”に該当するものの，多種多様な戦術のデッキと戦うこともオセロニアの楽しみの1つであるとすれば，この対戦環境の固着化はゲームバランスの崩壊だと言える．また，対戦に勝つために必須なある駒Aがゲーム運営中の“ある期間”にしか手に入らないのだとしたら，新しくゲームを始めるプレイヤーにとって非常に大きな不公平になる．これは極端な例であるが，さまざまなゲームで上記ほど極端でなくとも類似したゲームバランスの崩壊が発生する危険性を有している．

オセロニアでは定期的に従来と異なる能力やステータスを持つ新規のキャラクター駒がリリースされる．これがプレイヤー間の対戦環境の戦術の流行を動的に変化させていく．そしてある期間にのみ入手可能な駒も存在する．このような新規駒のリリースは戦術のバリエーションを増やし，環境の固着化を防ぐことで，新規・継続プレイヤー関係なく手軽に遊べるゲーム環境を提供している．一方で新規駒の導入を行うと，ゲーム全体としては理論的にそれまでと異なるゲームになる．そのため従来では考えられなかった，前述の例ほど極端でないにしろ対戦環境に流行するデッキを固着化させてしまう危険性を含んでいる．このような新たな特殊効果やステータスを持つ新規駒の導入が，事前に想定しない対戦環境のバランス崩壊を引き起こさないよう，慎重に新規駒の設計・調整を行うのがゲームバランス調整の役割である．

3.3　オセロニアにおけるゲームバランス調整の困難さとAI活用の意義

現在，オセロニアではバランス調整を専門としたプランナーが実際にリリース予定の新規駒についてさまざまなデッキに投入した際に想定外の強さを持たないかを検証している．バランス調整は圧倒的な対戦回数で習得したバランス感覚に基づき行われる．実際にはプランナー間の議論や，検証対象の新規駒を組み込んだ概ね対戦環境を網羅し得る，多様だが検証可能な数のデッキ構成での対戦を通して，バランスを調整していく．しかしながら，逆転オセロニアの駒は数千種類存在しており，類似した駒やデッキ構成を無視したとしても，その組合せは膨大になる．そのため，それらすべての駒の組合せを考慮するのは現実的に不可能である．また，バランス調整プランナーに必要な大量の対人戦によるバランス感覚の習得も高コストであり，どうしてもその調整能力は属人化してしまう．さらにいえば本来，非常に狭い特定の状況で起きるゲームバランスを崩壊させるデッキ，戦術の発見は，大量のプレイヤーが大量の対戦を行うことで発見される集合知の成果である．バランス調整をする側にはそのような集合知によって発見される知見を，少人数の労力で短期間に発見する高度な能力が求められる．逆にいえば，バランス崩壊の予見は“ある程度以上の賢いプレイ戦術”を有したプレイヤーによる膨大なパターンで大量の対戦を行い，確率的に発見することを期待することもできる．そのような数的に巨大なスケールでの対戦の実施は，疲労しない計算機・人工知能に適した業務といえる．そこで問題になるのは“ある程度以上の賢いプレイ戦術”を人工知能に習得させる方法である．

4．ある程度以上の賢いゲームのプレイ戦術を学習する既存の人工知能技術

機械学習を用いたゲームプレイの学習技術は近年目覚ましい発展を遂げている．まず，深層学習技術の発展と強化学習との融合により，レトロなビデオゲームにおいて，事前知識なしでゲーム画面から人間と同水準の成績を得られる行動方策の学習が可能になった[3] . 他方，囲碁は非常に取り得る状態数が多く，さまざまな戦略を相手取るため，人工知能が人間に対戦で勝利するのは困難と考えられていた．しかし近年，ゲーム木探索，深層学習，強化学習の知見の融合により人間のプロプレイヤーに勝る強さをAIプレイヤーが示し，チェスや将棋などの二人零和完全情報ゲームへ転用可能なアルゴリズムとして発表されている[4].

4.1　学習ゲーム課題としての逆転オセロニア

前述の通り，人工知能技術は深層学習と強化学習やゲーム木探索との融合により，従来不可能だったゲームプレイの学習を可能とした．他方，既存のゲーム課題での強化学習における行動の学習には，深層ニューラルネットワークなどによる関数近似が用いられるが，多くの場合，出力はあらかじめ固定の行動種類数で学習される. しかし現在の一般に頒布されている最新ゲームにおいては，前述の通りゲーム内容がオンラインに更新されていき，入力情報や出力行動数が増加するなど，レトロなビデオゲームにはない性質を持つ．これは入出力の増加に応じて学習ネットワークも指数的に巨大化するため，更新が継続的に続いていくと学習が困難なネットワークサイズになることを意味している．このように現代のゲームで深層強化学習を行うためには，増加していく入出力サイズを前提とし，それに対処する必要がある．たとえば，学習課題と見なしたときのオセロニアは以下の特徴を有する.

• （1）二人零和不完全情報ゲーム（本研究では課題の簡略化のため完全情報に変更）
• （2）ターン制かつ1ターンにつき1回の行動選択
• （3）可能な行動の集合が現在の手駒，場の駒配置で決定
• （4）潜在的な行動選択肢数は駒種類数×マス数（6×6）であり，駒種類数の増加によって増えていく可能性がある
• （5）駒が盤面にとどまるため，すべての駒を離散的に定義すると，駒の種類数の増加に対して指数的に状態空間が拡張される
• （6）手駒としての駒の出現順番が確率的で予測不能なため，ゲーム木探索が有効ではない
• （7）デッキの組合せが数多くあるため，すべてに対応としようとする場合は膨大なパターンへのマルチタスク学習になる

5．研究目的：オセロニアにおける戦術AIを作る困難の解決

オセロニアでは入力情報でありながら行動としての出力でもある駒の種類数がゲームの更新のたびに増え続けていく．そのため人工知能のアーキテクチャはその増加を前提に設計する必要がある．クラスタリングにより膨大な数の入出力を抽象化する手法は存在するが，ゲーム進行上のそれぞれの駒の特徴や役割は複雑かつ自明ではないため，有効とは限らない. また，人手による個々の駒の特徴量のハンドエンジニアリングも頻繁にゲームが更新されるため，現実的ではない．

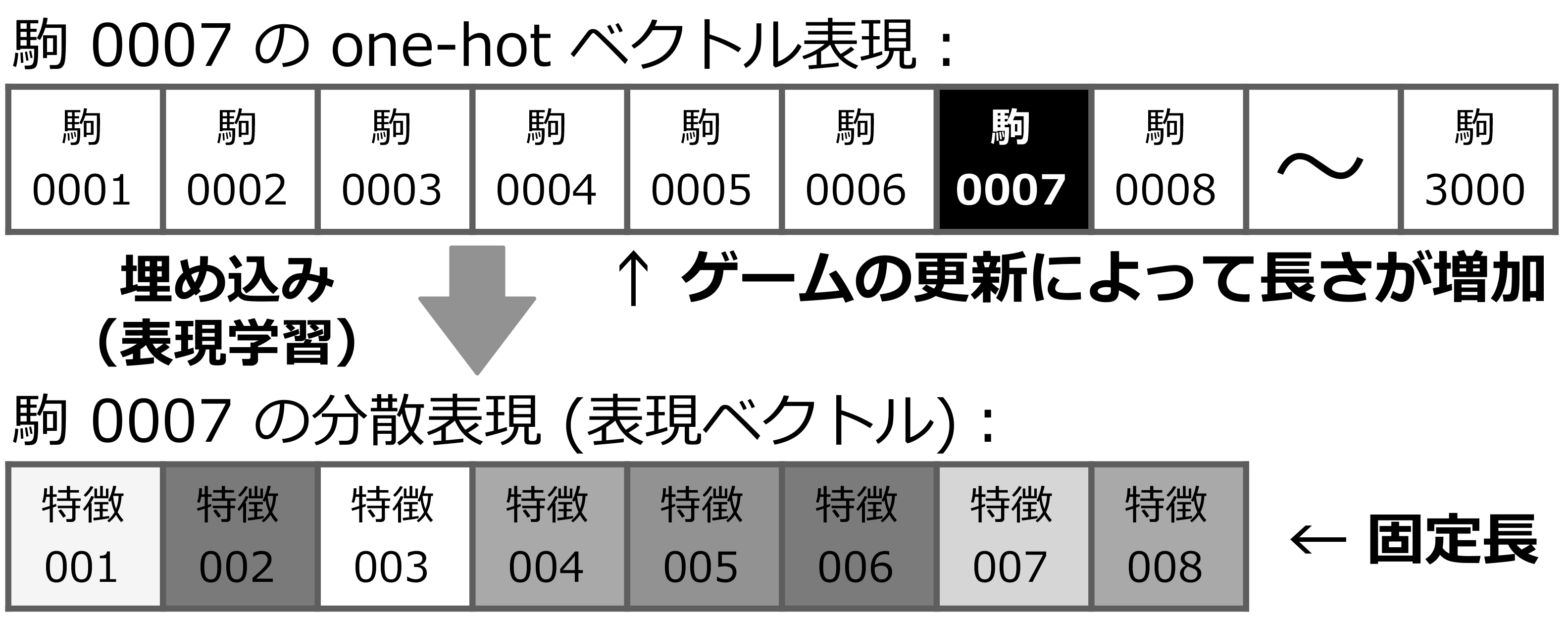
そこで本研究では，状態・行動両方の要素である駒の特徴を状態遷移軌跡^☆6から自動的に分散表現としてベクトルに埋め込む表現学習手法を提案する. 後述する提案手法は膨大かつ拡張されうる駒の種類数の長さを持つ one-hot ベクトルを，固定次元の実数ベクトル（表現ベクトル） に変換する（図1）．こうすることでプレイ戦術を学習する際のネットワークのサイズが駒の種類数に依存しなくなり，継続的な拡張に対処可能になる. この手法は逆転オセロニアに限らず，ゲーム要素が継続的に追加されるさまざまなゲームに有効であると考えられる．

6．プレイ戦術の学習

現在のゲーム状況に応じて適した行動を選ぶ人工知能を知能エージェントと呼ぶ（以下，断りがない場合，単にエージェントと記載する）．エージェントは特定の評価関数や確率分布に基づき行動する．評価関数は人間が試行錯誤を元に数値化して設計することもできるが，ゲームが複雑になるほど良い評価関数を与えることは困難になる．その評価関数を何らかの手法で学習・自動獲得させることが深層学習の役割である．深層学習には膨大なデータが必要であるため，サービス向上のためにプレイヤーの対戦ログを収集しているオセロニアのようなオンラインゲームと相性が良い．その対戦ログから人間の選択を教師信号として教師あり学習（Supervised Learning，SL）を行うことで，人間の選択を模倣する評価関数を獲得することができる．教師あり学習で学習したエージェントも，本研究が目的とするリリース予定の新規駒のバランス調整にはある程度有効だと考えられる．しかしながら，それはバランス調整対象の駒がそれ以前の駒に類似している場合に限られ，まったく新しいスキル，ゲーム要素の追加に際してはデータのない未知の状況からの学習が必要になる．そこで重要になるのが，未知の環境から試行錯誤を通じてゼロから良い行動パターン（価値関数，行動選択確率分布＝方策）を学習していく，強化学習（Reinforcement Learning，RL）という手法である．近年の研究では囲碁において深層強化学習で学習した方が対戦ログからの深層学習より高い成績を有することが示されている[4]．しかしここで前述の，オセロニアを始めとしたオンラインゲームが有する，ゲーム要素が追加されていく性質が深層ニューラルネットワークで行う教師あり学習，強化学習の両方にとって大きな問題になる．

6.1　駒の種類数の増加と学習の困難さ

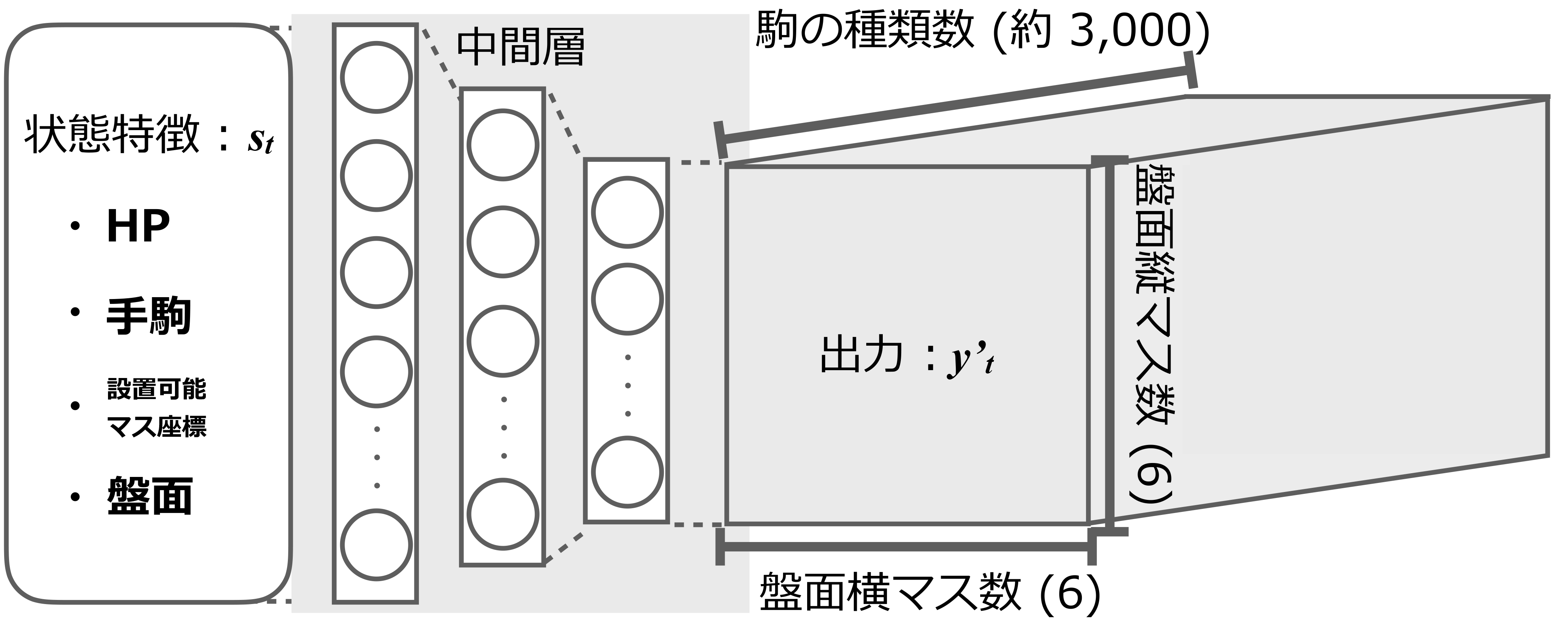
オセロニアにおけるネットワークの入力ベクトルは， 6×6 の盤面上の“どのマス”に“どの駒”が存在するかの情報が，サイズの大半を占める（ほかにも HP などのステータス状況，ゲーム特性に基づき設計された特徴量などが付随する）．この“どの駒”の情報のサイズは駒の種類数に依存するので，盤面情報のサイズは最低でも 6×6× 駒種類数になり，駒の種類が増えるほどにこのサイズは増大する．実際の入力時には盤面情報以外にも自分や敵の HP や手駒，デッキなどの情報を含む．手駒やデッキの入力特徴も1つひとつの要素は駒なので，盤面情報以外も駒の種類数に比例して入力ベクトルの長さが増えていく．また，駒は行動の選択単位でもあるため，実際に選択できるのは手駒にある4つの駒のみだが，潜在的にはすべての駒について評価値を出力できるようエージェントのアーキテクチャを設計する必要がある．これを DQN（Deep Q Network）[3] で扱えるよう単純にニューラルネットワークで近似関数を設計すると行動の出力数も図2に示すように 6×6× 駒種類数という膨大な数になる上，駒の種類数はゲームの更新のたびに増大していく．もちろん，入出力ベクトルが増加に応じて隠れユニット数も含めたネットワークサイズも増大し，学習は困難になっていく．

この問題に対処するため，我々は2つの工夫を行った．1つは選択する駒を出力として扱うのではなく入力に加えて可変長行動に対処するアーキテクチャの採用，もう1つは駒の特徴ベクトルを別途事前学習して埋め込む表現学習を併用することで駒の表現ベクトルのサイズを固定する手法の考案である．これらにより，プレイ戦術を学習するネットワークサイズを駒の増加によらず固定できた．

7．出力数が駒の種類数に依存しない評価関数アーキテクチャ

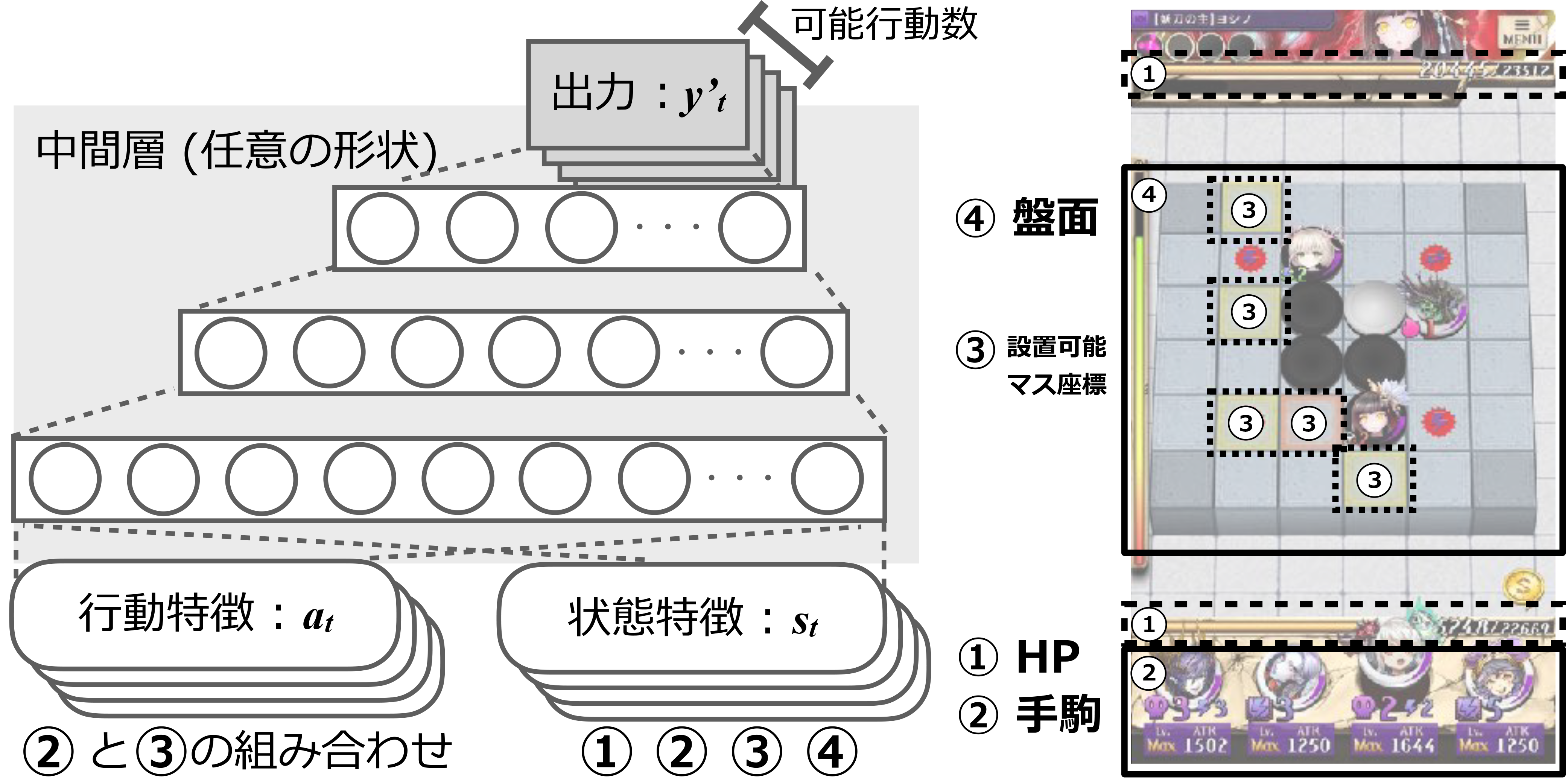
本研究においてエージェントはそのときに実行可能な行動集合の中から, 学習により付加した各々の行動評価値を参照して行動選択する. そしてある行動選択肢の評価値の計算・学習には近似関数を使用する. 近似関数には図3に示す状態特徴 $s$ ，行動特徴 $a$ を入力とし，スカラー値である評価 $y\text{'}=f\left(s,a;\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}\right)$ を出力とする多層ニューラルネットのアーキテクチャを使用した．こうすることで潜在的に可変長な駒の種類数に寄らず，常に出力を1つの行動に対する評価値のみにでき，アーキテクチャのサイズを縮小できる．また本アーキテクチャはターゲットとなる行動の評価関数 $y\text{'}$ の変更により，同様の入力形式に対する教師あり学習，強化学習のどちらにも用いることができる．

7.1　本アーキテクチャでの行動選択の方法

プレイ時の行動はある時点 $t$ での状態 $s_t$ において実行可能な行動集合 $A_t$ の要素をすべて評価し，その中で最も評価値の高い行動選択肢 $\mathrm{argmax}<!--\; \; -->{}_{a_i\in <!--\; \in \; -->A_{\mathrm{t }}}f(s_t,a_i;\mathrm{\theta <!--\; \theta \; -->})$ が選ばれる．ゲームプレイ時，1ターンの行動を決めるための行動評価時には，そのターン $t$ で実行可能な行動の長さ $\left|A_t\right|$ 分，そのターンの状態特徴をバッチ方向にコピーした状態特徴に，実行可能な各々の行動特徴を付加して行う．すなわち，本アーキテクチャでの行動選択では，学習時にはバッチ方向とされている出力 $\mathrm{tensor}$ の次元で各行動の評価値の計算が出力される．

7.2　本アーキテクチャに入力される行動の特徴ベクトル

本研究で行動の価値を近似する近似関数 $f\left(s,a;\mathrm{\theta \; <!--\; greek\; small\; letter\; theta\; -->}\right)$ に入力される行動特徴を定義する. 多くのビデオゲームにおける行動は，離散的に定義されたコントローラのスイッチ種類数に対応する on/off のバイナリベクトルで定義できる．本課題，カードゲーム要素を持つオセロニアでは手駒になくてもゲームに存在するすべての駒が，離散的に定義された（潜在的な） 行動選択肢に該当する．そのため駒の種類数の長さの one-hot ベクトルで行動特徴が定義される. オセロニアの場合，“どこに”駒を設置するかを意味する盤面空間 6×6 の one-hot 行列，各駒を当該の座標に置くことで効果（スキル・コンボスキル，詳細は参考サイト[1],[2] に示されている）が発動するかどうかの2値フラグ，その駒の元々の攻撃力なども行動特徴に該当する.

7.3　対戦ログからの教師あり学習

オセロニアではプレイヤーの対戦ログを用いて，実際にプレイヤーがどの局面（状態 $s$ ）で手駒中のどの駒を，設置可能なマス中のどの座標に設置したか意味する行動 $a$ の選択について教師あり学習を行うことができる．

本研究では，ある状態において選択可能な任意の行動が選ばれた $\mathrm{（put）}$ か否か $\mathrm{（not\; put）}$ の可能性 $p_{\mathrm{put}}(y\in <!--\; \in \; -->\{\text{put},\text{not put}\}|a,s)$ をプレイヤーの主観的な行動評価値として学習する. この定義により，入力である状態特徴 $s$ ，行動特徴 $a$ が実際に対戦ログ上で選ばれたか否かの2値分類タスクになるため，近似関数の出力 $y^{\mathrm{pred}}=f_{\mathrm{put}}\left(s,a;\theta \right)$ を対戦ログ上の教師信号 $y^{\log }$ に対する cross entropy 損失関数で学習可能になる. また2値分類であるため，手駒中の選択されなかった駒，設置可能だが選択されなかったマスも学習データに用いる. しかし毎ターン選択可能な行動の種類数 $\left|A_t\right|$ の中で選択されない行動数 $\left(\left|A_t\right|-1\right)$ の方が圧倒的に多いため，学習時には負例（選択されなかった行動の入力ベクトル）はダウンサンプリングしている．

7.4　ゲームシミュレータからの強化学習

本研究ではオセロニアのゲームシミュレータを用いて行動選択の強化学習も行った. 近似関数 $f(s,a;\mathrm{\theta <!--\; \theta \; -->})$ の近似対象として報酬 $r_t$ の累積値である収益の予測値である行動価値関数 $Q(s,a)$ を学習する. 本研究において行動価値関数の近似関数 $f_{\text{Q}}(s,a;\mathrm{\theta <!--\; \theta \; -->})$ は one-step buckup の off-policy なTD学習の更新則[5] にしたがって学習を行う．学習にはDoubleDQN [6] とCategorical DQN [6] を元に本アーキテクチャに沿った形のアルゴリズムを用いている．Categorical DQN とはあらかじめ決められた bin 数で区切られた Q 値の分布として近似関数を学習する方式[6] であり， Q 値の離散的な分布を学習している^☆7．ある時刻 $t$ に対する当該の状態行動対 $(s_t,a_t)$ については Categorical DQN における KL divergence 損失関数[6] を最小化するようPrioritized Experience Replay（PER）[7] を用いて学習した. ここで $A_t$ , $r_t=\{0,1\}$ はそれぞれ時刻 $t$ で実行可能な行動集合と得られた報酬を意味し，本課題で報酬はゲームの勝敗が決したときのみ与えられる（勝利時に $r_t=1$ ，敗北時に $r_t=0$ ）．

7.4.1　Categorical DQN と Noisy-net の変更

本アーキテクチャを用いた場合，DQN [3] などの手法と異なり，近似関数 $f_{\text{Q}}(s_t,a_t;\mathrm{\theta <!--\; \theta \; -->})$ の出力は常に1つのスカラー値である. 後述する本研究の学習実験では Categorical DQN を調整，変更したアルゴリズムを用いているため，分布を bin 数で区切った出力の各 bin 範囲に対する期待値を Q 値として用いている．出力分布の範囲は報酬のスケールと同じく[0, 1] としている^☆8．Categorical DQN における近似関数 $f_{\text{Q}}(s_t,a_t;\mathrm{\theta <!--\; \theta \; -->})$ の更新アルゴリズム（Categorical RL algorithm）に用いる Target-net $f_{\text{Q}}^{\text{target}}(s_t,a_t;{\mathrm{\theta <!--\; \theta \; -->}}^{-<!--\; -\; -->})$ のパラメータ ${\mathrm{\theta <!--\; \theta \; -->}}^{-<!--\; -\; -->}$ は以前の近似関数 $f_{\text{Q}}$ のパラメータ$\mathrm{\theta <!--\; \theta \; -->}$としている．これは一定間隔の間 ${\mathrm{\theta <!--\; \theta \; -->}}^{-<!--\; -\; -->}$ を固定することで関数の更新を安定させている深層強化学習の一般的な手法である[3] .

またネットワークには Noisy-net [6] を使用し，自律的な探索を促している．通常の Noisy-net [6] を本アーキテクチャで用いると，行動がバッチ方向に展開されている都合上，すべての行動に同様のノイズがかかってしまう．そこで本研究では，最終出力のみ，バッチ方向にそれぞれ異なるノイズが発生するよう，バッチ数分のノイズサンプリングをするよう設計した．

7.4.2　TD 誤差の計算過程の工夫

Double Q-Learning [8] を適用する際には次状態の Q 値ベクトルに対して argmax を演算する必要がある． One-step buckup の off-policy なTD学習の手続きとしては次状態の行動集合に対してバッチサイズ分 argmax を取ることになる．しかし本アーキテクチャでは次状態に紐づく行動数は可変長であり，かつバッチサイズ分の回数を各学習ステップごとに計算しては学習速度が大幅に遅くなる．そこで本研究では，すべてのバッチ数分，次状態の可変長の状態行動特徴数をバッチ方向に結合した可変長の長い minibatch に展開し，一括で Target-net へ入力，計算している．次状態のバッチ次元においてどこからどこまでが当該の状態に紐づく出力か展開時に覚えておけば，問題なく argmax が取れる．この形式はバッチサイズこそ大きくなるが行列計算として一括で行える利点を有している．バッチの結合と argmax を取る手続きが必要ではあるが，バッチサイズに対して個々に可変長の次状態のQ値を計算する必要がない分，計算速度は速くなる．この minibatch 一括展開の採用により，採用しなかった場合に比べて， tensorow 上で学習速度がおよそ4倍に速くなった^☆9．

8．駒の表現学習

本研究では自然言語処理分野で用いられる手法[9],[10],[11]を参考に，近似関数 $f(s,a;\mathrm{\theta <!--\; \theta \; -->})$ の入力であり，拡張され得る行動特徴 $a$ を固定長の実数ベクトル（表現ベクトル）として暗黙的に学習する手法を提案する. 具体的には話者特徴を表現ベクトルとして埋め込むペルソナモデル[10] を元に，状態行動対中の離散的な行動要素など，ある部分集合（オセロニアでは駒のことを指す）に，状態遷移の要因としての表現を表現ベクトルとして埋め込む方式を考案した.

8.1　学習方法

ある時点 $t$ での状態 $s_t$ と行動 $a_t$ , その次状態 $s_{t+1}$ が与えられたときを想定する．またそのときにネットワークに入力される状態行動対の特徴ベクトルを $X_t=\mathrm{\chi <!--\; \chi \; -->}(s_t,a_t)$ とする^☆10．ここで状態遷移軌跡 $(s_t,a_t,s_{t+1})$ が，特徴ベクトル $X_t$ 中でその個別の特徴量（特徴次元それぞれの値） の任意の部分集合 $x_t^{\text{tar}}$ を主原因として引き起こされたと考える．この任意の特徴量の部分集合を $x_t^{\text{tar}}$ を本研究では部分遷移要因と呼び， $X_t$ のそれ以外の特徴量 $x_t^{-<!--\; -\; -->}$ と表記することとする．オセロニアではそのターン使用された駒を識別する特徴^☆11が部分遷移要因 $x_t^{\text{tar}}$ に相当すると考えられる．そして状態行動対 $X_t$ から部分遷移要因 $x_t^{\text{tar}}$ をマスキング（当該の次元だけ値をすべて0に置換）された入力特徴ベクトル $X_t^{-}$ を定義する．このマスキングされた入力特徴ベクトル $X_t^{-}$ を用いて次状態 $s_{t+1}$ の予測を任意の予測器 $f_{\text{rep}}$ で学習すると，部分遷移要因 $x_t^{\text{tar}}$ によって引き起こされる状態遷移の予測に必要な勾配が行き場を失う. そこで入力としてマスキングされた入力信号 $X_t^{-}$ のほかに $x_t^{\text{tar}}$ に対応するランダムに初期化されたユニークな変数ベクトル $c_t^{\text{tar}}$ を与えて，次状態 $s_{t+1}$ の予測学習を行わせる. これを多くの状態行動対 $X$ に対して行うことで同様，あるいは類似したいくつかのマスキングされた入力 $X_t^{-}$ に，それぞれ異なる結果 $s_{t+1}$ が起きたとき，その差異の要因となる勾配が変数ベクトル $c_t^{\text{tar}}$ に吸収されて，部分遷移要因 $x_t^{\text{tar}}$ の状態遷移に寄与する表現が暗黙的に学習されていく. 部分遷移要因が行動要素（キャラクター駒）である場合は行動 $a_t$ の入力表現 $a_t^{\text{rep}}=c_t^{\text{tar}}$ ，あるいはその特徴ベクトルの一部に関する表現ベクトルとして行動方策の学習に再利用される．

学習に用いる状態行動対の特徴ベクトル $X_t$ と次状態 $s_{t+1}$ の状態遷移軌跡は環境モデル上でありえる遷移であればよい. しかし良い行動の評価関数を作るため，実用上は一定のリテラシーを持ったエージェント，あるいはプレイヤーの対戦ログから得た状態遷移軌跡が望ましい．

8.2　次状態の代替え特徴と損失関数

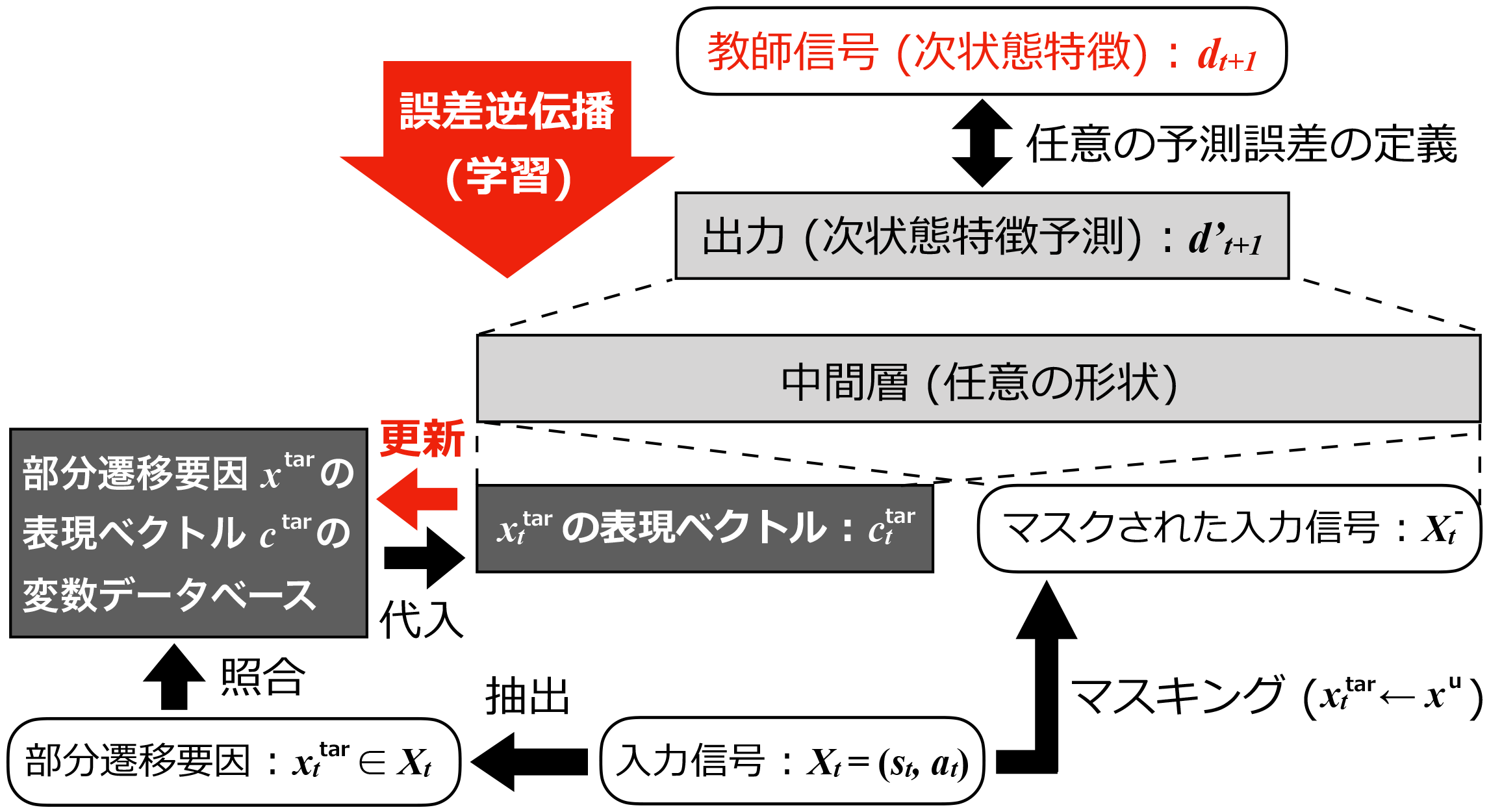
現実的には次状態 $s_{t+1}$ の直接的な予測は困難である. 特にオセロニアは行動特徴が手駒や盤面上の情報として状態特徴にも現れるため，長大で延長を前提とした駒種の one-hot ベクトルを含む $s_{t+1}$ の推定は不可能である. そこで十分に次状態 $s_{t+1}$ の代替えとなり得る，状態要素の部分集合や，行動 $a_t$ を実行した後に発生する観測可能な特徴を教師信号とすることも想定する. 次状態の特徴量そのもの，その代替え特徴も含めて本表現学習手法の教師信号を次状態特徴 $d_{t+1}$ と本研究では呼称する. この次状態特徴 $d_{t+1}$ とその損失関数の設計は次状態の予測の困難さや観測し得る特徴量などに依存するため，損失関数であれば連続量は正規化して回帰，排中律を有する離散事象の集合部のみ cross entropy にするなど，ゲームドメインごとに設計する必要がある. オセロニアではそのターンに発生したダメージや効果の種類などを代理の次状態特徴として，その予測誤差の伝搬によって表現ベクトルを学習している．以上の表現学習器の基本的なアーキテクチャを図4に示す．

代替え特徴量を使わない場合，たとえばビデオゲーム（画像・動画から） の行動選択の学習に本手法を用いることを想定する．その場合に次状態特徴 $d_{t+1}$ とされるのは，次状態である画面の各ピクセルごとの各要素の発生確率であり，予測誤差を最小化するように学習することで表現ベクトルが学習されると考えられる. しかしそれは現実的ではないため，何らかの別の特徴量を設計するのが妥当だと考えられる．

8.3　表現ベクトル導入の効果

表現ベクトルのネットワークの入出力を固定するのみでなく，ユニット数の節約と学習時間の削減や，表現空間上での類似行動の汎化による学習の効率化が期待できる．また，ほかにもプレイ戦術の学習器に駒の表現の学習を任せなくてもよいため，プレイ戦術に特化した学習のチューニングサイクルが早くなる利点があげられる．以降の実験でその利点の検証を行う．

9．プレイ戦術の学習実験

本研究では表現ベクトルの導入しても成績が保たれているか，また学習時間の削減ができているか検証するため，それぞれ表現学習と教師あり学習（実験1），強化学習による行動評価値の学習（実験2）を組み合わせた際の実験により定量評価を試みた.

9.1　逆転オセロニアでのプレイ戦術学習の共有設定

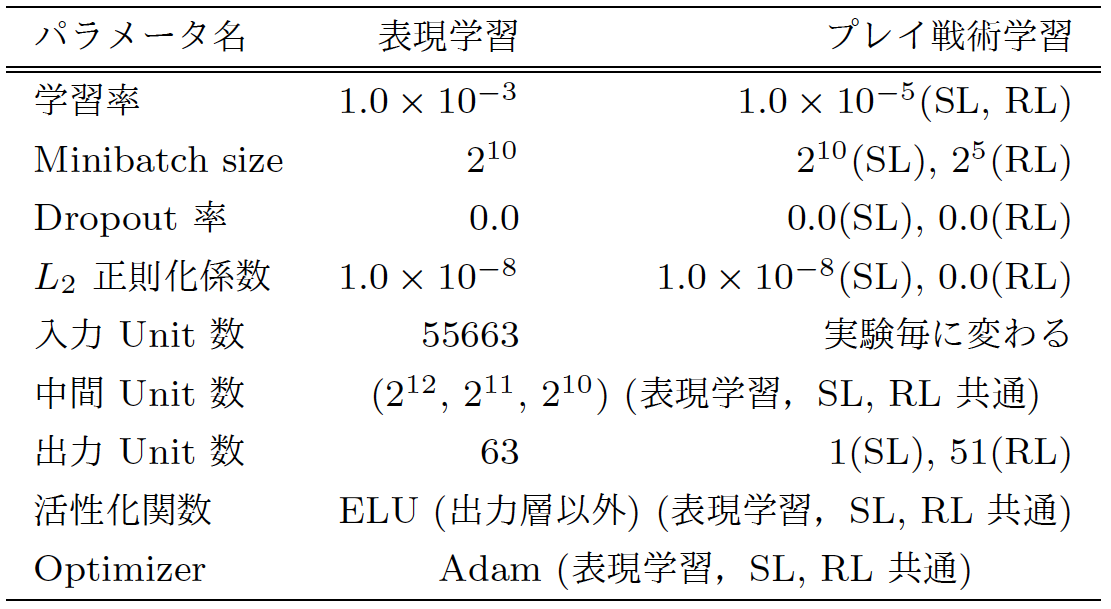
実験1, 2ともに状態・行動特徴の中に存在する駒特徴には共通の表現ベクトルを用いた. 駒の種類数そのものは2019年1月までで約3,000キャラクター存在する．本研究では2017年1月に使用できた約900種（+ キャラクターの付加されていない無地駒1種）のキャラクター駒を対象に学習を行った．具体的には全体で1～200^☆12のプレイヤーランクのうち上位のランクである76～200 同士の対人戦データから得られる状態遷移軌跡を用いて表現学習を行い，キャラクター駒の表現ベクトル（ベクトル長：30）を獲得した. また実験1の教師あり学習，実験2の強化学習には同様の中間層の構造を用いる. 各種学習器の構造やハイパーパラメータは表1に示す通りである. また Dropout ，L2 正則化の汎化は表現学習，教師あり学習のみにしか使用しておらず，強化学習には使用していない.

9.1.1　入力特徴

各学習器の入力特徴は状態 $s_t$ としてターン数や選択側の色（白・黒），自分・敵の残り体力，手駒，デッキ，盤面などを，行動 $a_t$ には任意の選択可能な駒や設置可能なマス座標，スキルやコンボスキルなどの特殊効果の発動の可否を用いた. 表現ベクトルを使用しない場合は one-hot ベクトルを手駒，デッキ，盤面の駒の表現として用い，駒の表現ベクトルを使用する場合は，そのすべてを前述したベクトル長30の表現ベクトルに置き換えた. そのため両実験とも比較対象である表現ベクトルを使うか否かで第一層の入力数とパラメータの数が異なる. ターン数を対数にした値など入力の特徴量エンジニアリングも行われているが，入力特徴や表現学習時の教師信号，損失関数は実サービスのゲームを用いている都合上，詳細な言及は避ける. 異なるゲームに本研究内容を応用する場合，ゲームごとに入力特徴を設計する必要がある．

9.1.2　勝率の定義

オセロニアでは非対人対戦イベントや通信が切れた際の代打ちとして，ルールベースAIが実装されている. ルールベースAIの行動はある得点表の合計値（評価関数）を参照し生成された確率分布によって選択される. 強さが固定であることと，決定論的な行動でないことから, 本研究の勝率の定義にはルールベースAIとの戦績を用いた. 勝率は各試合，各々異なるシードでデッキのシャッフルと先攻後攻を決定した1,000試合中何勝したかで評価した．勝率評価の試合時には学習された行動評価の近似関数の出力に対して greedy な行動選択を行った.

9.2　実験1：表現ベクトルを用いた対戦ログでの教師あり学習

実験1では表現ベクトルを用いた場合とそうでない場合での学習効率の比較を示す. ここでいう効率とは計算時間に対する勝率の向上速度や，最終的な到達勝率の高さを意味する. 勝率はさまざまなデッキの組み合わせによって測るべきだが，現実的にあらゆるデッキの組合せで評価するのは困難であるため，ここでは代表として2017年1月の時点でよく使われていたデッキバリエーションである4種を用いた．限定された駒種類数での勝率評価であるため，表現ベクトルの有無で大きな差が現れないことが予想される. そのため minibatch で学習した学習回数（step）に対する勝率以外に，同条件で学習にかかった経過時間を提示する．

9.2.1　実験設定

教師あり学習でも表現学習と同じく2017年1月に集計されたプレイヤーランクが76～200同士の対戦ログを使用した. 勝率評価に4種の内訳はデッキ内の駒の属性を神（耐久値が高い傾向），魔（戦術がトリッキーな傾向） ，竜（攻撃力が高い傾向）の駒で主に構成した3種とそのバランス的な組合せを用いた. 学習と評価に使用したデッキの構築はアソシエーション分析と階層的クラスタリング手法の一種であるウォード法と k-means 法を組合せたクラスタリングにより抽出した頻出する駒の組合せから [12]，任意の組合せによるデッキを自動生成した. プレイ戦術の学習ネットワークの表現ベクトルを使用する場合の入力サイズは5,649になった. それに対して表現ベクトルを使用しない場合，2017年1月時点で使用された駒種類数（約900種+無地駒1種） を直接扱えなければならないため74,570にもなり，表現ベクトルを使用した場合の約13倍となった. 前述の通り，実際にプレイヤーが選択した行動（正例）と選択しなかった行動（負例）の教師データ数の偏りが大きいため，正例と負例の割合が1:5になるようダウンサンプリングして学習を行っている（可能な行動の集合の数 $|A_t|$ が6より小さかった場合はのぞく）．すなわち，学習データの量はすべての対戦の総ターン数に対して約6倍になる．

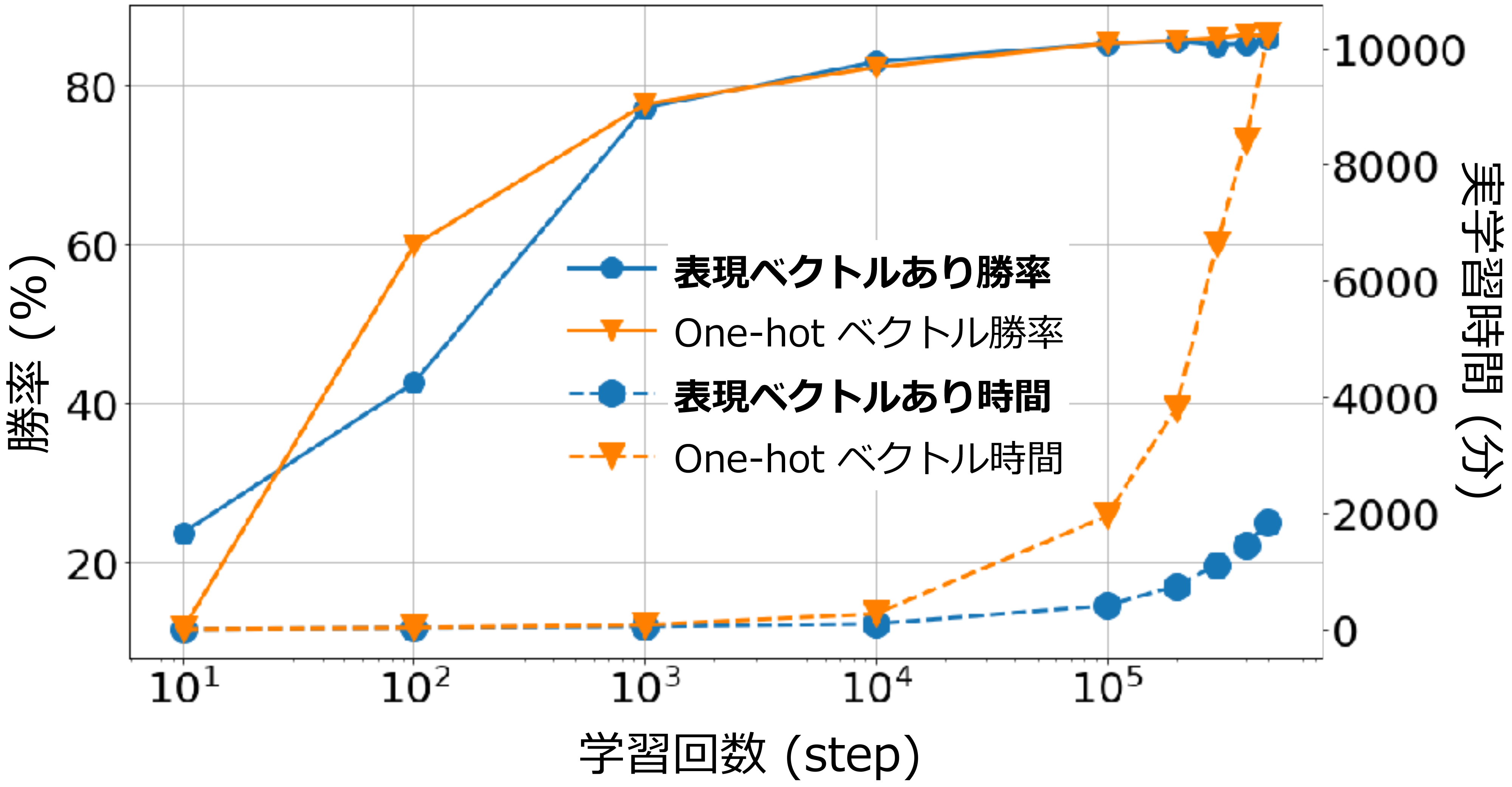
9.2.2　結果および考察

図5に各 step での勝率と，同条件の GPU で学習させた場合の経過時間を示す. 毎 step の勝率はほぼ等しいが，50万 step 時の経過時間が約5.6倍になった. これは約900の駒種類数を想定したものであり，学習コストは駒の増加に伴いさらに大きくなる. 本研究ではアソシエーション分析とクリスタリングにより生成されたメジャーなデッキ構成を用いたため，マイナーな駒の学習などに影響を評価できていないが，駒表現ベクトルが計算的な時間削減に寄与し，成績に影響を及ぼさない示唆が得られた.

9.3　実験2：表現ベクトルを用いたマルチタスク強化学習

強化学習でも表現ベクトルの使用に対して成績に変化が表れるか実験を行った. 教師あり学習と異なり，自・敵デッキは3種類のデッキに固定して強化学習を行った．つまり本実験課題は自・敵デッキで， 3×3 の9パターンの対戦を同時に学習するマルチタスク課題になる．3種類のデッキの内訳は，高火力で短期戦術が得意なデッキ（短期決戦型），毒ダメージや罠やカウンターなどの特殊戦術デッキ（搦め手型），回復など長期戦術が得意なデッキ（長期耐久型）である．3種のデッキに共通する駒は含まれていない．本実験に使ったデッキ構成はゲームタイトルへの影響を考慮して非公開にした．出力数は SL と異なり，Categorical RL algorithm を使用して任意の bin 数で区切られた分布として出力される．

9.3.1　実験設定

対戦相手には初期1,000対戦はランダムで，その後1,000対戦ごとに保存される過去の近似関数を対戦毎にランダムに読み込み，対戦相手の行動選択に用いた. アーキテクチャには表現ベクトルのあり, なしをぞれぞれ学習し，勝率を比較した. 実験1の教師あり学習と同じく，約900種 + 無地駒1種について事前に学習したベクトル長30であるため表現ベクトルを使用する場合の近似関数の入力サイズは5,649になった. 対して表現ベクトルを使用しない場合，駒16種 + 無地駒1種で計18の長さの one-hot ベクトルを使い，入力サイズは（16種しか使用しないゆえに）3,964になった. 学習は PER（Importance sampling のパラメータは $\mathrm{\alpha <!--\; \alpha \; -->}=0.7$ ， $\mathrm{\beta <!--\; \beta \; -->}=0.5$ ）により抽出された minibatch での学習を 1 step として2対戦ごとに 32 step 学習を繰り返し行った. このときに損失関数に用いる割引率 $\mathrm{\gamma <!--\; \gamma \; -->}=0.999$ で Replay Buffer のサイズは1ターンの状態行動対を1つの単位として2,000,000とし，Target-net パラメータ ${\mathrm{\theta <!--\; \theta \; -->}}^{-<!--\; -\; -->}$ は4,000 step の学習ごとに更新した．また，Categorical RLalgorithm での bin 数は51に設定した．自・敵のデッキは前述した3種類（短期決戦型デッキ，搦め手型デッキ，長期耐久型デッキ）からエピソード開始時にランダムに選択される．

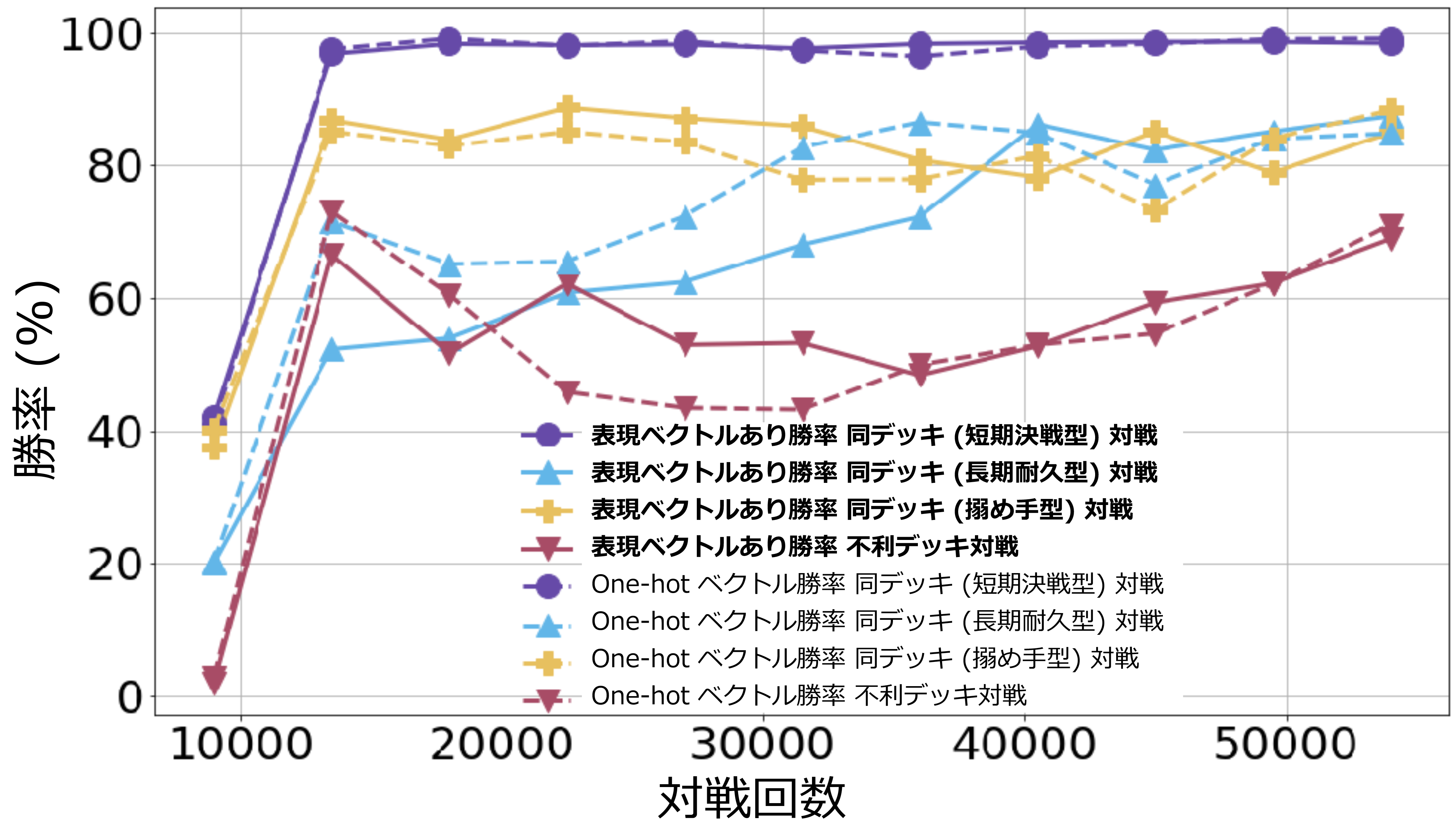
9.3.2　結果および考察

図6に対戦回数に対する勝率の推移を示す. 対戦回数ごとの勝率はほぼ等しく，強化学習でも表現ベクトルの使用により，成績に悪影響を及ぼさない示唆が得られた. 教師あり学習のときと同じく，駒の種類数が増えるほどネットワークサイズは大きくなる．本実験で表現ベクトルなしで学習が行えたのは，今回の実験が3種類のデッキ（3×16＝48 種類の駒）ゆえであり，教師あり学習と異なり学習のコストが高い強化学習では，数千種類の全キャラクター駒を扱うとなると現実的な時間での学習は不可能になる．その点でも表現ベクトルの有効性を示すことができる．

10．実応用を見据えた本研究の貢献

本研究の貢献はプレイ戦術の学習時に離散的なゲーム要素^☆13の種類数を制限なく扱える点にある. トレーディングカードゲームなど，離散化された状態や行動の要素数がトランプの枚数とは比較にならない数で存在する意思決定課題に対処するためには，そのゲームのドメインに基づいた個別要素の特徴付けが重要になる. それに対し，提案手法により事前に獲得した表現ベクトルを用いることで，拡張され得る膨大なゲーム要素に表現ベクトルの学習という形式で半自動的に“暗黙的な特徴”を与えられることを示した. それにより複雑なゲームへの機械学習，強化学習の応用範囲を広めることができたといえる. また，本研究はゲームルールが明示されている際に，スクロールやクリックなどの低次な行動の学習を無視し，一足飛びで高次な意思決定の学習を行えることを意味している. それは状態や選択肢の個別要素の特徴について，それらをハンドエンジニアリングで設計することだけでなく，それら特徴をアーキテクチャレベルの設計と事前学習を組み合わせて獲得することの有用性を示している．今後，過去の経験や知識に基づく“スキル”^☆14の汎化・活用のために機械学習を用いた行動の意思決定課題はますます複雑化していく. そのとき，低次の行動から高次行動（スキル，プラン）の発見と汎化が前提となることが予想される. そこでは本研究のように拡張され得る特徴空間を想定し，潜在的に膨大な行動の種類数に対して意思決定していける学習設計が重要になると考えられる. そのメタ設計，メタ構造はゲームジャンルに依存せず転用可能である．

11．今後に向けて

本研究の試みにより，最大の問題の1つである，継続的に増えていくゲーム要素を考慮した戦術の学習（教師あり学習，強化学習）を行うことができた．しかしながら，未知のゲーム要素を加えた環境下での膨大なデッキの組合せすべてに対して最適な戦術を学習するというマルチタスク強化学習への対処は未だ不十分である．強化学習は対戦ログのデータがなくとも未知の要素にも対応し得る教師あり学習にはない優れた性質を有する．しかし前述のマルチタスクなど，すべての問題に対処するのは現実的でない．ゲームバランス調整のような人間の複雑な仕事を補助するためにも，現代のゲームタイトルに強化学習を用いた際の問題の分解の仕方，その成果を共有していくことが今後の業界全体に対する貢献になると思われる．