Query-Adaptive Multidimensional Indexing on Scalable Data Stores

 今日，Eコマースにおける取引ログ，センサーデバイスによる計測値など，膨大なデータを収集・蓄積し，分析することが一般的になっている．これらのデータは，たとえば取引ログの場合は，いつ，どこで，だれが，何を購買したかなど，複数の属性からなる多次元データである．そして，これらの属性の範囲に対する集計・統計の問合せ処理（クエリ）が基本的な分析処理となる．

 このような分析処理時間の多くは，必要なデータの取得に費やされており，その高速化が実用上の課題である．また，これらのデータは増え続けるデータであるため，データ量に応じてシステムの規模を拡張する能力（スケーラビリティ）も不可欠である．そこで，本研究では，このような多次元データに対する基本的なデータ取得を効率的に行うことができ，かつ，スケーラビリティを備えた多次元索引手法を提案した．

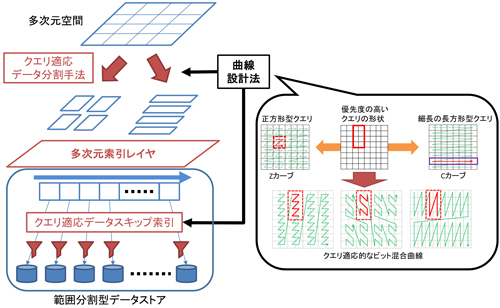
 本研究では，まずスケーラブルなデータ管理手法の一つであるデータの範囲による分割手法と多次元データを一次元データ化する空間充填曲線に着目し，範囲分割を工夫することで，伝統的な多次元索引であるkd-Treeと等価な機能を実現した．

 一方，データの管理単位であるページは複数のサーバに分散され，かつ，ページサイズが大きいため，ページのアクセスコストが大きく，その削減が高い性能を達成する上で重要である．一般的な方法として，クエリ実行時のページアクセス数を最小にするようなデータ分割の最適化や，クエリに関係するデータがページにない場合はアクセスをスキップする方法がある．前者は最適なデータ分割を求めることはNP困難であること，後者はデータ不在性の検査には空間使用量と偽陽性率にトレードオフがあり，特に多次元範囲の場合，両立が困難であることが知られている．

 これらの問題はどんな空間充填曲線を用いるかの曲線設計問題に帰着する．本論文では，応用上はクエリに優先度があること，また，属性ごとに典型的な集約の単位（時間であれば日，週，月）の存在に着目し，各属性の優先度が高い集約の単位に合わせたクエリ適応的な曲線設計手法を提案した．ここでは，正方形の形状のクエリに強いZカーブと，細長い長方形の形状のクエリに強いCカーブの構成上の類似点に注目し，これらを一般化したビット混合曲線族を提案，優先度の高いクエリの形状に合う曲線をその曲線族からヒューリスティックで導出する曲線設計法を開発した．この設計した曲線を用いることで，データ分割においてはアクセスするページ数を最大で１桁近く削減，データ不在性検査も空間使用量あたりの偽陽性率を最大で８倍改善した．

 これらの成果により，クエリに適応して効率的なスケーラブルな多次元索引手法を実現し，ビッグデータ時代におけるデータ管理に貢献した．