マーカレス3次元骨格位置推定のためのカメラキャリブレーション手法とバドミントン競技映像処理への実践
Camera Calibration for Markerless 3D Pose Estimation and Practice in Badminton Video Processing
1. はじめに
映像情報を用いた物体追跡処理は,コンピュータビジョンの重要な研究テーマとされている.特に,戦術分析を目的としたスポーツ競技映像における物体追跡処理に注目が集まっている[1].また体育学のバイオメカニクス分野において,選手の骨格位置を用いた研究事例が多く存在する[2].それらの研究では,選手を撮影した画像に,選手に装着したマーカ検出処理や目視判定処理を適用することで骨格情報を獲得している.しかし,マーカの観測を用いた手法には,マーカを装着せずに撮影した映像やセンサの計測範囲外では利用が困難となる問題が存在する.また,目視判定で骨格情報を取得する作業には,膨大な労力が必要となる.このような問題を背景として,スポーツ分野ではコンピュータを用いた骨格情報の自動的抽出の実現が求められている.
本研究では,様々なスポーツ競技を対象としたトレーニング支援を目的として,スポーツ競技映像から選手の骨格位置を検出するアルゴリズムの考案に取り組んでいる.2次元画像上の位置推定を目的として開発されたDeep Learningを活用した骨格位置検出アルゴリズムを拡張し,3次元骨格位置検出アルゴリズムを考案する.
これまでにも3次元追跡や3次元形状復元など多視点画像を用いた研究開発は盛んに行われている.特に大規模空間における被写体の3次元位置推定の研究は,多様なシーンを対象とした研究が進められている[3].これらの処理では3次元空間と2次元画像空間の射影関係を表すカメラパラメータが必要であり,カメラキャリブレーションを実施することでカメラパラメータを取得できる.カメラキャリブレーションはカメラ校正と同じ意味を表し,カメラ校正法には,強校正と弱校正がある.
強校正(人工的なランドマークを用いる手法)は,体育館のような大規模空間に設置された3次元ランドマーク座標と画像上の2次元ランドマーク座標を対応付けることで,カメラの位置・姿勢推定を行う.この手法は,体育館のような大規模空間にランドマークを万遍なく設置する必要があり多くの労力を必要とするが,高精度にカメラの位置・姿勢を推定することが可能である.一般的な強校正は,既知なランドマーク(チェッカーボード)を利用した手法が代表的である[4], [5].キャリブレーション精度向上を目的とした研究では,動的なシルエットからエピポーラ幾何を計算する方法[6]やカラーコードの活用[7]によって推定誤差を最小限に止めている.また,水中や医療内視鏡などのカメラキャリブレーションの困難な環境に対応した研究も報告されている[8], [9].これらはいずれも比較的小規模な空間を対象としている.空間中に3次元位置が既知なランドマークを設置し,画像上で観測される2次元位置との対応関係から射影変換行列を推定する強校正は最も基本的なカメラキャリブレーション処理の一つであるが[1],ランドマークの準備・設置作業が大規模空間に適用する場合の大きな問題である.このような問題を解決するために,虹を利用したカメラキャリブレーション手法が提案されている[10]が,虹は頻繁に出現するものではなく,屋内の大規模空間では適用が困難である.
弱校正(自然特徴点の対応関係を用いる手法)は,各画像上の共通な画像特徴点とカメラ間の対応関係から,射影幾何学を計算することによってカメラの位置姿勢を推定する手法である.強校正のようにランドマークを設置する必要はないが,カメラ間の画像特徴の正しい対応関係を計算する必要がある[11], [12], [13], [14].対応点を追加することによって,頑健なキャリブレーションを実現した例も報告されている[15]が,カメラが疎に配置されるなど,十分な対応点を得ることが困難な場合,推定精度が低下する問題が存在する.
このように,選手の3次元骨格位置を推定するためには,カメラキャリブレーションが必要である一方,我々が適用対象と考えている体育館などの大規模空間では,密にカメラを配置することが難しい場合が多く,疎に配置したカメラを高精度でキャリブレーションする手法の実現が望まれている.本稿では,図1に示すように疎な多視点カメラの間をモバイルカメラが移動しながら撮影した映像(補完画像)と多視点画像を統合することにより,疎に配置された固定カメラキャリブレーションを高精度かつ容易に実現する手法を提案し,その結果を用いたバドミントン選手の3次元骨格位置推定手法を紹介する.バドミントン競技の映像解析は,撮影時におけるコートサイズに特性がある.具体的には,バドミントンコートの大きさは,縦13.4 m,横6.1 mに設定されており,1台のカメラの画角に対して十分に収まる範囲となる.バドミントンコート全面が含まれるように撮影したときの人物の大きさは,観測される画像の10%程度の大きさであり,骨格を推定するために必要な十分な画素を保有している.一方で,サッカーコート全面(縦110 m,横75 m)が含まれるように撮影した場合の人物の大きさは,観測される画像の0.1%程度の大きさであり,骨格を推定するために必要な十分な画素を保有することができない.本研究を応用する場合は,カメラの台数を多くすることで応用が可能となる.このような競技特性の一例として本研究ではバドミントン競技を対象とする.
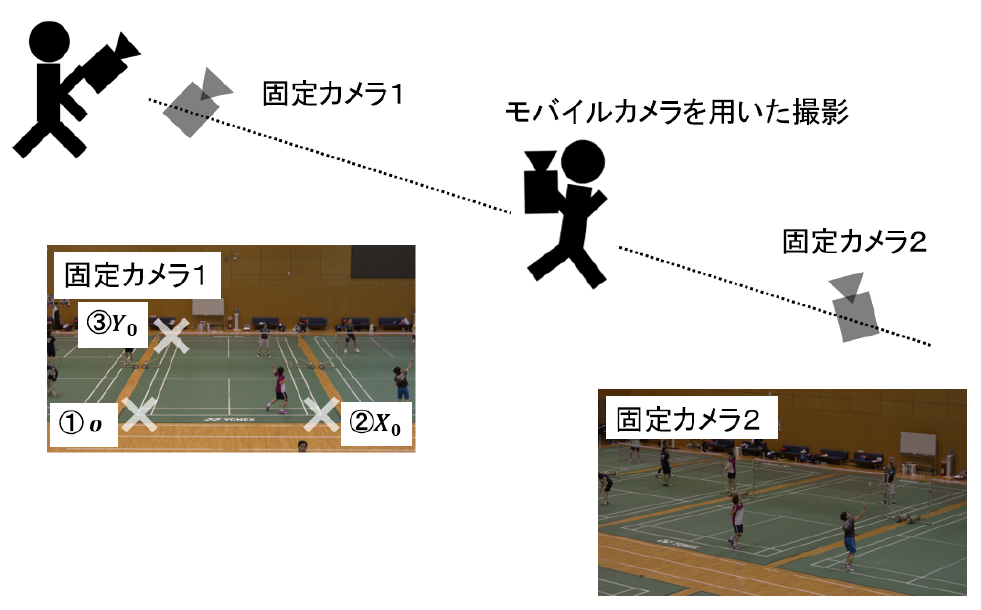
Fig. 1 Shooting method by the proposed method (a scene is captured while moving between sparsely arranged fixed cameras using a mobile camera).
以降,2章ではバドミントン競技空間におけるマーカレス3次元骨格位置推定法を提案し,3次元位置を推定するためのカメラキャリブレーション手法を提案する.さらに,従来手法の2次元骨格位置推定手法と提案するカメラキャリブレーション手法を組み合わせたスポーツ選手の3次元骨格位置推定手法を提案する.3章では多視点カメラキャリブレーション手法の精度評価実験および,多視点カメラキャリブレーションを利用したバドミントン選手の3次元骨格位置推定手法の精度評価実験について述べる.4章ではバドミントン競技映像処理における現場活用の可能性に向けて考察する.
2. バドミントン競技空間におけるマーカレス3次元骨格位置推定
2.1 多視点カメラキャリブレーション手法
本節では,バドミントン競技空間における3次元位置を推定するためのカメラキャリブレーション手法を提案する.図1に示すように,疎に配置した固定カメラによって複数視点画像を撮影する.同時に,固定カメラの間を固定カメラと同じ対象をとらえるようにモバイルカメラを移動させながらビデオを撮影する.ビデオをフレームに分割した補完画像と疎な多視点画像により,固定カメラを含む密な多視点画像群を獲得する.それらの画像群に対して弱校正を適用することにより,すべての多視点画像の射影変換行列を推定する.推定した射影変換行列から,疎な多視点画像に対応するものを抜き出すことにより,ランドマークを設置することなく疎に配置した固定カメラの高精度なカメラキャリブレーションを実現する.尚,推定精度を高めるためには,十分な対応点が検出される必要があることから,撮影空間中に画像特徴が検出されやすい物体が存在していることが提案手法適用の前提条件となる.たとえば,壁面にポスターを張る,バドミントンコート上に荷物を置く,などの工夫を撮影空間中に満遍なく実施することによって,十分な画像特徴が取得できる.本研究対象のような体育館の場合は,体育館内に存在する運動設備用品を置くと良い.また,弱校正はスケール不変であるため,大きさが既知の物体が撮影空間中に存在していることも条件となる.本研究ではバドミントンコートを利用している.
図2に示すように,任意の点の弱校正座標系における3次元座標を$M_{sfm} = [X_s, Y_s, Z_s, 1]^T$とし,それがカメラ座標系において$m = [u, v, 1]^T$で観測されている場合,弱校正座標系とカメラ座標系間の射影関係は,弱校正座標系におけるカメラの射影変換行列Pを用いて式(1)のように表される.\[\lambda m \simeq \boldsymbol{P} M_{sfm}\](1)
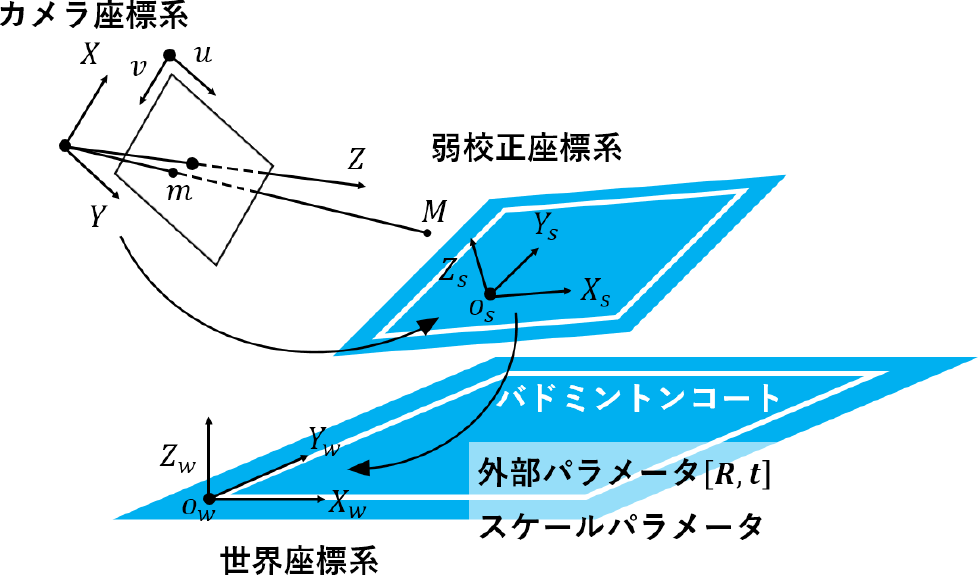
Fig. 2 Camera coordinate system, weak calibration coordinate system, geometric relations of world coordinate system.
$\lambda$はスケールファクタを表す.このとき,$M_{sfm}$はStructure From Motion [12]を用いることで取得できる.複数視点画像において同様に射影関係を推定し,それらの射影変換行列を用いたステレオ法により,画像上での観測座標からその3次元座標を算出する.図2および図4下段に示すように,各画像の対応点と射影変換行列を用いることで3次元位置を計算できる.弱校正座標系は,観測される対応点の分布に基づいて座標系が設定されるため,撮影ごとに原点や各軸の方向が変化してしまう.異なる撮影データにおいて統一的な計測を実現するために,撮影空間の世界座標系を設定し,弱校正座標系から世界座標系への変換を行う.世界座標系における任意の点を$M_{world} = [X_w, Y_w, Z_w]^T$とすると,弱校正座標系から世界座標系の変換は,式(2)に示すように,回転行列Rと並進ベクトルtを用いた剛体変換で表される.\[M_{world} = RM_{sfm} + t\](2)
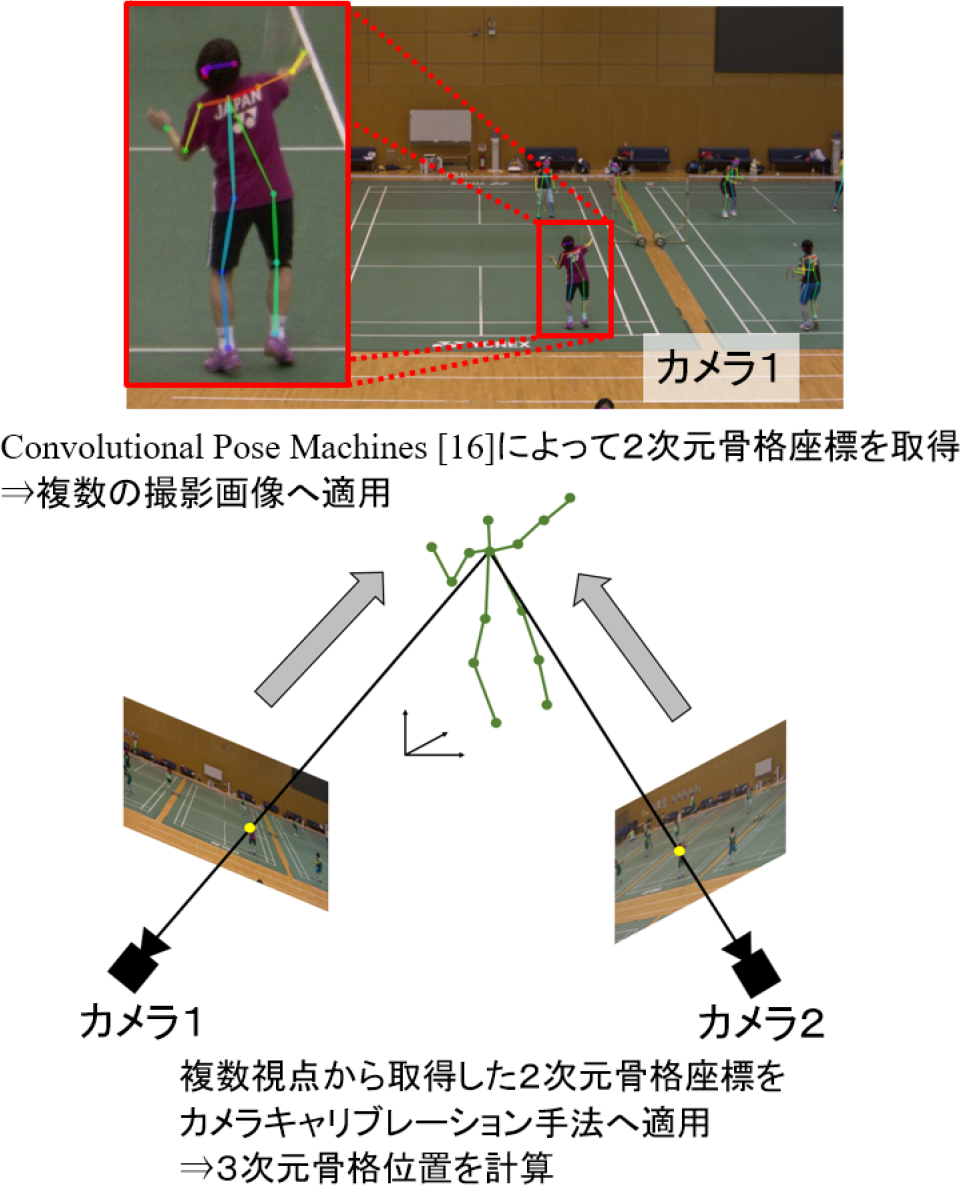
Fig. 4 3D skeleton estimation method for athletes by combining the 2D skeleton estimation method of the previous method and the camera calibration method.
ここで,3次元剛体変換行列Dは,\[D = \left[ \begin{array}{@{}cc@{}} R & t \\ 0 & 1 \end{array} \right]\](3)であり,\[\tilde{M}_{world} = D\tilde{M}_{sfm}\](4)と表され,式(4)を用いることで.弱校正座標系から世界座標系へ変換が実現される.
本研究では,図3に示すように,多視点映像の撮影シーンから,2本の直線(エッジ)が垂直に交わり,かつ,大きさが既知の物体が存在する領域を世界座標系の原点としている.ベクトルtは,世界座標系の原点に対応した弱校正座標系の点$S_o$から原点$o_{sfm}$への平行移動量として与えられる.また,スケールは,世界座標系で大きさが既知の物体を用いて,それに対応した弱校正座標系での大きさとの比によって求める.世界座標系のx,y,z軸上の点に対応した弱校正座標系における点$S_x$,$S_y$,$S_z$を用いて,式(5)によって表される弱校正座標系の正規直交基底ベクトルを算出し,各ベクトル$e_i$の成分から回転行列Rを求める.\[ e_i = \frac{S_i - S_0}{|S_i - S_0|}\ (i = x, y, z)\](5)
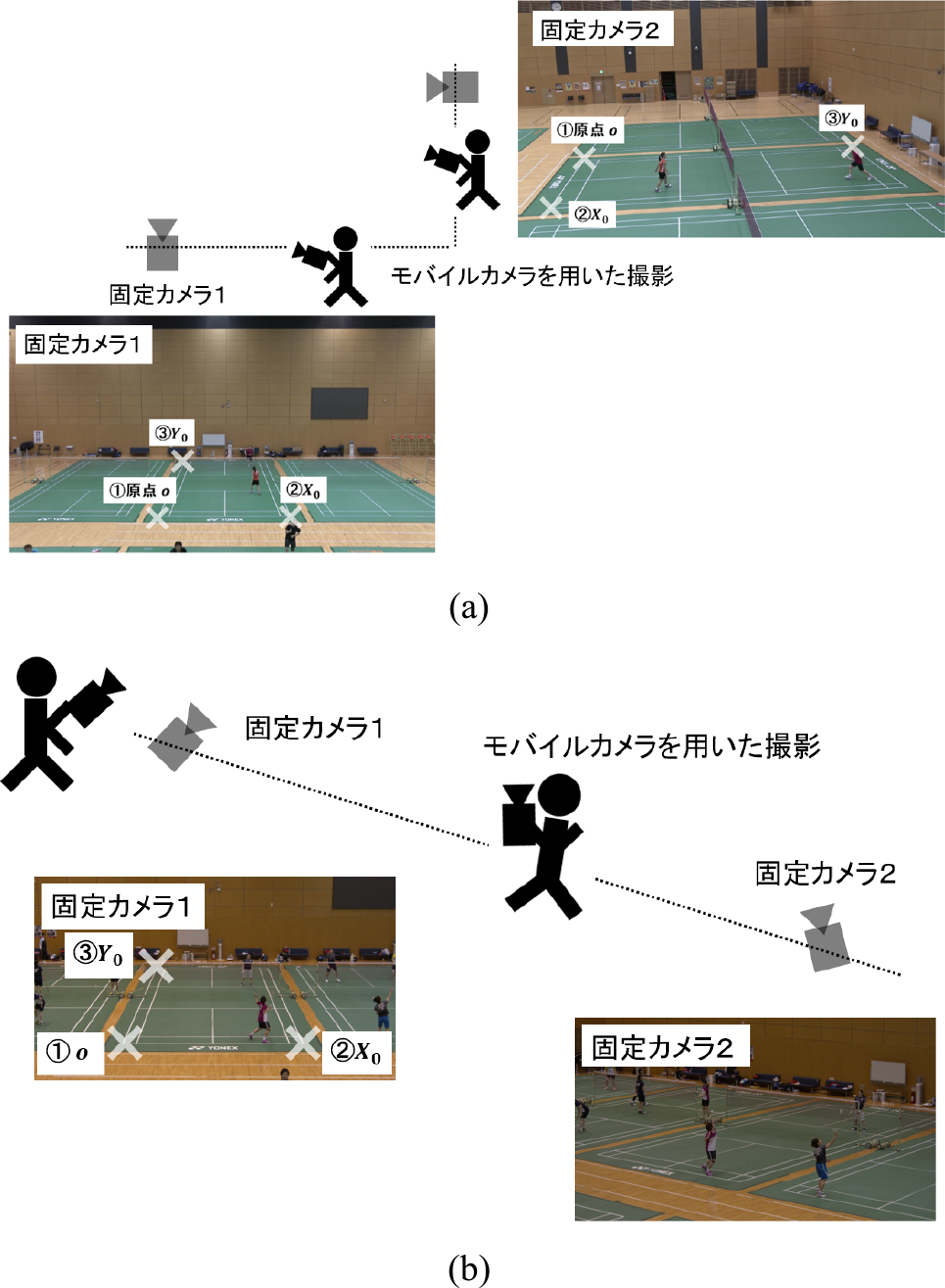
Fig. 3 Fixed camera layout design (a) Position of the origin o, X-axis, and Y-axis of the world coordinate system (distance between court and camera is approximately 20 m). (b) Two fixed cameras installed parallel to the X axis of the world coordinate system.
弱校正座標系から世界座標系へ変換することで,世界座標系における被写体の3次元位置を算出する.
上述したように弱校正(自然特徴点の対応関係を用いる手法)は,各画像上の共通な画像特徴点とカメラ間の対応関係から,射影幾何学を計算することによってカメラの位置姿勢を推定する手法である.したがって,図2に示すように弱校正座標系と世界座標系では座標系が異なる.弱校正座標系から世界座標系へ変換するためには,回転行列Rと並進ベクトルtを用いた剛体変換を実施する.このような変換を行うことで,バドミントンコートの任意の点を原点,縦横ラインをX軸Y軸と定義した世界座標系への変換を可能とする.この変換を実施しない場合,スケールが実世界と一致しない.スポーツのパフォーマンス分析をするうえでは実世界の計測が求められていることから,バドミントンコートラインの長さや選手の身長を実世界の長さと一致させるために必要な変換となる.
2.2 多視点カメラキャリブレーション手法を適用するための撮影方式
固定カメラの配置は,同じ対象物を撮影するように設置することが条件となる.さらに,モバイルカメラの撮影条件は,少なくとも固定カメラをつなぐ軌跡をたどるように同じ対象物を撮影することが条件となる.これは,提案手法で採用する弱校正では,画像特徴を手がかりとした隣接画像間の対応点情報に基づいてカメラのパラメータを推定するためである.このような撮影を実施することによって,固定カメラで撮影された画像とモバイルカメラで撮影された画像間の対応点情報が得られ,弱校正の適用が可能となる.したがって,提案手法では,固定カメラの配置方法として,図1や図3(b)のような配置だけでなく図3(a)のような配置も考えられる.モバイルカメラの撮影方法は,コートの中央方向に向けて移動しながらモバイルカメラの撮影角度を少しずつ変えて撮影する.1歩(約1 m)ごとに1枚の画像撮影が理想的であるが,カメラ間の距離が長い場合には多くの労力が必要となるため,モバイルカメラを用いた動画撮影を実施する.このときの撮影における設定は,手ぶれ補正機能を有効にし,比較的ゆっくりと歩行(普通歩行の約4 km/hより遅い約2 km/h程度)しながら撮影を行う.上述したとおり,弱校正を適用させるためには,隣接画像間の画像特徴の対応が必要となり,動きブレを多く含む画像に対しての画像特徴の対応を得ることは困難である.カメラの手ぶれ補正機能をオフにして撮影した映像や,比較的早い速度で歩きながら撮影した映像に対して弱校正処理を適用した場合,処理精度が低下することが懸念される.一方で,微小な手ぶれが生じる映像からは画像間の対応点情報を得ることができるため,弱校正が実行可能であり,キャリブレーション誤差も比較的軽微なものとなる.
2.3 多視点カメラキャリブレーションを利用したスポーツ選手の3次元骨格位置推定手法
本節では,従来手法の2次元骨格位置推定手法と2.1節で提案したカメラキャリブレーション手法を組み合わせたスポーツ選手の3次元骨格位置推定手法を提案する.応用事例の一つとしてバドミントン選手の姿勢推定を検討する.図4に示すように,複数の撮影画像に対して従来手法の2次元骨格推定手法であるConvolutional Pose Machines [16]を適用する.複数視点から取得した2次元骨格座標を2.1節で提案したカメラキャリブレーション手法へ適用する.したがって,複数視点から取得された2次元骨格座標は,弱校正座標系の3次元骨格位置へ変換され,実世界の世界座標系の3次元骨格位置へと変換される.
以上の提案手法によって推定された3次元骨格位置を図5に示す.推定された3次元骨格位置は,良好に3次元骨格位置が推定されていることが確認できるが,これは一例である.図3のようなカメラ配置の場合,横方向からの撮影映像ではセルフオクルージョンが頻発し,従来手法のConvolutional Pose Machines [16]を適用精度が低く,骨格を正しく推定されない.オクルージョンとは,3次元空間において手前にある物体が背後にある物体を隠して見えないようにする状態を表す.本研究におけるセルフオクルージョンとは,カメラの見え方によって選手の骨格の一部が選手自身の体によって隠れてしまう状態を表す.したがって,正しく推定されない骨格位置に対して,提案手法を活用した3次元骨格位置も正しく推定はされない.図5では図3(a)のようなカメラ配置において,従来手法のConvolutional Pose Machines [16]を適用した場合に正しく推定された一例を示している.従来手法のConvolutional Pose Machines [16]が正しく動作する場合に提案手法は効果的に作用する.
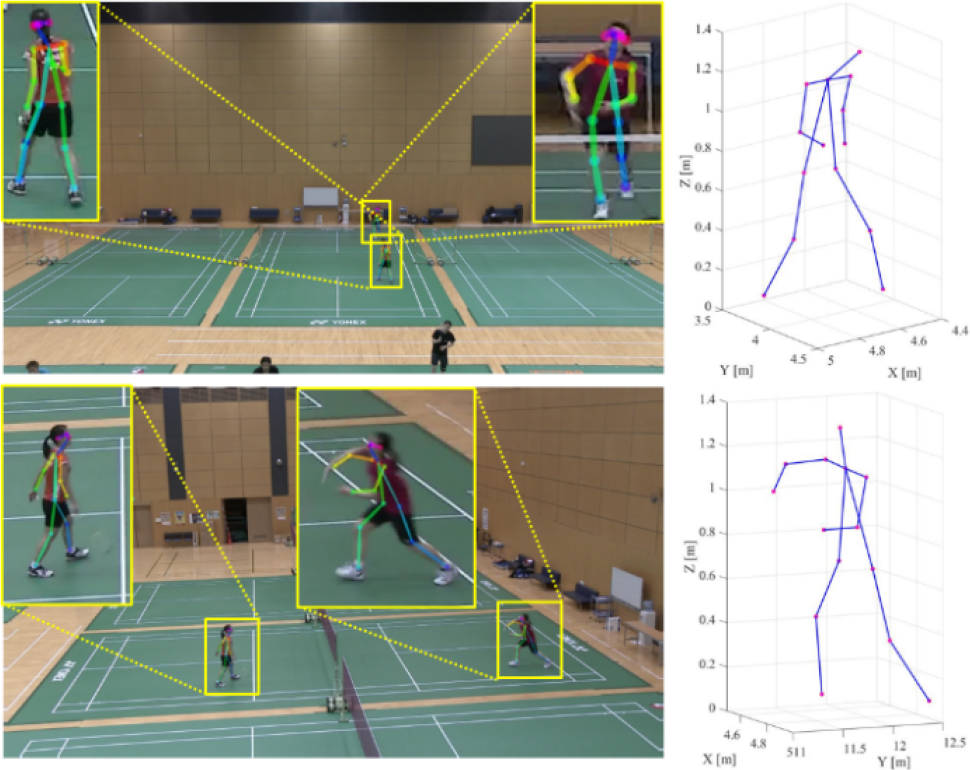
Fig. 5 3D skeleton position estimation results by the proposed method.
3. バドミントン競技空間におけるマーカレス3次元骨格位置推定法の評価実験
3.1 バドミントン競技空間における多視点カメラキャリブレーション手法の精度評価実験
本節では,多視点カメラキャリブレーション手法の精度評価実験について述べる.本実験では,モバイルカメラによる移動ビデオをフレームに分割した補完画像(フレーム分割の割合)を変化させることでキャリブレーション精度を検証し,3次元位置推定におけるキャリブレーション精度を担保できるフレーム分割の割合を明らかにする.
図3(a)に示すように,体育館においてバドミントンの練習風景を撮影し,光軸が世界座標系のX軸,Y軸と直交するように固定カメラを2台設置する.コートのコーナに原点,コートラインに沿ってX軸,Y軸が設定されている.競技規則上バドミントンコートラインは,図3の①②の距離が6.1 m,①③の距離が13.4 mと定められている.この値を用いてスケールパラメータを推定する.
多視点映像を撮影するカメラはソニー社FDR AX-1を用いた.横3840画素×縦2160画素の解像度の映像を毎秒30枚撮影する.また,同性能のカメラで二つの固定カメラ間を移動しながら同じ空間を撮影する.映像をフレームに分割することにより補完画像を取得する.
カメラキャリブレーションの精度を評価するために,移動撮影映像からフレームを切り出す間隔を調整し,300枚,150枚,75枚,40枚,20枚,10枚,5枚の補完画像を用意する.図6は,撮影した補完画像に対して弱校正処理を適用した結果を表す.図6上段は,カメラの移動経路に沿って撮影された補完画像群(300枚)から推定した各カメラの位置姿勢を表す.また,弱校正を適用した結果生成されるバドミントンコート上の空間の疎な3次元点群を表す.本研究では,弱校正によって生成される3次元点群は利用しないが,推定したカメラの位置姿勢を主観的に確認するために提示している.カメラの位置姿勢は,300個の四角錐で表され,カメラの移動経路と同等の軌跡がプロットされていることが確認できる.図6下段(a)–(g)は,撮影した補完画像枚数それぞれに対して弱校正処理を適用した結果を表す.図6上段と同じように補完画像枚数に対応するカメラの位置姿勢の推定結果が得られている.図6(a–g)のカメラの位置姿勢結果を順に観察すると,(a)では各カメラ位置が直線状に羅列されているが,補完画像の枚数を少なくするごとにカメラ位置姿勢が直線状に羅列されていないことが主観的に確認できる.これはカメラの位置姿勢が誤推定されている現象であり,このときのカメラキャリブレーション精度を検証するために次の客観的評価を実施した.
Fig. 6 Upper: Sparse 3D point cloud estimated from images captured along the camera movement path. And the position and pose of each camera. Bottom: (a)–(g) Results of applying weak calibration processing using the interpolation image acquired from the capture method in Fig. 3(a). (a: Interpolation images 300, b: 150, c: 75, d: 40, e: 20, f: 10, g: 5)
図6(a–g)に示すように,撮影した補完画像に対して弱校正処理を適用し,推定された固定カメラのパラメータを用いて,図3に示す世界座標系の原点①$o_{world}$,②$X_o$,③$Y_o$を算出する.比較対象として既知のバドミントンコート座標を用いて強校正処理を行う.競技規則上バドミントンコートラインは図7に示すように定められている.図3で定義した原点の位置を基準に世界座標系のコート座標およびポール先端位置(図7,No.1–18)を算出する.同様に,各画像上の指定した位置座標を取得し,強校正を行う.算出したカメラパラメータを用いて,図3に示す世界座標系の原点①$o_{world}$,②$X_o$,③$Y_o$を算出する.
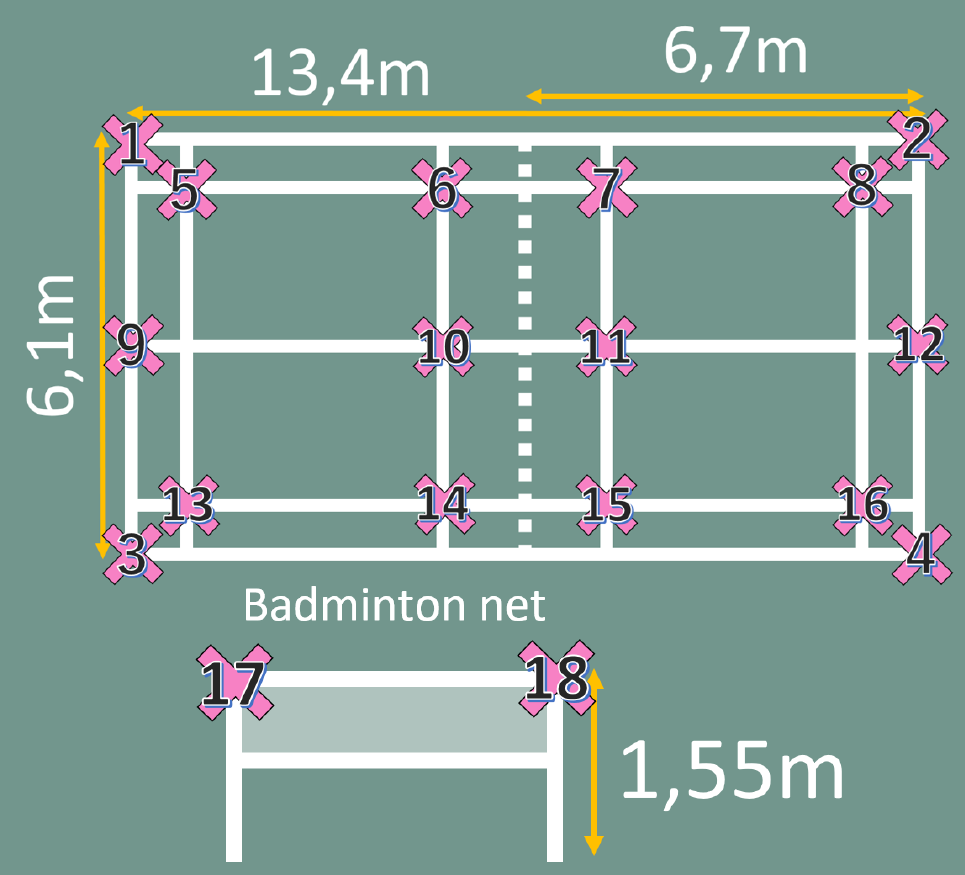
Fig. 7 Badminton court line distance and net height distance specified in the competition rules. Three-dimensional position used for strong calibration (No.1–18).
世界座標系の推定値(原点①$o_{world}$,②$X_o$,③$Y_o$)と競技規則で定められた値(①②6.1 m,①③13.4 mを用いた①②③の3次元位置)を比較する.②$X_o$,③$Y_o$と真値のユークリッド距離の算出誤差を図8に示す.バドミントンコート座標を用いた強校正による平均推定誤差は2.2 cm,最小値は300枚の補完画像を用いた場合で平均誤差値は4.3 cm,最大値は20枚の補完画像を用いた場合で平均誤差値229.5 cmであった.この結果から300枚の補完画像を用いた提案手法による平均推定誤差と,強校正による平均推定誤差の差は,2.1 cmであり,提案手法は,強校正とほぼ同等の精度であることを示している.一方で,少数枚の補完画像からの推定処理では世界座標系における誤差が大きい.補完画像300枚,150枚,75枚の場合は10 cm以下の誤差で3次元位置推定が可能であるが,補完画像が20枚を下回ると誤差が急激に増加する.図8の結果を確認すると補完画像40枚と20枚の平均誤差には大きな差がある.このときそれぞれの輻輳角は,補完画像40枚を用いた場合が約6度,補完画像20枚を用いた場合が約12度であった.輻輳角は,一つのカメラの対象物までの視線ともう一つのカメラの対象物までの視線を延長し,交差した角度を表す.対象物が正面にある場合,輻輳角は近くのものを見るときは大きくなり,遠くのものを見るときは小さくなる.この結果から,本手法を有効に機能させるためには,輻輳角が6度程度となるように補完画像を切り出すことが望ましい.たとえば,本実験環境では,図3(a)のカメラ間は約40 mである.この場合,秒速1 mの速度で歩行しながら撮影した映像を,毎秒1フレームで切り出すと輻輳角が6度程度の間隔で得られることになる.
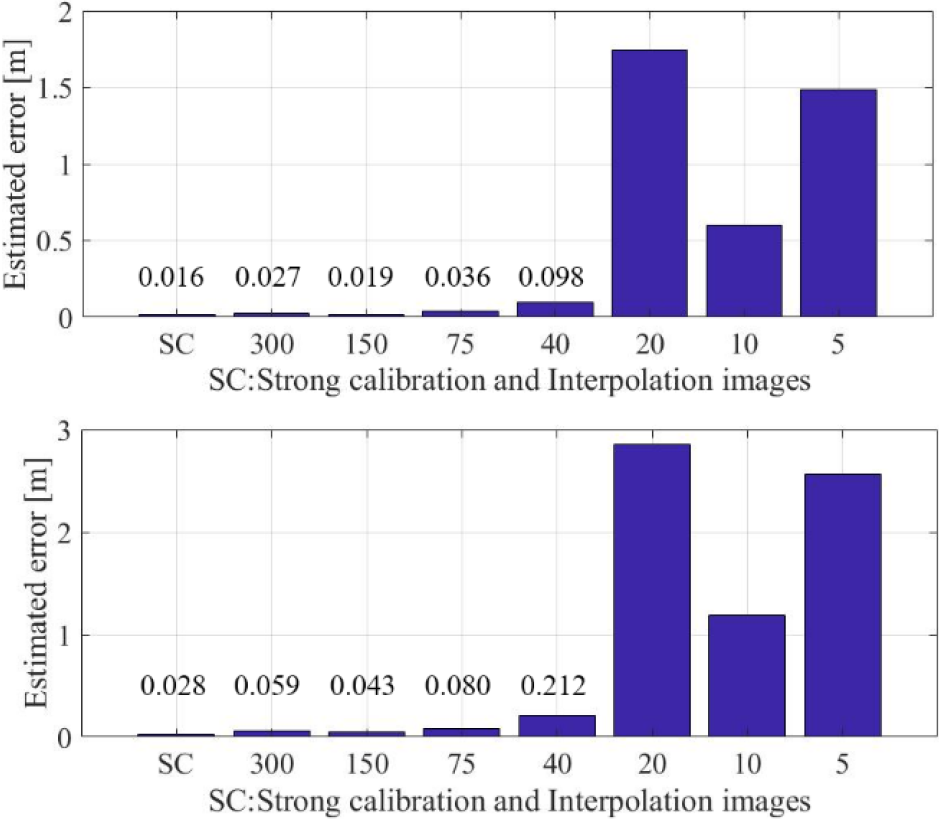
Fig. 8 ② Error of the result of calculating the Euclidean distance between $X_o$ (upper) and the true value. ③ Error of the result of calculating the Euclidean distance between $Y_o$ (bottom) and the true value.
3.2 多視点カメラキャリブレーションを利用したバドミントン選手の3次元骨格位置推定手法の精度評価実験
本節では,多視点カメラキャリブレーションを利用したバドミントン選手の3次元骨格位置推定手法の精度評価実験について述べる.本実験では,3次元骨格位置推定実験によって提案手法の適用範囲を明らかにする.
図3(a)のカメラ配置によって選手の3次元姿勢を良好に推定できたフレームは数フレームだけであった.この知見に基づき,図3(b)に示すように,2台のカメラから選手の背中が十分観測されるようカメラ配置を変更した.その結果,これまで課題とされていたConvolutional Pose Machines [16]の適用精度を向上させ,提案手法を活用した3次元骨格位置も良好に推定できることを以下に示す.特に着目しているのはショット動作の17フレームである.パフォーマンス分析に重要なシーンであるショット動作を良好に推定できること示すために,17フレームに焦点を当てる.尚,図3(a)のカメラ配置では,ショット動作のシーンにおける3次元位置推定は不可能であった.
推定した3次元骨格位置に対するカメラキャリブレーションの定量評価実験を実施した.この実験では,3次元キーポイントに注釈を付与することが難しいため,再投影誤差を評価した.この実験に使用されるバドミントンシーンは,シャトルコックの打撃開始から終了までの17フレームである.定量評価実験では初めに,図4に示すように,二つの視点からConvolutional Pose Machines [16]によって2次元座標を取得し,取得した二つの2次元座標を提案手法に適用し3次元骨格位置を計算する.このとき,提案手法を用いて3次元骨格位置を推定した結果を図10に示す.次に,図9上段に示すように,計算した3次元骨格位置から各カメラ画像上へ投影する.さらに図9下段に示すように,画像上へ投影された2視点の位置を,再び提案手法に適用し3次元骨格位置を計算する.最後に,図4に示すように最初に計算された3次元位置と図9に示すように再投影された3次元位置のユークリッド距離を計算し,再投影誤差を求めた.この計算結果を表1に示す.再投影誤差は,各部位ごとに17フレームの平均誤差を示す.表1に示すように,全体の再投影誤差の平均は,約2.72 mm,標準偏差の平均は0.81 mmであった.このように,提案手法によるカメラキャリブレーションは高精度であることを確認した.
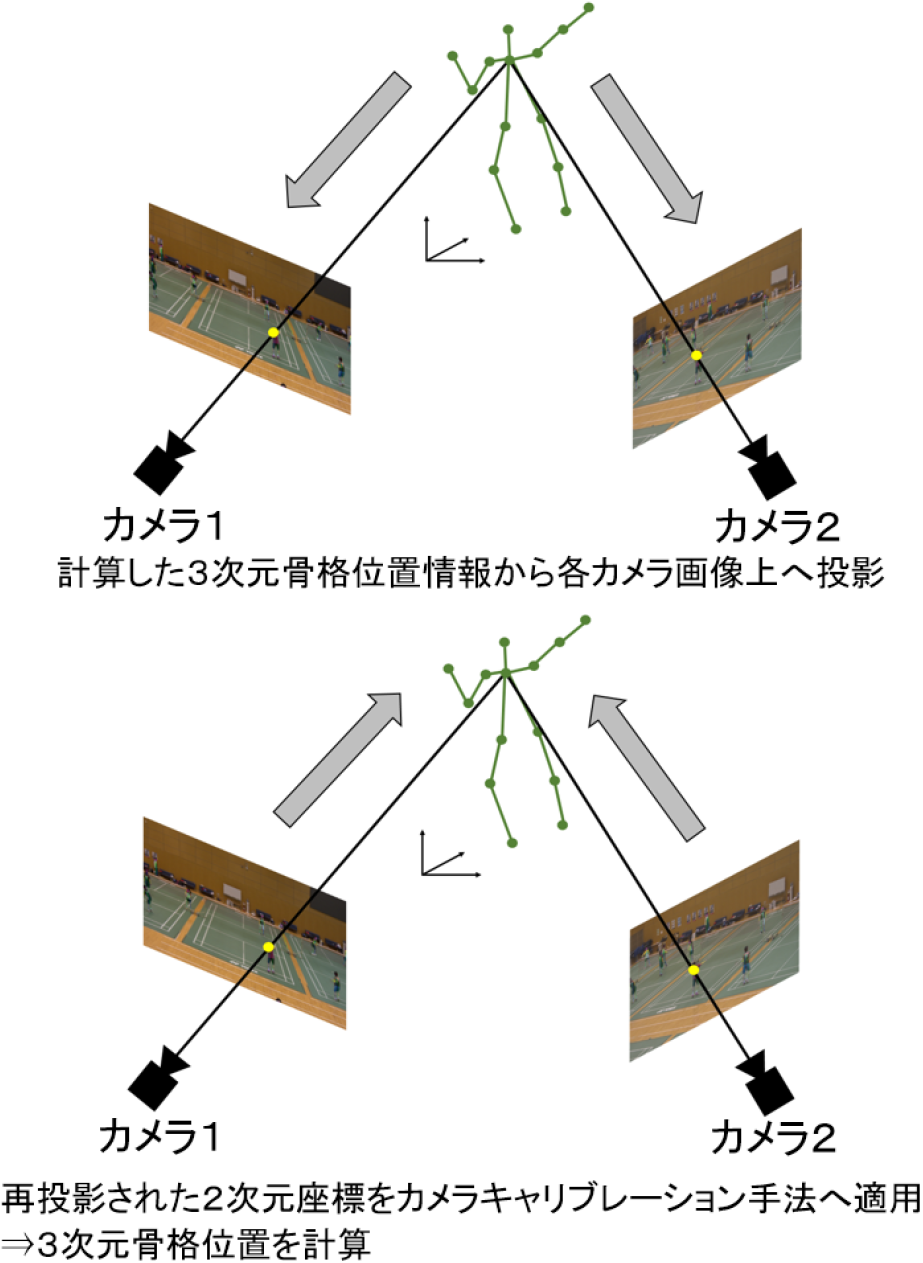
Fig. 9 Reprojection error comparison experiment (Upper: Projection from the calculated 3D skeleton position onto each camera image. Bottom: The positions of the two viewpoints projected on the image are applied to the proposed method again to calculate the 3D skeleton position.)
Table 1 Euclidean distance between calculated and reprojected 3D skeleton positions (reprojection error is averaged over 17 frames in each part of the skeleton).

上述した再投影誤差実験の手順3までに実行した結果を図11に示す.図11は,例としてフレーム123を示す.黄色の骨格線は,Convolutional Pose Machines [16]によって推定された2次元座標を示し,青色の骨格線は,一度,提案手法によって推定された3次元位置情報から,各カメラへ投影した2次元座標を示す.フレーム123では,骨格線が重なっていることが確認できる.しかしながら,選手の左肘から左手首の位置の骨格線は重なっていない.これは,選手のセルフオクルージョンが原因である.カメラ1の画像では,全身が観察できるが,カメラ2の画像では,左手が選手の体に隠れて観察できていない.Convolutional Pose Machines [16]は,セルフオクルージョンが存在しても骨格位置を推定するが,観察できない部位は推定精度が低い.したがって,Convolutional Pose Machines [16]の推定精度が低い部位では,提案手法による3次元位置の推定精度も低い.この問題を解決するためには,セルフオクルージョンが発生しないようなカメラ配置を検討しなければならない.
このように,従来手法によるConvolutional Pose Machines [16]と提案手法を組み合わせて推定した3次元骨格位置が,2次元画像上でどのように観察されるか,再投影することによって,その誤差を明らかにするために,再投影誤差を計算した.図9のように,提案手法にて推定された3次元骨格位置から各カメラに観測される画像上へ再投影することによって重畳された2次元骨格位置の比較が可能となり,再投影結果によって推定精度が低い骨格部位を明らかにした.
次に,手動8点の座標を用いたキャリブレーション手法と提案手法のキャリブレーション手法の定量評価実験を実施した.8点キャリブレーション手法では,図7に示す,点1,2,3,10,11,16,17,18の画像上の位置を手動で取得し,3次元フィールドとの8点の対応関係よりカメラパラメータを算出した.定量評価実験に使用するデータは,図12下段(赤色プロット)に示すように,選手のショット映像からラケットの位置を手動で取得した(21フレーム).図12におけるシーン(21フレーム)は,ショット動作の一部である.ラケットの位置がコート平面に対して垂直方向へ移動しているシーンである.このようなシーンを評価することによって,コート平面に対して垂直方向へのキャリブレーション精度を評価することができる.8点校正方法では,コートの情報(平面)を利用していることからコート平面に対して,垂直方向のキャリブレーション精度を検証する.
Fig. 12 Quantitative evaluation of the proposed method and the 8-point calibration method. Upper: Results of racket length estimation using the proposed method and the 8-point calibration method. Lower: Racket position (21 frames) obtained manually from player images.
2視点で取得したラケットのトップとアンダーの位置から8点キャリブレーション手法を適用し3次元位置を算出することでラケットの長さを算出する.同様に,2視点で取得したラケットのトップとアンダーの位置から提案手法を適用し,ラケットの長さを算出する.ラケットの実寸は674 mmである.ラケットの長さを推定した結果を図12上段に示す.8点キャリブレーション手法は青プロット,提案手法はオレンジプロットで示される.
実験の結果,両方の手法ともにラケットの長さの推定誤差平均は,8点キャリブレーション手法が12.69 mm,提案手法が11.86 mmでありほぼ変化はなかった.一方で,1フレームから10フレームまでの推定したラケットの長さの標準偏差を比較すると,8点キャリブレーション手法が6.21 mm,提案手法が6.27 mmであった.
11フレームから21フレームまでの推定したラケットの長さの標準偏差を比較すると,8点キャリブレーション手法が12.30 mm,提案手法が8.47 mmであった.この結果は,1フレームから10フレームまでの推定誤差に手法の比較による変化はみられないが,11フレームから21フレームまでの推定誤差は提案手法のばらつきが少ない結果を表している.1フレームから10フレームまでのシーンにおいてラケットの高さはコートネットの高さより低く,11フレームから21フレームまでシーンにおいてラケットの高さはコートネットの高さより高い.したがって,8点キャリブレーション手法はコートネットの高さより高い位置のキャリブレーション精度は不安定である.一方で,提案手法は,コートネットの高さより高い位置であってもキャリブレーション精度は安定している.この安定する要因は,3次元空間に万遍なく分布している画像特徴を提案手法は使用していることである.したがって,提案手法は,世界座標系の高さ方向のキャリブレーション精度も安定する.
4. バドミントン競技映像処理における現場活用の可能性に向けて実践から得られた知見と今後の課題
3次元骨格位置を推定するためには少なくともカメラを2台設置しなければならなく,カメラ台数を増加するほど,高精度に3次元位置推定を実現できる.一方で,公式試合におけるカメラ配置が可能な範囲は制限されている.図13左に示すようにごくわずかな領域でも2台以上のカメラが設置可能であれば,前章で紹介した実験のように適用できるが,カメラ間隔が近いため奥行きの推定精度の低下が懸念される.このようにカメラ台数の増減や配置によって3次元位置の推定精度は変化する.本章では,前章で紹介した実験に基づくバドミントン競技特性,カメラ配置の検討,現場環境の問題点,2次元骨格推定手法の利活用の課題について考察する.
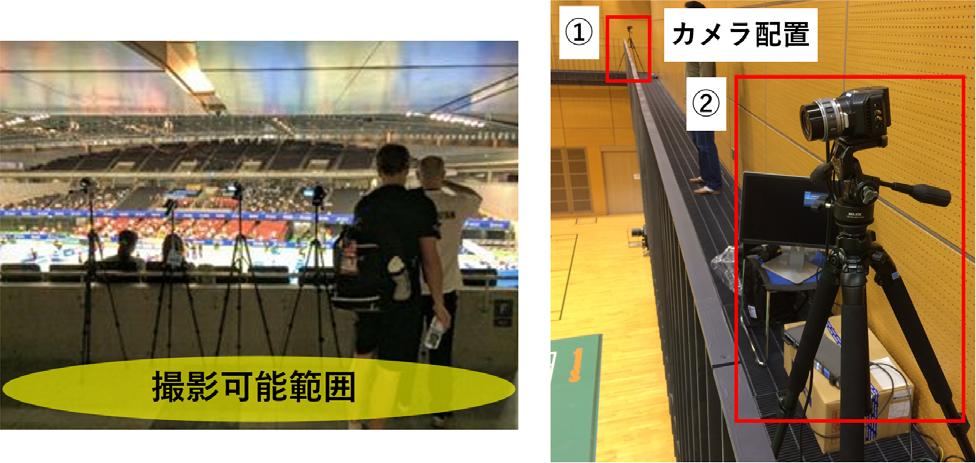
Fig. 13 Left: The range where cameras can be placed in the official badminton game. Right: An example of placing a camera in a gym for badminton practice.
バドミントン競技はネットで区切られているスポーツでありプレイヤーの数が少ないため,映像中に選手が重なり合うようなシーンが比較的少ない特性がある.柔道などのスポーツでは,選手同士が常に重なり合っていることから選手の骨格推定を妨げる要因が多々存在する.その反面,テニス競技では,ネットで区切られているスポーツでありプレイヤーの数が少ない類似性があり,本研究の応用が期待できる.さらにバドミントン競技は屋内スポーツであり,カメラを容易に設置できる利点がある.バドミントン競技の撮影映像は,ほぼ同じアングルから撮影されていることが多く,様々な会場で撮影された映像について同様の議論が成り立つ.
次にカメラ配置について実践から得られた知見を述べる.提案手法の有効性を検証するために,図3(a)に示すカメラ配置を実施した.この配置は3次元位置推定誤差を極力低減させるために検討した配置であるが,選手の骨格位置推定においてセルフオクルージョンが頻発する課題があった.この問題を解決するために次回の検証実験では,図3(b)に示すようなカメラ配置を実施した.このときの実験環境を,図13右に示す.カメラ間隔は約20 mである.このとき撮影された固定カメラの様子を図3(b)に示す.コート背面と斜め方向にカメラを配置した映像に対して提案手法を適用し,バドミントン選手の3次元骨格位置を算出すると,図10に示すような3次元骨格位置となる.上述したようにセルフオクルージョンの発生が懸念されるが,選手の右半身は比較的安定して3次元骨格位置を推定できることが分かった.したがって,前回の実験のカメラ配置において課題とされていたセルフオクルージョンが頻発する課題を図3(b)に示すカメラ配置へ変更することで右半身のセルフオクルージョンの課題を解決した.これらのことから,斜めに配置したカメラと対称の位置にもう1台斜めにカメラを配置すると全身の3次元骨格位置を安定して推定することが可能になると考えられる.たとえば,カメラを3台配置し,中央と左斜めのカメラを用いて左半身の骨格位置を推定し,中央と右斜めのカメラを用いて右半身の骨格位置を推定し,両結果を結合することによって,3次元骨格位置の安定な推定を可能とする.
公式試合の環境では上述したようなカメラ配置は現実的ではなく,提案手法は練習時のようなカメラ配置が自由に行える体育館に適している.一方で,複数回長期間にわたる実証実験のすべての環境(詳細は後述する)において,2台のカメラを用いた3次元骨格位置推定で安定して取得できる骨格位置は首であった.首は自身の肩によるセルフオクルージョンが発生するが肩-首-肩とカメラの光軸上に並んでいることから,セルフオクルージョンの影響は少ないことが確認されている.したがって,選手の3次元移動距離や動作速度などの情報取得を目的とする場合は,首の位置情報を利用することで正確な計測が可能である.
以上の考察より,2台のカメラを用いた場合,首の位置や骨格の重心を安定して推定できることから選手位置1か所の移動速度やフットワークの軌跡を用いた分析に活用できる.一方で,3台のカメラを用いた場合,全身の骨格位置を安定して推定できることから,選手の全身の骨格位置におけるバイオメカニクスと動作分析に活用できる.このように,カメラ配置が可能な台数に応じて推定されたデータを分析の種類ごとに使い分けることが可能である.
現場活用の懸念事項として,体育館の揺れの問題が挙げられる.体育館の地面にカメラを配置した場合,競技中の選手の振動により地面は揺れる.また,観客席においても通行人の振動の影響がある.したがって,カメラが揺れることで撮影映像は動きブレを含み,カメラキャリブレーション精度が担保されない.映像分析に有効な撮影を実施するためには,十分な範囲のカメラ配置領域の確保と,カメラを守る人的コストが必要である.実際に撮影実験を実施することによって得られたこのような知見を活かし,図13左に示すバドミントン世界大会の撮影実験では,カメラと観客の接触を避けるためのカメラを守る人を配置した.図13右に示す練習時の体育館における撮影実験では,スロープの揺れを低減させるために,撮影の操作はリモートで行い,撮影中に人がスロープに入ることはないように心がけた.
このように3台の固定カメラ配置計画,安定して推定される首の3次元位置,体育館の揺れ対策は実践から得られた知見である.
本研究では,Convolutional Pose Machines [16]を用いた3次元骨格位置推定手法を提案した.Convolutional Pose Machines(以下,Open Pose)では,プログラムの更新が現在までに複数行われ,推定精度が向上している.スポーツ映像処理によるパフォーマンス分析では,継続した動作計測が盛んに行われているが,Open Poseのプログラムを更新すると,これまでの計測結果と比較する場合にシステムの精度が向上したのか選手のパフォーマンが向上したのか判断が難しい問題が顕在化する.したがってスポーツ映像処理によるパフォーマンス分析では,頻繁にプログラムを更新することは推奨し難い.更新プログラムを適用する場合は,一定期間の測定を旧新プログラムの双方で実施し,プログラムを変更したことによるパフォーマンス分析の変化を把握したうえでの,切り替えが推奨される.
競技指導者などの現場の声として,次のような意見をいただいた.
- ・マーカレスで選手の3次元動作を計測できる技術は需要があるが,カメラキャリブレーションの煩雑な作業を競技指導者が実施するのは困難
- ・理想は1クリックで動作が完了するシステム
- ・このようなシステムから計測される3次元動作は,選手のパフォーマンス分析に役立つ
- ・競技指導者による選手分析は主観であり,そのエビデンスとして活用できる
- ・アーカイブとしての活用(過去,現在のパフォーマンス比較分析)
これらの意見に対して,提案システムは,ユーザが選手パフォーマンスを分析するためのデータを計測できるが,ユーザ自身が容易に使えるシステムまでは構築されていない.競技指導者などの現場の方へ容易に利用していただく方法の一つとしては,提案撮影システムを体育館へ常設することである.しかし,体育館への常設はコストの問題や許可の問題が存在する.移動式撮影システムでは補完画像を撮影するだけでカメラキャリブレーションを実現できるが,現場の方へ1クリックで利用できるほど容易なシステムではない.したがって,ほとんどの作業を自動化することが必要となる.様々な体育館の環境により微調整が必要になることも予想できる.1クリックで動作が完了するシステムでは,システム構築時に想定した以外の事象に対する対応ができない.したがって,ユーザの作業を支援できる自動化システムを考案することで解決を図る.提案システムでは,パフォーマンス分析のエビデンスとして活用できる要素があることから,より安定した計測精度が今後の課題となる.またパフォーマンス分析に活用されている骨格以外の情報について探索し,計測の実現を目指す.
尚,本章における考察・知見は,3か所の総合体育館や競技場でバドミントン競技を撮影した実証実験から得られたものであり,1回の撮影実験によって取得されたデータを数か月間検証し,次の撮影実験を実施している.したがって3か所の体育館に対して2回ずつ撮影実験を実施し,期間は約2年を要した.
5. おわりに
本研究では,バドミントン競技空間におけるマーカレス3次元骨格位置推定法を提案し,3次元位置を推定するためのカメラキャリブレーション手法を提案した.さらに,従来手法の2次元骨格位置推定手法と提案するカメラキャリブレーション手法を組み合わせたスポーツ選手の3次元骨格位置推定手法を提案した.多視点カメラキャリブレーション手法の精度評価実験の結果,モバイルカメラによる移動ビデオをフレームに分割した補完画像(フレーム分割の割合)は,輻輳角が6度程度の間隔になるように分割すると安定したキャリブレーション精度が担保できることを確認した.多視点カメラキャリブレーションを利用したバドミントン選手の3次元骨格位置推定手法の精度評価実験を実施し,提案手法の適用範囲を明らかにした.
本研究はJSPS科研費17K13180およびJST,CREST JPMJCR16E3の助成を受けたものである.
参考文献
- [1] 宍戸英彦,北原 格,亀田能成,大田友一:モーションブラーを活用したバドミントンシャトル追跡手法,電子情報通信学会論文誌D, Vol.J98-D, No.7, pp.1083–1097 (2015)
- [2] Jinji, T., Ohta, K., and Ozaki, H.: Multi-body power analysis of the baseball pitching based on a double pendulum, Procedia Engineering, Vol.34, (2012)
- [3] Xu, Y., Liu, X., Liu, Y. and Zhu, S.-C.: “Multi-View People Tracking via Hierarchical Trajectory Composition,” Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.4256–4265, 2016.
- [4] Scaramuzza, D., Martinelli, A. and Siegwart, R.: A Flexible Technique for Accurate Omnidirectional Camera Calibration and Structure from Motion, Proc. Fourth IEEE International Conference on Computer Vision Systems (ICVS'06), pp.45–45 (2006)
- [5] Chen, X. and Yang, Y. H.: Two-View Camera Housing Parameters Calibration for Multi-layer Flat Refractive Interface, Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.524–531 (2014)
- [6] Ben-Artzi, G., Kasten, Y., Peleg, S. and Werman M.: Camera Calibration From Dynamic Silhouettes Using Motion Barcodes, Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.4095–4103 (2016)
- [7] Schillebeeckx, I. and Pless, R.: Single Image Camera Calibration with Lenticular Arrays for Augmented Reality, Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.3290–3298 (2016)
- [8] Nishimura, M., Nobuhara, S., Matsuyama, T., Shimizu, S. and Fujii, K.: A Linear Generalized Camera Calibration From Three Intersecting Reference Planes, Proc. The IEEE International Conference on Computer Vision (ICCV), pp.2354–2362 (2015)
- [9] Melo, R., Barreto, J. P. and Falcao G.: A New Solution for Camera Calibration and Real-Time Image Distortion Correction in Medical Endoscopy-Initial Technical Evaluation, Proc. IEEE Transactions on Biomedical Engineering, Vol.59, No.3, pp.634–644 (2012)
- [10] Scott WorkmanRadu, Paul Mihail and Nathan Jacobs, “A Pot of Gold: Rainbows as a Calibration Cue,” Proc. European Conference on Computer Vision (ECCV), pp 820–835, 2014.
- [11] 金谷健一,三島 等:未校正カメラによる2画像からの3次元復元とその信頼性評価,情報処理学会論文誌,コンピュータビジョンとイメージメディア,Vol.42, No.SIG 6 (CVIM 2), pp.1–8 (2001)
- [12] Wu, C.: Towards Linear-Time Incremental Structure from Motion, Proc. 2013 International Conference on 3D Vision - 3DV 2013, pp.127–134 (2013)
- [13] Wu, C.: Critical Configurations for Radial Distortion Self-Calibration, Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.25–32 (2014)
- [14] Wilson, K. and Snavely, N.: Network Principles for SfM: Disambiguating Repeated Structures with Local Context, Proc. The IEEE International Conference on Computer Vision (ICCV), pp.513–520 (2013)
- [15] Cohen, A., Sattler, T. and Pollefeys, M.: Merging the Unmatchable: Stitching Visually Disconnected SfM Models, Proc. The IEEE International Conference on Computer Vision (ICCV), pp.2129–2137 (2015)
- [16] Wei, S.-E., Ramakrishna, V., Kanade, T. and Sheikh, Y.: Convolutional Pose Machines, Proc. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp.4724–4732 (2016)

宍戸 英彦(正会員)shishido@ccs.tsukuba.ac.jp
2016年,筑波大学大学院システム情報工学研究科修了.同年,(独)国立スポーツ科学センター研究員を経て,2017年より筑波大学計算科学研究センター助教,2018年,英国サリー大学客員研究員.コンピュータビジョン,多視点映像解析の研究に従事.博士(工学).

北原 格(正会員)kitahara@ccs.tsukuba.ac.jp
1996年筑波大学大学院理工学研究科修了.同年シャープ(株)入社.2000年筑波大学先端学際領域研究センター助手,2003年(株)国際電気通信基礎技術研究所(ATR)研究員,2005年筑波大学大学院システム情報工学研究科講師,2008年同准教授を経て,2019年より同大学計算科学研究センター教授.自由視点映像,複合現実感の研究に従事.博士(工学).
再受付日 2020年6月1日/2020年7月13日
採録日 2020年08月03日
![左:撮影画像にConvolutional Pose Machines [16]を適用した結果 右:検出した2次元骨格情報から推定される3次元骨格位置と軌跡 Left: Result of applying Convolutional Pose Machines [16] to the captured image. Right: 3D skeleton position and trajectory estimated from detected 2D skeleton information.](1-1-5-10.png)
![Convolutional Pose Machines [16]および提案手法にて推定された3次元骨格位置から各カメラに投影することによって重畳された2次元骨格位置 2D skeleton position overlapped by projecting to each camera from 3D skeleton position estimated by Convolutional Pose Machines [16] and the proposed method.](1-1-5-12.png)