Canonical Decompositions Describing Structures of Matchings in Graphs

 近年WWWやバイオインフォマティクスなどの台頭に伴い、ネットワーク構造を扱うさまざまな分野におけるデータの巨大化および解くべき問題の多様化が加速している。したがって、より効率のよいアルゴリズムをより汎用性の高い手法で設計することがグラフアルゴリズムの分野における逼迫した課題となっている。効率のよいアルゴリズム設計にはグラフの構造を精査しキーオブザベーションを得ることが必須である。これに際してはグラフの種々の分解定理が強力で汎用的な性格を持つツールとなる。そのようなグラフの分解として本研究では特に総称して「標準分解」と呼ばれる一連の分解定理に注目した。偶奇性の本質をうまく捉えるグラフ理論的概念としてマッチングが知られており離散数学の黎明期より盛んに研究されてきたが、標準分解はマッチングの概念を軸に与えられる分解である。既知の標準分解はいずれもマッチングの研究のみならず、最短パスをはじめとする種々の経路問題や行列計算など多岐に渡りツールとして活用されてきた。

 本研究の貢献は以下のようである。

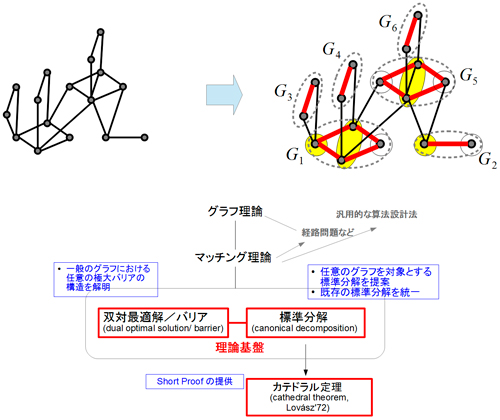
（1）任意のグラフを適用対象し、既知の標準分解をまとめ上げる新しい標準分解の提案
 これまで標準分解としてGallai-Edmonds 分解（Gallai'64, Edmonds'65）をはじめとする3つの分解がしられてきたが、いずれも特殊なグラフのみを適用対象とする、あるいは分解が粗く十分な情報を与えない場合があるなど欠点があった。また、これらの互いの論理関係なども不明であった。これに対し、本研究では任意のグラフを適用対象とし、かつ既知のものの一般化や細分を与える新しい標準分解を提案した。これにより既存の標準分解3つをまとめ上げ統一的に理解することが可能になった。これで以て標準分解の理論は約40年の空白期間を経て一通り完成に至ったと言える。

 さらに、新しく提案した標準分解を用いることで以下のような成果を得た。

（2）グラフの極大バリアの構造の解明
 バリアとは最大マッチング問題の双対最適解に相当する概念であり、すなわちマッチングと対を成す概念である。しかしバリアの構造の解明は難しく、これまで特に一般のグラフにおける大きな成果は特にしられていなかった。本研究では、一般のグラフにおけるバリアの構造を明らかにした。

（3）マッチングの数え上げ問題に対する貢献
 完全マッチングの数え上げは数え上げ組合せ論における代表的な問題である。本研究ではグラフパラメタと完全マッチングの総数の関係を調べるのに有用であるCathedral Theorem（Lovasz '72）の短証明を与えた。

 最大マッチング問題は多項式時間可解クラスの中核に座し離散最適化における最も重要な問題であると位置づけられている。事実、離散最適化問題の統一的な理論である多面体的組合せ論は最大マッチング問題をモデル問題として理論体系が組立られており、標準分解はその礎となっている。本研究はこのような観点においても今後アルゴリズム設計の理論体系への貢献が期待できる成果である。